Integrais: O que é, como calcular e suas aplicações

Integrais
Teoria
27/03/2025
Daniel Duarte

Completando a tríade de assuntos que constituem a base do cálculo, a integral é um conteúdo abrangente e com contribuições importantíssimas para o estudo das funções. Ao longo deste artigo, tentarei explicar de forma simples o que é a integral, quais os métodos de integração que existem e suas aplicações mais relevantes.

O que é a integral?

Assim como a potenciação é a operação inversa da radiciação, como a multiplicação é o inverso da divisão, a integral, também conhecida como antiderivada, é a operação inversa da derivada, ou seja, ao integrarmos uma função que foi derivada, obtemos a “função original”, anulando assim a derivada que foi aplicada anteriormente nela. E o contrário também é verdade, se derivarmos uma função que foi integrada, obteremos a função antes de ser integrada. A integral de uma função é representada pela simbologia abaixo:

$\int f (x) d x = F (x) + C$

O $\int$ indica que está sendo realizada a operação de integração, e a função $f (x)$ que está sendo integrada se chama “integrando”. O $d x$ (diferencial) nos informa a variável de integração (analogamente a derivada, onde derivamos uma função em relação a uma variável independente, na integral acontece algo similar, precisamos determinar a variável pela qual estamos integrando a função). Já o $F (x)$ é chamado de “primitiva” da função $f (x)$ , ou seja, é a função que ao ser derivada, se torna $f (x)$ , podemos interpretar como se a função $f (x)$ fosse a derivada de uma outra função $g (x)$ , e ao calcularmos a integral, descobrimos quem é a função $g (x)$ . Tente lembrar que a palavra “primitivo” significa o que veio primeiro, a origem de algo, e nesse caso, ao acharmos a integral, estamos encontrando “a função que veio antes da derivada”. O $C$ representa uma constante qualquer, mas ele merece uma atenção especial, que será dada no próximo tópico.

A integral é classificada de duas formas, ela pode ser “indefinida” ou “definida”, no primeiro caso, teremos como resposta uma função (um conjunto de funções, para ser preciso, como você logo verá), e no segundo, acharemos um valor numérico finito como resultado. Vale ressaltar que a integral não é somente isso, mas a princípio, essa informação será suficiente para começarmos a entender o assunto.

Como calcular uma integral indefinida?

Para resolvermos uma integral indefinida, devemos fazer a seguinte pergunta: “Qual função que ao ser derivada, resulta no integrando?”, vamos ver um exemplo para que fique mais claro.

Exemplo 1: Calcule a integral da função abaixo:

$\int c o s (x) d x$

A função que está sendo integrada é $c o s (x)$ (que é o nosso integrando). Calcular a integral indefinida dessa função é descobrir qual função que ao derivarmos, chegamos em $c o s (x)$ , e para determinar isso é importantíssimo que saibas a tabela de derivadas. A função cuja derivada é $c o s (x)$ é a função $s e n (x)$ , portanto, a primitiva de $f (x) = c o s (x)$ , é $F (x) = s e n (x)$ .

$\int f (x) d x = F (x) + C$

$\int c o s (x) d x = s e n (x) + C$

Alguns devem estar se perguntando o significado desse “C” no resultado da integral, de forma simplificada, ele indica que qualquer função que tiver $s e n (x)$ somado a uma constante vai resultar em $c o s (x)$ ao ser derivada. Vamos observar as funções abaixo e suas derivadas:

$f (x) = s e n (x) + 3$

$f^{'} (x) = c o s (x)$

$g (x) = s e n (x) - 7$

$g^{'} (x) = c o s (x)$

$h (x) = s e n (x) + π$

$g^{'} (x) = c o s (x)$

Independentemente da constante que estava sendo somada ao $s e n (x)$ , o resultado da derivada foi o mesmo, para as três funções distintas. Isso ocorre, pois a derivada de uma constante é zero, então, para contemplar todas as possíveis funções que tenham a derivada igual a $c o s (x)$ , acrescenta-se o $+ C$ .

A não ser que a questão nos dê uma informação adicional para que consigamos achar o valor dessa constante e determinar uma única função como resposta da integral indefinida, o resultado que obtemos ( $F (x) + C$ ), representa uma família de funções que podem ser primitivas do integrando.

Exemplo 2: Encontre a primitiva da função abaixo, sabendo que $F (0) = 3$ .

$\int e^{x} d x$

Caso não saibas de cara a resposta da integral, recomendo que faça a si mesmo a pergunta:”Qual função que ao ser derivada, resulta em $e^{x}$ ”, nesse caso, é a função $e^{x}$ , pois derivando $e^{x}$ eu caímos no próprio $e^{x}$ .

$\int e^{x} d x = e^{x} + C$

Calma jovem gafanhoto, a questão não acabou ainda, nos foi dada a informação de que o valor da primitiva ( $F (x)$ ) para $x = 0$ é igual à $3$ , com essa informação podemos achar o valor de $C$ .

$F (x) = e^{x} + C$

$F (0) = e^{0} + C$

$3 = 1 + C$

$C = 3 - 1$

$C = 2$

Assim, descobrimos que a função primitiva que gerou a função que está no integrando, para esse caso, é $F (x) = e^{x} + 2$ .

Tabela de integrais

Assim como nas derivadas, após os matemáticos realizarem o cálculo das primitivas de várias funções, foi montada uma tabela de integrais, para facilitar o cálculo delas, abaixo temos algumas funções e suas integrais:

Função	Integral
$f (x) = x^{n}, n \neq 1$	$F^{'} (x) = \frac{x^{n + 1}}{n + 1} + C$
$f (x) = k$	$F^{'} (x) = k x + C$
$f (x) = sen (x)$	$F^{'} (x) = - \cos (x) + C$
$f (x) = \cos (x)$	$F^{'} (x) = sen (x) + C$
$f (x) = \sec^{2} (x)$	$F^{'} (x) = \tan (x) + C$
$f (x) = \frac{1}{x} = x^{- 1}$	$F^{'} (x) = \ln \| x \| + C$
$f (x) = e^{x}$	$F^{'} (x) = e^{x} + C$

Como deve ter percebido, a tabela de integrais é praticamente o contrário da tabela de derivadas, muitos alunos acabam confundindo uma com a outra, mas com uma grande quantidade de exercícios resolvidos, é possível diminuir e até extinguir essa troca entre uma e outra. Essas não são todas as integrais possíveis, mas são o mínimo que devemos saber para resolver questões.

Definição intuitiva de integral

Se você teve física no ensino médio, talvez seu professor tenha falado que no movimento uniformemente variado (onde a aceleração é constante, fazendo com que a velocidade aumente sempre da mesma forma), a área embaixo do gráfico da velocidade pelo tempo é numericamente igual a distância percorrida. Tomando um gráfico de velocidade por tempo qualquer como exemplo:

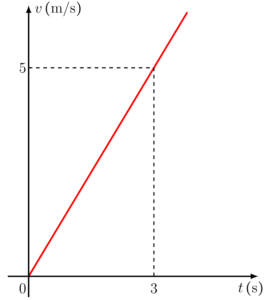
A área da figura formada entre o gráfico e o eixo do tempo, será igual, em módulo, a distância percorrida do objeto, pessoa ou veículo.

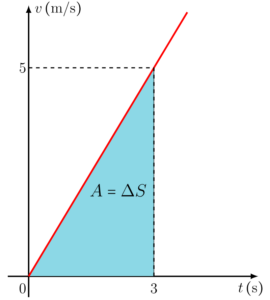
A figura acima é uma velha conhecida nossa, um triângulo, e para calcular a área dele basta multiplicar o comprimento da base pela altura e dividir por $2$ . No gráfico acima teremos a seguinte área:

$A = \frac{b \times h}{2} = \frac{3 \times 5}{2} = \frac{15}{2} = 7, 5 metros$

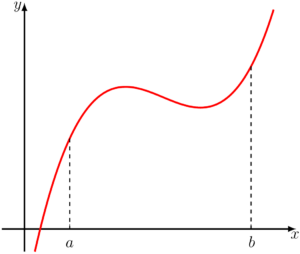
Quando a figura em baixo do gráfico é um polígono conhecido, como um quadrado, trapézio ou triângulo, fica fácil achar sua área, mas e se precisássemos calcular a área embaixo de desse gráfico em um intervalo de $a$ até $b$ (sendo $a$ e $b$ valores quaisquer, onde $a < b$ ):

Essa figura é cheia de curvas, que não são arredondadas como uma circunferência, tornando difícil ou até impossível identificar que equação utilizar para calcular sua área. E foi para resolver esse problema que um matemático chamado Bernhard Riemann propôs a seguinte interpretação:”Se utilizarmos uma figura geométrica que conhecemos, como o retângulo, para dividir a área da figura abaixo do gráfico, a soma das áreas dessas figuras dariam um valor próximo ao da área embaixo do gráfico” (não foi exatamente isso que ele disse, mas cabe aqui uma adaptação para melhor compreensão). Em outras palavras, ao invés de olharmos para essa figura como um único polígono, podemos imaginar que a área é a soma de vários retângulos um do lado do outro.

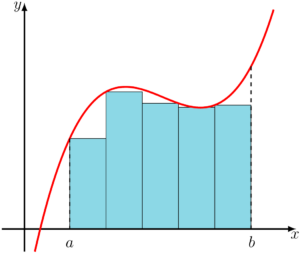
Como muitos de vocês podem ter observado, há um espaço faltante entre os retângulos e a curva do gráfico, fazendo com que a área dos retângulos somados seja menor que a área embaixo do gráfico, mas e se aumentássemos a quantidade de retângulos diminuindo a base de cada um deles?

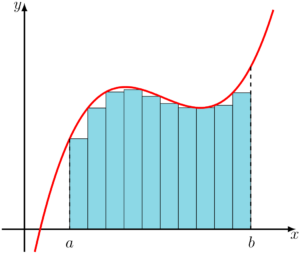
Na imagem acima temos o dobro de retângulos da imagem anterior, e se você prestar atenção, verá que aquelas espaços faltantes entre os retângulos e a curva, diminuíram, o que nos leva a concluir que o valor da soma das áreas dos retângulos será mais próxima da área que queremos calcular. Se ao invés de $10$ retângulos, tivéssemos $100$ ?

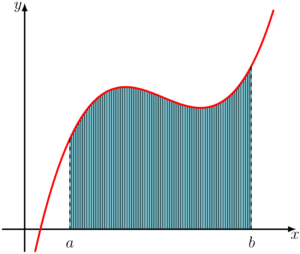
Visualmente, os espaços faltantes são quase imperceptíveis. Então, seguindo essa linha de raciocínio, se a base dos retângulos for tão pequena, mais tão pequena, ao ponto de nesse mesmo intervalo entre $a$ e $b$ , conseguirmos representar infinitos retângulos, a soma de todos os retângulos será praticamente igual a área embaixo do gráfico. E o cálculo dessa somatória de infinitas áreas, foi denominada “integral de Riemann”.

Assumindo que a altura desses retângulos são os valores da função $f (x)$ para diferentes valores de $x$ , que suas bases são um comprimento tão pequeno do eixo $x$ (chamamos esse pequeno intervalo de valores de $x$ , que tendem à zero, de $d x$ ), e que a área do retângulo é calculada pela multiplicação da base pela altura, podemos definir a integral como sendo uma somatória de infinitas multiplicações de $f (x)$ por $d x$ , partindo do ponto $a$ até um ponto $b$ .

$\int_{a}^{b} f (x) d x$

Nesse caso, o $\int$ pode ser entendido como o símbolo de uma somatória ( $Σ$ ), esticado infinitamente de forma que pareça um $S$ esticado, representando a soma de infinitos valores, e as letras $a$ e $b$ são os limites de integração, chamados limite inferior e superior, respectivamente (eles indicam qual a região do gráfico que quero calcular a área, ou para qual intervalo de valores de $x$ a função está definida).

Portanto, além da integral ser considerada uma antiderivada, ela pode ser interpretada como a somatória de infinitas áreas, que por sua vez, podem representar a área embaixo do gráfico de uma função. Vale ressaltar que essas não são as únicas interpretações para a integral e que há uma definição estrita que deixei de comentar, pois o aprofundamento desse assunto requer um estudo que não caberia nesse artigo, a nível de ensino superior, as noções de integral aqui mencionadas são suficientes.

Como calcular uma integral definida?

Para calcularmos uma integral definida, utilizaremos a segunda parte do Teorema fundamental do cálculo, ela diz que a integral de uma função $f (x)$ qualquer, definida para um intervalo de valores de $x$ compreendido entre $a$ e $b$ , vai ser igual à primitiva de $f (x)$ calculada para $x = b$ menos a primitiva para $x = a$ .

$\int_{a}^{b} f (x) d x = F (b) - F (a)$

Se você não entendeu muita coisa do que eu disse, irei tentar explicar de outra forma. Basicamente, a integral de uma função para um intervalo qualquer (de $x = 1$ até $x = 3$ , por exemplo), vai ser igual a calcularmos a integral indefinida (primitiva) da função, substituir o valor do limite superior ( $b$ ) onde tiver $x$ na primitiva e subtrair do valor da primitiva depois de substituir o limite inferior ( $a$ ). Vamos resolver uma questão para facilitar o entendimento.

Exemplo 1: Calcule a integral definida abaixo.

$\int_{0}^{1} x^{2} d x$

Primeiramente, calculamos a integral indefinida da função $x^{2}$ , ou seja, qual função que ao derivarmos, caímos em $x^{2}$ . Utilizando a tabela de integrais a nosso favor, quando temos $x$ elevado a um expoente que seja diferente de $- 1$ , a integral disso vai ser $x$ elevado ao expoente antigo mais um, dividido pelo novo expoente:

$\int x^{2} d x = \frac{x^{2 + 1}}{2 + 1} + C = \frac{x^{3}}{3} + C$

Em seguida, calculamos o valor da função primitiva ( $\frac{x^{3}}{3} + C$ ) para $x = 1$ (limite superior).

$F (b) = F (1) = \frac{1^{3}}{3} + C = \frac{1}{3} + C$

Então, calculamos o valor da primitiva para $x = 0$ .

$F (b) = F (0) = \frac{0^{3}}{3} + C = 0 + C = C$

Por fim, substituímos na equação do TFC (Teorema Fundamental do Cálculo):

$\int_{a}^{b} f (x) d x = F (b) - F (a)$

$\int_{0}^{1} x^{2} d x = F (1) - F (0)$

$\int_{0}^{1} x^{2} d x = \frac{1}{3} + C - C$

$\int_{0}^{1} x^{2} d x = \frac{1}{3}$

Percebeu que as constantes $C$ se anularam? Isso sempre acontecerá quando você calcular a integral definida, digamos que isso é um “efeito colateral da aplicação do TFC”, portanto, quando a integral for definida, não precisa escrever o $C$ nos cálculos.

Exemplo 2: Resolva a integral abaixo.

$\int_{1}^{3} 2 d x$

Temos aqui uma função constante, e de acordo com a tabela, a integral de uma constante é igual à constante vezes a variável independente, nesse caso a integral será $2 x$ . Achada a primitiva, calculamos a integral definida:

$\int_{1}^{3} 2 d x = 2 \times 3 - 2 \times 1 = 6 - 2 = 4$

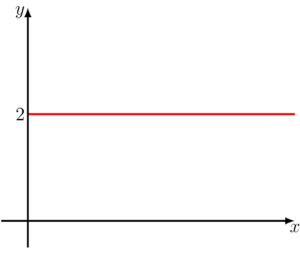
Supondo que esse valor encontrado fosse a área embaixo do gráfico da função $f (x) = 2$ , como poderíamos interpretar esse cálculo geometricamente? Antes de tudo, precisamos saber qual é o gráfico da função $f (x) = 2$ :

A área que queremos calcular é a que está entre os valores de $x = 1$ e $x = 3$ .

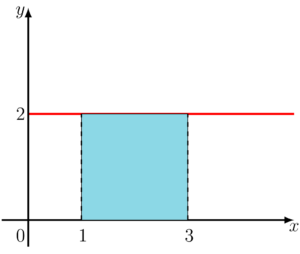
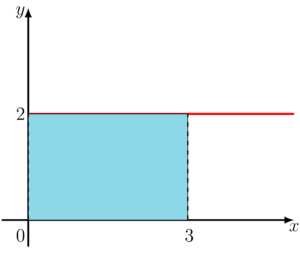
Ao calcularmos $F (3)$ , estamos encontrando a área que começa no eixo $f (x)$ e vai até $x = 3$ .

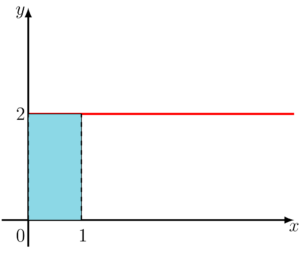
Já quando achamos $F (1)$ , encontramos a pequena área compreendida entre o eixo $f (x)$ e $x = 1$ .

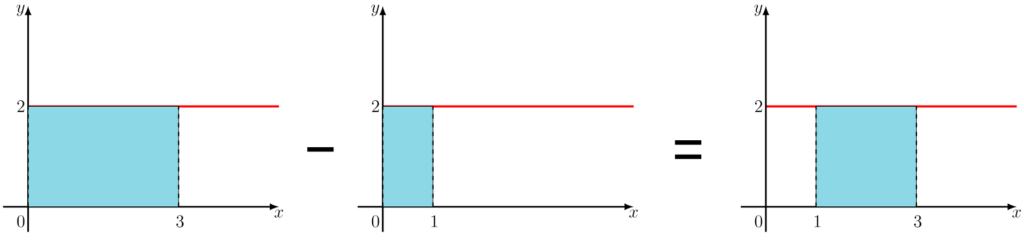
Então, quando calculamos $F (3) - F (1)$ , subtraímos a área que não queremos $F (1)$ , da área total $F (3)$ , restando assim a área entre $x = 1$ e $x = 3$ .

É importante mencionar que essa interpretação geométrica é interessante e faz sentido para muitas funções, no entanto, ela não condiz exatamente com o significado estrito da integral, e foi utilizada por mim apenas para uma melhor visualização e entendimento do assunto. Por fim, mas não menos importante, haverá situações, que o resultado da integral definida será negativo, e você pode se perguntar:”Não existem áreas negativas, o que isso significa então?”, levando em conta que há funções que possuem o gráfico abaixo do eixo $x$ :

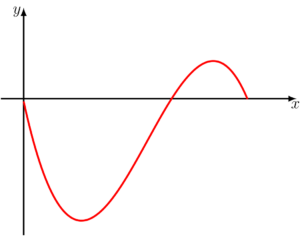
O sinal negativo pode indicar duas coisas, ou o gráfico está abaixo do eixo $x$ , ou a parte do gráfico que está abaixo do eixo $x$ é maior que a que está acima dele, portanto, se o exercício pedir a área, basta tirar o módulo do valor negativo.

Propriedades das integrais

Existem determinadas relações que facilitam o cálculo e a manipulação das integrais, essas são as propriedades. Podemos dividi-las em propriedades das integrais indefinidas e definidas.

Propriedades das integrais indefinidas:

Quando tivermos uma constante multiplicando uma função, podemos “puxá-la” para fora da integral, fazendo com que consigamos calcular a integral normalmente e depois multiplicarmos o resultado pela constante, diminuindo o tamanho dos valores nos cálculos.

$\int k \times f (x) d x = k \int f (x) d x$

Exemplo: Calcule a integral abaixo

$\int 5 s e n (x) d x$

Na integral acima, temos a função $s e n (x)$ sendo multiplicada pela constante $5$ , de acordo com a propriedade que acabamos de ver, é possível puxar o $5$ para fora da integral:

$\int 5 s e n (x) d x =$ 5\int sen(x)\;dx$$

Agora é só calcular a integral primitiva de $s e n (x)$ e multiplicar pela constante $5$ .

$5 \int s e n (x) d x = 5 \times c o s (x) + C = 5 c o s (x) + C$

A segunda e a terceira propriedades são muito parecidas, quando tivermos integrando uma soma de funções, podemos calcular a integral de cada função separadamente e somar os resultados, em outras palavras, “a integral da soma é igual à soma das integrais”.

$\int f (x) + g (x) d x = \int f (x) d x + \int g (x) d x$

Podemos fazer o mesmo para funções que estão sendo subtraídas.

$\int f (x) - g (x) d x = \int f (x) d x - \int g (x) d x$

Exemplo: Calcule a integral abaixo

$\int e^{x} + 2 x d x$

Podemos separar essa integral em duas, uma para a função $e^{x}$ e outra para a função $2 x$ .

$\int e^{x} + 2 x d x = \int e^{x} d x + \int 2 x d x$

Restou apenas calcular as integrais.

$\int e^{x} + 2 x d x = \int e^{x} d x + \int 2 x d x = e^{x} + x^{2} + C$

Se você se perguntou:”Não seria 2C, já que são duas funções?”, parabéns, pois esse é um detalhe que passa despercebido por muitos alunos. O motivo pelo qual escrevemos apenas $C$ , é que uma constante mais (ou menos) outra constante, continua sendo uma constante, exemplo: $2 + 3 = 5$ , o $2$ é constante, o $3$ é constante e a soma disso também é uma constante ( $5$ ), então podemos escrever apenas $C$ , que vai englobar todas as constantes das funções.

Propriedades das integrais definidas:

Se os limites de integração forem iguais, o resultado da integral definida será igual à zero, pois é como se você estivesse calculando uma área menos ela mesmo, e o resultado disso será zero.

$\int_{a}^{a} f (x) d x = 0$

Caso os limites de integração estejam em uma ordem tal que lhe cause dificuldade ao substituir na equação do TFC, podes inverter o limite superior com o inferior, mas para que você não altere a integral, será necessário multiplicar ela por $- 1$ .

$\int_{a}^{b} f (x) d x = - \int_{b}^{a} f (x) d x$

Por mais que pareça que você nunca irá inverter os limites, em algumas aplicações de integrais sua vida será facilitada ao invertê-los.

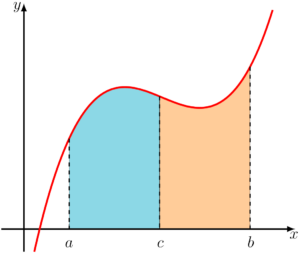
Uma vez que a integral está sendo calculada para um intervalo entre $a$ e $b$ , é possível separar isso na integral de $a$ até um ponto $c$ (que está entre $a$ e $b$ ) mais a integral de $c$ até $b$ .

$\int_{a}^{b} f (x) d x = \int_{a}^{c} f (x) d x + \int_{c}^{b} f (x) d x$

Esse processo é o equivalente a você dividir uma área em duas e depois somá-las, o resultado será o mesmo que calcular a área total, mas a depender da situação, esse artifício será necessário.

Não posso deixar de mencionar que as propriedades das integrais indefinidas funcionam para as definidas, uma vez que antes de substituir os limites de integração, calculamos uma integral indefinida.

Métodos de integração

Como nem tudo são flores, conhecer a tabela de integrais não será suficiente para calcular a integral para toda e qualquer tipo de função, e para cada situação, existe um método de integração específico. Para a tristeza de alguns e alegria de outros, diferentemente das derivadas, não são apenas três métodos, e cada um merecendo um artigo próprio para um melhor entendimento.

Integrais por substituição:

Quando o integrando é uma função composta ou temos uma multiplicação entre funções, onde uma delas é derivada da outra, precisaremos realizar uma substituição de uma das funções por uma letra, a fim de simplificar a integral e podermos utilizar a tabela para calcular.

Exemplos de integrais por substituição:

1) $\int s e n (2 x + 1) d x$

2) $\int e^{3 x} d x$

3) $\int s e n (\frac{1}{x}) l n | x | d x$

Integrais por partes:

Caso a função composta ou o produto entre funções no integrando não puder ser simplificada através do método da substituição, utilizamos a integração por partes, onde utilizamos a seguinte equação para resolver:

$\int f (x) \times g (x) d x = \int u d v = u \times v - \int v d u$

O “ $u$ ” será uma função dentre $f (x)$ e $g (x)$ que será derivada e “ $d v$ ” será a função a ser integrada, de acordo com a equação acima.

Exemplos de integrais por partes:

1) $\int e^{x^{2}} d x$

2) $\int s e n (x) e^{x} d x$

3) $\int e^{x} 3 x^{3} d x$

Integrais trigonométricas:

Se o integrando for uma função trigonométrica elevada a algum expoente diferente de $1$ ou uma multiplicação delas, será necessário utilizar algumas relações trigonométricas e manipulações matemáticas para simplificar a integral.

Exemplos de integrais trigonométricas:

1) $\int s e n^{2} (x) d x$

2) $\int c o s^{5} (x) d x$

3) $\int s e n^{2} (3 x) c o s^{4} (3 x) d x$

Integrais por substituição trigonométrica:

Em situações em que determinados termos estão presentes no integrando, é possível transformar uma expressão polinomial em uma expressão trigonométrica, possibilitando a simplificação da integral por meio de manipulações matemáticas e identidades trigonométricas.

Exemplos de integrais por substituição trigonométrica:

1) $\int \sqrt{1 + x^{2}} d x$

2) $\int x^{2} \sqrt{x^{2} - 4} d x$

3) $\int \frac{1}{\sqrt{3 - 2 x^{2}}} d x$

Integrais por frações parciais:

Quando o integrando for uma função racional (uma função constituída por polinômios se dividindo), na maioria dos casos será necessário utilizar o método de decomposição em frações parciais para simplificar a função transformando ela em uma soma de frações mais simples.

Exemplos de integrais por frações parciais:

1) $\int \frac{x^{2} - 3 x + 2}{x^{2} + 4 x + 4} d x$

2) $\int \frac{x + 1}{x^{2} + 6 x + 5} d x$

3) $\int \frac{x^{3} - 8}{x^{2} + 1} d x$

Integrais impróprias:

Esse método se aplica apenas para integral definida, se ao menos um dos limites de integração for $\infty$ ou $- \infty$ , a integral será considerada imprópria e utilizaremos o assunto de limites para resolver.

Exemplos de integrais impróprias:

1) $\int_{- \infty}^{0} \frac{1}{x^{2} + 2 x + 1} d x$

2) $\int_{- \infty}^{\infty} e^{x} d x$

3) $\int_{0}^{\infty} \frac{1}{x^{2}} d x$

Aplicações de integrais

Além do cálculo da área abaixo de um gráfico, podemos calcular a área entre dois gráficos, o volume de um sólido de revolução, a seção transversal de um sólido e muito mais, fazendo da integral uma ferramenta poderosíssima e indispensável para quem estiver cursando ou pretenda cursar alguma faculdade de exatas.

Daniel Duarte

Formado em Eletrotécnica pelo IFRN, além de ter cursos de Matemática Básica e Cálculo pela empresa Help Engenharia.

Sobre nós

O Matematiquês é um blog dedicado ao aprendizado de matemática, e nosso objetivo é tornar o ensino mais acessível e envolvente através de conteúdos de alta qualidade e gratuitos para alunos e professores em todo o Brasil. Buscamos simplificar conceitos complexos com uma abordagem clara e direta, priorizando transparência, diversidade, clareza, qualidade, inovação e compromisso social. Nosso blog oferece conteúdos fundamentados por especialistas, revisados com rigor e atualizados.

Categorias

Posts mais recentes

All Post
Curiosidades
Ensino Fundamental
Ensino Médio
Ensino Superior
Notícias

Back
Cinemática
Dinâmica
Conceitos básicos da física

Back
Conceitos básicos da matemática
Frações
Potenciação
Radiciação
Geometria plana
Logaritmo

Back
Funções
Equações
Conjuntos numéricos
Geometria espacial
Inequações
Módulo
Progressões matemáticas
Física
Trigonometria
Cinemática
Dinâmica
Conceitos básicos da física

Back
Limites
Derivadas
Integrais
Equações Diferenciais
Vetores e Geometria Analítica

Integrais: O que é, como calcular e suas aplicações

O que é a integral?

Como calcular uma integral indefinida?

Tabela de integrais

Definição intuitiva de integral

Como calcular uma integral definida?

Propriedades das integrais

Propriedades das integrais indefinidas:

Propriedades das integrais definidas:

Métodos de integração

Integrais por substituição:

Integrais por partes:

Integrais trigonométricas:

Integrais por substituição trigonométrica:

Integrais por frações parciais:

Integrais impróprias:

Aplicações de integrais

Sobre nós

Categorias

Posts mais recentes

Aplicação de derivadas: Máximos e mínimos de uma função

Integral por Substituição: Como identificar e aplicar o método

Integrais: O que é, como calcular e suas aplicações

Tags

Matematiquês © 2024. Todos os direitos reservados.