Considerado por muitos como o terror do cálculo, esse é um assunto importantíssimo para quem cursa alguma faculdade de exatas, como engenharia, química ou física, pois além de ser uma das bases dessa matéria tão infame, ele acompanhará o aluno para além do cálculo, sendo utilizado em matérias como física, mecânica dos fluidos e resistência dos materiais. No entanto, dependendo da forma que ele é explicado, o assunto “derivadas” pode ser considerado o mais tranquilo dentre seus colegas limites e integrais.
O que é a derivada?
Derivadas, muitas vezes chamado de diferencial, é um assunto de uma matéria de ensino superior chamada cálculo, cujo significado é “estudo das funções”, ou seja, tudo relacionado ao cálculo gira em torno das funções, sendo indispensável entendê-las para não ter dificuldade nela.
Dada essa introdução, o significado de “derivada” é taxa de variação de uma função, em outras palavras, calcular a derivada de uma função é descobrir como seu valor varia de acordo com os valores que a variável independente assume.
Eu sei, parece confuso, mas vamos analisar um exemplo para facilitar o entendimento, observemos a função $f(x)=2x+1$, o que acontecerá com o valor de $f(x)$ se o $x$ for aumentando?
$$f(0)=2.0+1=1$$
$$f(1)=2.1+1=3$$
$$f(2)=2.2+1=5$$
$$f(3)=2.3+1=7$$
Percebe que, cada vez que eu aumento uma unidade no valor de $x$ (variável independente), $f(x)$ aumenta em duas unidades? Podemos dizer, com nossa breve observação, que a taxa de variação da função $f(x)=2x+1$ é $2$, no entanto, na matemática não podemos afirmar nada com base em observações de um caso isolado, para isso é que existe a derivada, que aprenderemos a calcular a seguir.
Derivada pela definição
Mostrarei nesse tópico como a derivada foi criada a partir dos limites, e todo o processo pode parecer complicado, extenso e confuso, mas não se preocupe, pois para derivarmos uma função, utilizaremos uma tabela que facilitará muito a nossa vida, como explicarei posteriormente. Para descobrir o quanto que algo varia em relação a um outro parâmetro que também está mudando, nós dividimos esses dois valores, por exemplo, na física, quando queremos calcular a velocidade média de um veículo que mantém a velocidade durante todo o percurso, utilizamos a famosa equação:
$$v_m=\frac{\Delta s}{\Delta t}=\frac{s-s_0}{t-t_0}$$
Pegamos a variação (representado pelo triângulo, chamado de delta) do espaço, ou seja, a distância que ele percorreu no trajeto analisado, e dividimos pelo intervalo de tempo decorrido desde o início até o final do percurso, ao fazermos isso teremos como resultado a taxa média de variação do espaço em relação ao tempo, de forma mais simples, descobriremos quantos quilômetros o carro percorreu a cada hora. Para calcular a taxa de variação de uma função faremos o mesmo, definiremos um intervalo de valores de $f(x)$ e dividiremos por um intervalo de valores de $x$.
Utilizemos nesse primeiro exemplo a função $f(x)=2x+1$, vamos calcular a taxa de variação média ($T_{vm}$), no intervalo de $f(1)$ até $f(3)$
$$f(x)=2x+1$$
$$T_{vm}f=\frac{f(3)-f(1)}{3-1}$$
$$T_{vm}f=\frac{7-3}{3-1}$$
$$T_{vm}f=\frac{4}{2}$$
$$T_{vm}f=2$$
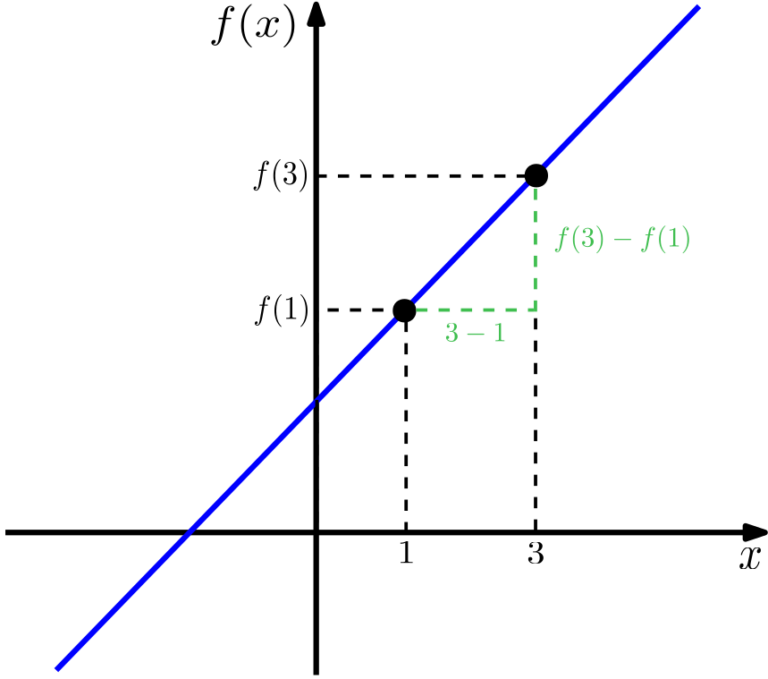
Como já tínhamos observado, a taxa de variação dessa função é $2$. A derivada também é chamada de “inclinação da função”, então o que calculamos acima foi a inclinação da função $f(x)=2x+1$, e ela vai ser a mesma independente de quais intervalos utilizemos para fazer o cálculo (podemos perceber isso pela reta sempre manter a mesma inclinação e nunca curvar), no entanto, a maioria das funções são mais complexas que ela, onde o gráfico delas não é uma simples reta, mas possuem curvas, e conforme o gráfico muda sua inclinação, a derivada irá mudar também.
Então era necessário que os matemáticos desenvolvessem uma equação geral que nos permitisse calcular a derivada independentemente da função estudada, e para isso, explicar como o fizeram, tomemos uma função qualquer cuja inclinação (derivada) varia:
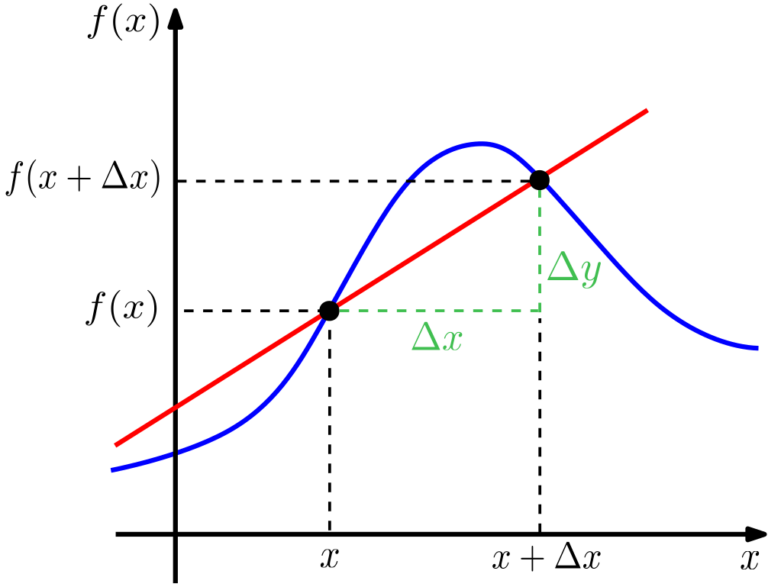
Essa reta vermelha no gráfico acima representa a inclinação da função para esse intervalo demarcado, entre $f(x+\Delta x)$ e $f(x)$, mas há algo estranho nisso, pois a inclinação do gráfico muda muito durante esse intervalo, tem partes em que a função está crescendo, e outras que ela está decrescendo, então, não está precisa essa reta, mas e se diminuíssemos o intervalo? O que aconteceria com a inclinação calculada?
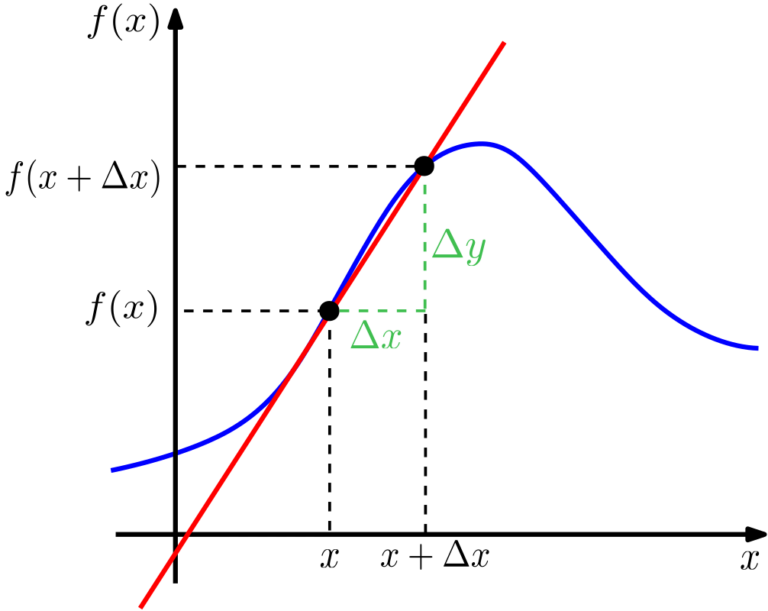
Como podemos observar, a inclinação da reta vermelha se aproximou da inclinação da própria função (representada pelo gráfico em azul) para esse intervalo menor, mas ainda há como melhorarmos isso, vamos aproximar os dois pontos de tal maneira que a distância entre eles ($\Delta x$) vai ser tão pequena, tão pequena, que tenderá a zero (mas não será zero):
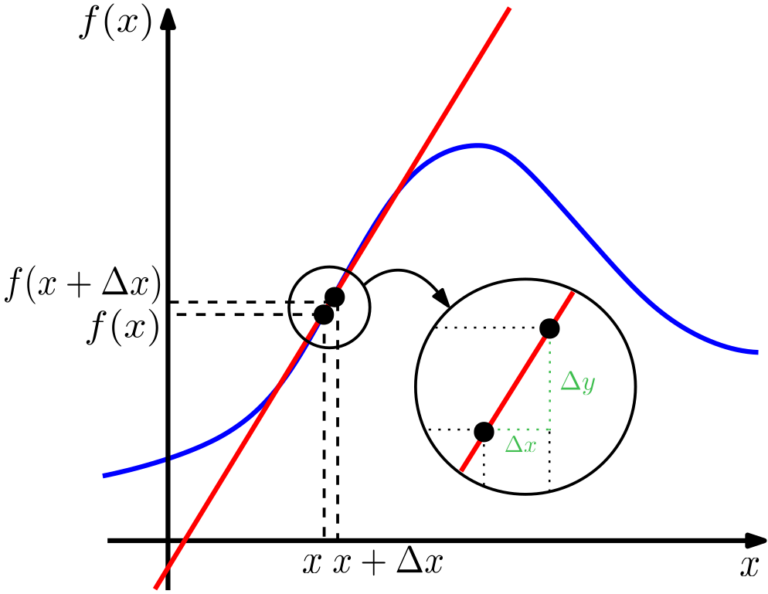
Na situação acima, temos um minúsculo intervalo de $f(x)$ sendo dividido por um minúsculo intervalo de $x$, e nesse caso, a reta que representa a derivada coincide praticamente de forma perfeita com a nossa função, traduzindo isso em uma equação matemática temos:
$$f’(x)=\frac{dy}{dx}=\displaystyle\lim_{\Delta x\to0}\frac{f(x+\Delta x)-f(x)}{\Delta x}$$
O $dy$ representa o intervalo infinitamente pequeno de valores de $f(x)$ e o $dx$ representa o mesmo só que para valores de $x$. Temos que nos atentar a um detalhe importante, essa equação nos permite calcular a derivada em um único ponto, ou seja, podemos calcular a derivada da função para $x=1$ ou para $x=2$, mas nunca para $x$ entre $1$ e $2$ ou entre qualquer outro intervalo.
A pergunta que não quer calar, como que calculamos a derivada utilizando essa equação? Pegaremos a função que queremos calcular a taxa de variação e substituiremos os valores correspondentes nela, e então resolvemos o limite. Mas antes disso, vale uma pequena revisão, se eu pedir para você calcular $f(2)$ na função $f(x)=x^2$, irás substituir o $2$ onde tiver $x$ na função:
$$f(2)=2^2=4$$
Mas e se ao invés de um número, eu te pedir para substituir uma letra? O processo será o mesmo, tomemos a mesma função, se eu quiser calcular $f(a)$, substituirei o $a$ onde tiver $x$ na função:
$$f(a)=a^2$$
Então, por lógica, para calcular $f(x+\Delta x)$, substituímos tudo isso onde tiver $x$:
$$f(x+\Delta x)=(x+\Delta x)^2=x^2+2x\Delta x+{\Delta x}^2$$
Fiz essa breve revisão para entendermos o processo de utilização da “equação da derivada pela definição”. Vamos calcular a taxa de variação daquela função $f(x)=2x+1$, só que dessa vez, calcularemos de forma matematicamente correta e precisa.
$$f’(x)=\displaystyle\lim_{\Delta x\to0}\frac{f(x+\Delta x)-f(x)}{\Delta x}$$
Já que $f(x)$ é a mesma coisa que $2x+1$, onde tiver $f(x)$ na equação acima, colocaremos $2x+1$:
$$f’(x)=\displaystyle\lim_{\Delta x\to0}\frac{2(x+\Delta x)+1-(2x+1)}{\Delta x}$$
Agora iremos manipular as expressões para eliminarmos o $\Delta x$, porque uma vez que a gente substitua $0$ onde tiver $\Delta x$, para resolver o limite, chegaremos em um problema:
$$f’(x)=\displaystyle\lim_{\Delta x\to0}\frac{2(x+0)+1-(2x+1)}{0}$$
$$f’(x)=\displaystyle\lim_{\Delta x\to0}\frac{2x+1-2x-1}{0}$$
$$f’(x)=\displaystyle\lim_{\Delta x\to0}\frac{0}{0}$$
Temos uma indeterminação, e se pudéssemos eliminar esse $zero$ que está no denominador, a indeterminação não aconteceria, e quem que substituímos para pôr o zero? O $\Delta x$, é por isso que precisamos eliminá-lo de alguma forma para podermos resolver o limite e assim calcularmos a derivada da função
$$f’(x)=\displaystyle\lim_{\Delta x\to0}\frac{2(x+\Delta x)+1-(2x+1)}{\Delta x}$$
$$f’(x)=\displaystyle\lim_{\Delta x\to0}\frac{2x+2\Delta x+1-2x-1}{\Delta x}$$
$$f’(x)=\displaystyle\lim_{\Delta x\to0}\frac{2\Delta x}{\Delta x}$$
$$f’(x)=\displaystyle\lim_{\Delta x\to0}2$$
$$f’(x)=2$$
Olha só, chegamos no valor $2$, isso significa que a derivada, taxa de variação ou se preferir, inclinação da função $f(x)=2x+1$ é $2$.
Vale a pena ressaltar que a taxa de variação média não é a mesma coisa que a derivada, pois por definição, a derivada é a taxa de variação de uma função em um intervalo infinitamente pequeno, sendo necessário utilizar o limite para representar isso, já a $T_{vm}$ é uma média que calculamos a analisar um intervalo grande de valores, só utilizei ela para ajudar na explicação da origem da derivada, pois o processo é parecido.
Tabela de derivadas
Nesse momento deves estar pensando: “Socorro, calcular a derivada de uma função é trabalhoso e difícil demais!”, mas não se desespere, pois os matemáticos já calcularam inúmeras vezes a derivada de várias funções utilizando a equação que mostrei anteriormente, e ao fazerem isso, perceberam que há um certo padrão, sendo criada uma tabela que indica a derivada das funções mais comuns:
Função:
$$f(x)=x^n$$
Derivada:
$$f’(x)=n.x^{n-1}$$
Função:
$$f(x)=k$$
Derivada:
$$f’(x)=0$$
Função:
$$f(x)=sen(x)$$
Derivada:
$$f’(x)=cos(x)$$
Função:
$$f(x)=cos(x)$$
Derivada:
$$f’(x)=-sen(x)$$
Função:
$$f(x)=tan(x)$$
Derivada:
$$f’(x)=sec^2(x)$$
Função:
$$f(x)=ln(x)$$
Derivada:
$$f’(x)=\frac{1}{x}$$
Função:
$$f(x)=e^x$$
Derivada:
$$f’(x)=e^x$$
Tens que ter gravadas no sangue as derivadas acima, e por mais que pareça complicado decorar essa tabela, quanto mais você fizer exercícios de derivadas, naturalmente as saberá sem precisar ficar revisitando a tabela. Vou só explicar as duas primeiras derivadas que podem parecer confusas, quando temos uma função que possui uma variável elevada a um número qualquer, para derivá-la, tombamos esse expoente, e então ele passará a multiplicar a letra, e subtraímos uma unidade do expoente antigo.
Exemplo:
Derive a função $f(x)=x^3$
Temos uma função que tem uma variável ($x$ nesse caso) elevada a um expoente numérico, para derivar ela, não precisamos passar por todo aquele processo trabalhoso ao utilizarmos aquela equação que tem limite no meio, basta tombarmos o expoente $3$ e subtrair uma unidade do expoente antigo
$$f(x)=x^3$$
$$f’(x)=3x^{3-1}$$
$$f’(x)=3x^2$$
Está derivada a função, simples e prático. Agora sobre a função $f(x)=k$, esse $k$ é uma constante qualquer, ou seja, um número, a derivada de uma constante, de acordo com a tabela, é igual à zero, então se derivarmos a função $f(x)=10$, o resultado será $f’(x)=0$ e isso irá funcionar para qualquer função constante.
Propriedades das derivadas
Como quase tudo na vida, há sempre algo mais a se aprender, há duas propriedades que tornarão o processo bem mais tranquilo.
Derivada de uma soma:
Quando temos uma função composta, que possui mais de um termo (função) sendo somados ou subtraídos, podemos derivar cada um deles individualmente, em outras palavras, a derivada de uma soma é igual à soma das derivadas.
Exemplo:
Derive a função $f(x)=x^2+5+sen(x)$
A função acima possui três termos se somando, então podemos derivar cada um individualmente, vamos colocar o apóstrofo nos termos para indicar que iremos derivá-los
$$f’(x)=(x^2)’+5’+(sen(x))’$$
Para derivar $x^2$, tombamos o expoente $2$ e subtraímos $1$ do expoente antigo (que é o próprio $2$), em relação ao $5$, sua derivada é zero, pois é uma constante, e a derivada de $sen(x)$ é $cos(x)$, portanto, a derivada da função $f(x)$ é:
$$f’(x)=2x^1+0+cos(x)$$
$$f’(x)=2x+cos(x)$$
Constantes multiplicando ou dividindo na derivada:
Se tivermos uma constante multiplicando ou dividindo um termo que possua a variável pela qual estamos derivando, não fazemos nada com ela, ou seja, ela vai continuar multiplicando ou dividindo a função, mesmo depois de derivarmos.
Exemplo:
Derive a função $f(x)=4ln|x|$
Temos o $4$, que é uma constante, multiplicando a função $ln|x|$, portanto, ao derivarmos o log, não mexeremos na constante
$$f(x)=4ln|x|$$
$$f’(x)=4\cdot\frac{1}{x}$$
$$f’(x)=\frac{4}{x}$$
Com esses conhecimentos, podemos derivar a nossa velha conhecida função $f(x)=2x+1$ utilizando a tabela e as propriedades (lembrando que o resultado deve ser $2$, independentemente do método que calculemos a derivada). O expoente do $x$ é $1$, mas o processo será o mesmo, tombaremos o $1$, então ele multiplicará tanto o $2$, quanto o $x$ e subtrairemos $1$ do expoente antigo
$$f(x)=2x+1$$
$$f’(x)=1.2x^{1-1}+0$$
$$f’(x)=2x^0$$
$$f’(x)=2.1$$
$$f’(x)=2$$
Bem mais rápido e sem complicação alguma.
Derivada em um ponto qualquer
Há funções como as de primeiro grau, cuja derivada vai ser a mesma independentemente do ponto que for analisado, como vimos no caso da função $f(x)=2x+1$, onde a derivada é sempre $2$, mas para muitas funções a taxa de variação mudará a depender do ponto analisado, e para calcularmos a derivada em um ponto específico é muito simples, primeiramente, calculamos a derivada, e depois substituímos o valor da variável independente onde ela estiver na expressão.
Exemplo:
Calcule a inclinação da função $f(x)=4x^2$ para $x=5$
Como inclinação da função e derivadas são dois nomes diferentes para uma mesma coisa, o que a questão está pedindo é que derivemos a função, e para isso tombaremos o expoente e subtrairemos uma unidade do antigo expoente, e o $4$ que está multiplicando não será mexido
$$f(x)=4x^2$$
$$f’(x)=4.2x^1$$
$$f’(x)=8x$$
Agora, substituímos o valor de $x$ na expressão resultante e encontraremos a derivada para $x=5$
$$f’(x)=8x$$
$$f’(5)=8.5$$
$$f’(5)=40$$
Regras de derivação
Além da tabela, precisamos saber das três regras de derivação, que são essenciais para derivar corretamente alguns tipos de funções, ao dominá-las você conseguirá derivar qualquer função.
Regra do produto:
Quando tivermos uma função composta onde duas funções distintas estão se multiplicando, como derivaríamos elas? Mostrarei o jeito errado e que muita gente acha ser o correto quando se depara com essa situação.
Exemplo:
Derive a função: $g(x)=x^2.sen(x)$
Intuitivamente, podemos ser induzidos a pensar que para derivar essa função, basta derivarmos o $x^2$ e o $sen(x)$:
$$g(x)=x^2.sen(x)$$
$$g’(x)=(x^2)’.(sen(x))’$$
$$g’(x)=2x.cos(x)$$
Só que essa derivada está errada, e eu poderia comprovar isso ao integrar a expressão $2x.cos(x)$, pois a integral é o inverso da derivada, ou seja, ao integrar uma função que foi derivada, eu desfaço a derivação e volto a ter a função original, e isso não iria acontecer nesse caso, mas para não deixar confusas as coisas, acredite que está errada a derivação (porque de fato está), a forma correta de se derivar funções que estão se multiplicando é derivando a primeira função, multiplicando isso pela segunda função e somando com a primeira função vezes a derivada da segunda.
$$g(x)=x^2.sen(x)$$
$$g’(x)=(x^2)’.sen(x)+x^2.(sen(x))’$$
$$g’(x)=2x.sen(x)+x^2.cos(x)$$
Agora derivamos corretamente, o que deves se atentar é quem você irá considerar como “primeira função” e quem será a segunda, pois isso deverá ser respeitado na hora de realizar a derivação. De forma geral, a derivada do produto de duas funções é:
$$f(x)=u(x).v(x)$$
$$f’(x)=u’(x).v(x)+u(x).v’(x)$$
Regra do quociente:
Muito parecida com a regra do produto, a regra do quociente serve para casos em que temos uma divisão onde pelo menos o denominador terá uma função que possui a variável independente. Derivamos da seguinte forma:
$$f(x)=\frac{u(x)}{v(x)}$$
$$f’(x)=\frac{u’(x).v(x)-u(x).v’(x)}{v^2(x)}$$
Ou seja, derivamos a primeira função e multiplicamos isso pela segunda função, menos a primeira função vezes a derivada da segunda, por fim, dividimos tudo isso pela segunda função ao quadrado. Geralmente escolhemos a função do numerador para ser a “primeira”, e que está no denominador será a “segunda”.
Exemplo:
Derive a função $h(y)=\frac{y^3}{e^y}$
Temos uma divisão de duas funções que possuem a variável independente, que nesse caso é $y$, mas isso não irá mudar em nada o processo de derivação. Nossa primeira função será $y^3$ e a segunda $e^y$
$$h(y)=\frac{y^3}{e^y}$$
$$h’(y)=\frac{(y^3)’.e^y-y^3.(e^y)’}{(e^y)^2}$$
$$h’(y)=\frac{3y^2.e^y-y^3.e^y}{e^2y}$$
A função está derivada, mas há alguns professores que exigem que o aluno simplifique a expressão, então farei a simplificação para sanar a dúvida de quem tiver, colocarei o $e^y$ em evidência
$$h’(y)=\frac{3y^2.e^y-y^3.e^y}{e^2y}$$
$$h’(y)=\frac{e^y(3y^2-y^3)}{e^y.e^y}$$
$$h’(y)=\frac{3y^2-y^3}{e^y}$$
Regra da cadeia:
Deixei de fora uma informação crucial de propósito, só podemos derivar utilizando a tabela, caso a função seja exatamente igual à alguma da tabela, caso haja algo diferente do que temos na tabela, precisaremos usar a regra da cadeia para derivar, e para explicá-la, utilizarei um exemplo. Quase esqueci de falar, para entender essa regra, utilizarei a seguinte notação para a derivada:
$$\frac{dy}{dx}$$
Que significa a derivada da função $y$ em relação à variável independente $x$, e você entenderá o porquê em breve.
Exemplo:
Derive a função $y=sen(3x+2)$
Se procurarmos na tabela, encontraremos a função $y=sen(x)$, mas não é a que questão nos pede para derivar, o que faremos? Iremos substituir a expressão que diverge da tabela, pois se tivéssemos uma variável sozinha ali no argumento do seno, poderíamos derivar pela tabela, mas temos mais que isso. Vamos chamar todo o $3x+2$ de $u$
$$y=sen(3x+2)$$
$$y=sen(u)$$
Agora derivamos a função $y=sen(u)$ em relação à $u$ e derivamos $u=3x+2$ em relação à $x$
1)
$$y=sen(u)$$
$$\frac{dy}{du}=(sen(u))’$$
$$\frac{dy}{du}=cos(u)$$
2)
$$u=x+2$$
$$\frac{du}{dx}=(3x)’+2’$$
$$\frac{du}{dx}=3+0$$
$$\frac{du}{dx}=3$$
Paremos um pouco para pensar, tínhamos no começo a função $y=sen(3x+2)$ e queríamos derivá-la em relação à variável $x$, portanto, queríamos encontrar $y’$ ou $\frac{dy}{dx}$ (ambas as representações possuem o mesmo significado), mas de forma direta não conseguiríamos calcular, pois a função não está na tabela, então fizemos todo esse processo para chegarmos nisso indiretamente, pois concorda que se multiplicássemos $\frac{dy}{du}$ por $\frac{du}{dx}$, poderíamos simplificar o $du$, sobrando apenas $\frac{dy}{dx}$? É exatamente isso que faremos, multiplicaremos as duas derivadas e obteremos ao fazermos isso, a derivada da função $y=sen(3x+2)
$$\frac{dy}{du}\cdot\frac{du}{dx}=\frac{dy}{dx}=cos(u).3$$
Substituindo $u$ por $3x+2$, teremos:
$$\frac{dy}{dx}=3cos(3x+2)$$
No começo é confuso, mas conforme fores resolvendo exercícios, verás que é mais simples do que parece. Para facilitar sua vida, irei dar uma dica, quando tiveres uma função que não pertence à tabela, derive ela como se estivesse e multiplique pela derivada da expressão que diverge da tabela.
Exemplo:
Derive a função $f(x)=ln|x^2|$
Se tivéssemos apenas $x$ no logaritmando do log, bastaríamos derivar normalmente, mas como temos $x^2$, precisamos utilizar a regra da cadeia, e utilizando a dica que dei, podemos derivar o ln normalmente e multiplicarmos pela derivada de $x^2$
$$f(x)=ln|x^2|$$
$$f’(x)=\frac{1}{x^2}\cdot2x$$
$$f’(x)=\frac{2x}{x^2}$$
$$f’(x)=\frac{2}{x}$$
Aplicações de derivadas
Utilizamos as derivadas em vários assuntos para calcular determinados valores, e irei citar três aplicações muito interessantes.
Resolução de limites por derivadas (L’Hôpital):
Caso tenhamos um limite indeterminado do tipo $\frac{0}{0}$ ou infinito sobre infinito, podemos derivar numerador e denominador do limite, até eliminar a indeterminação, e assim resolver o limite. O nome dessa regra é L’Hôpital.
Máximos e mínimos:
Conseguimos descobrir qual é o valor máximo ou mínimo de uma função, e o ponto de inflexão, que é quando a concavidade se altera de cima para baixo ou vice-versa.
Otimização:
Podemos resolver problemas que envolvem situações em que precisamos alcançar um valor máximo de algo com o mínimo de recurso possível, como quantas latas de tinta precisamos para preencher determinada área gastando o menor valor. Esses tipos de exercícios são chamados “problemas de otimização”.
Notações de derivadas
Existem diferentes tipos de representações ou notações, para as derivadas, cada uma foi criada por um matemático diferente, sendo melhor utilizar uma ou outra a depender das situações, no entanto, todas possuem o mesmo significado.
Notação de Lagrange:
$$f’(x)=y’$$
Notação de Newton:
$$\dot{f}(x)=\dot{y}(x)$$
Notação de Leibniz:
$$\frac{df}{dx}=\frac{dy}{dx}$$
Notação de Arbogast:
$$D_{x}f=D_{x}y$$
As mais utilizadas são a de Lagrange e de Leibniz.
Derivada implícita
Por fim, mas não menos importante, vale a menção da derivação implícita, que é um método específico utilizado para derivar funções que estão na forma implícita (quando o $y$ não está isolado na expressão da função).
Exemplo:
Derive a função:
$$y^2-e^x=8$$
A função acima está na forma implícita, pois o $y$ não está isolado, então podemos usar a derivação implícita. Derivamos todos os termos da expressão, só que ao derivarmos o $y^2$, acrescentamos um $y’$ multiplicando.
$$y^2-e^x=8$$
$$2yy’-e^x=0$$
E então isolamos o $y’$
$$2yy’=e^x$$
$$y’=\frac{e^x}{2y}$$
Para saber mais sobre esse método, recomendo que leia o artigo que temos aqui no blog.
Exercícios resolvidos de derivadas
1. Derive a função $f(x)=4e^x+cos(x)$
Como a derivada de uma soma é igual à soma das derivadas, derivaremos cada termo individualmente
$$f(x)=4e^x+cos(x)$$
$$f’(x)=(4e^x)’-(sen(x))’$$
$$f’(x)=4e^x-sen(x)$$
2. Calcule a taxa de variação da função $g(u)=u^3.ln|u|$
Apesar de termos a letra $u$ como variável independente, tudo que aprendemos até o momento sobre derivadas se aplica da mesma forma. Há um produto (multiplicação) entre as duas funções, portanto, utilizaremos a regra do produto para derivar
$$g(u)=u^3.ln|u|$$
$$g’(u)=(u^3)’.ln|u|+u^3.(ln|u|)’$$
$$g’(u)=3u^2.ln|u|+u^3\cdot\frac{1}{u}$$
$$g’(u)=3u^2.ln|u|+\frac{u^3}{u}$$
$$g’(u)=3u^2.ln|u|+u^2$$
$$g’(u)=u^2(3ln|u|+1)$$
3. Qual é a inclinação da função abaixo?
$$y=\frac{1}{e^x-sen(x)}$$
Temos uma divisão com uma função que possui a variável independente no denominador, então devemos utilizar a regra do quociente, só que pode surgir uma dúvida, qual serão nossas primeira e segunda funções? A primeira será a função constante $1$ e a segunda será toda a função composta $e^x-sen(x)$
$$y=\frac{1}{e^x-sen(x)}$$
$$\frac{dy}{dx}=\frac{1’.(e^x-sen(x))-1.(e^x-sen(x))’}{(e^x-sen(x))^2}$$
$$\frac{dy}{dx}=\frac{0.(e^x-sen(x))-1(e^x-cos(x))}{(e^x-sen(x))^2}$$
$$\frac{dy}{dx}=\frac{0-e^x+cos(x))}{(e^x-sen(x))^2}$$
$$\frac{dy}{dx}=\frac{-e^x+cos(x))}{(e^x-sen(x))^2}$$
4. Determine f’(0) da função $f(x)=e^{x^2}$
Não temos a função acima na tabela, mas não estamos em um beco sem saída, podemos utilizar a regra da cadeia para derivar. Derivamos a função $e^{x^2}$ como se ela fosse $e^x$ e multiplicamos pela derivada de $x^2$:
$$f(x)=e^{x^2}$$
$$\dot{f}(x)=e^{x^2}.2x$$
$$\dot{f}(x)=2xe^{x^2}$$
