Esboçar o gráfico de uma função de 1° grau, 2° grau, trigonométrica ou exponencial é relativamente simples, mas como montar o gráfico de uma função complexa? Um dos artifícios que possibilitam essa façanha é a obtenção dos chamados “pontos críticos”, que nos ajudam a ter uma noção da aparência de certas funções mais elaboradas.
O que é o ponto de máximo ou mínimo de uma função?
São locais onde a função atinge seus valores mais altos (máximos) ou mais baixos (mínimos) dentro de um intervalo específico. Em termos práticos, um ponto de máximo é aquele em que a função apresenta o maior valor quando comparada a todos os pontos ao redor, enquanto um ponto de mínimo é onde a função apresenta o menor valor no mesmo contexto.
Visualmente, se considerarmos o gráfico de uma função, os pontos de máximo e mínimo se comportam como picos e vales. Esses pontos são crucialmente importantes em diversas áreas, como engenharia, economia e ciências naturais, onde é necessário otimizar algum parâmetro, como custo ou eficiência, em outras palavras, é necessário achar um valor máximo, gastando ou utilizando o mínimo de recursos.
Exemplo ilustrativo:
Imagine que você tem uma cerca de comprimento fixo e deseja cercar um terreno retangular. O objetivo é maximizar a área cercada. Você sabe que o comprimento da cerca será utilizado para formar os lados do retângulo, mas precisa decidir qual será a largura e o comprimento do terreno.
Neste caso, a área do terreno é dada pela multiplicação da largura pelo comprimento, e a cerca representa uma restrição, pois o perímetro do retângulo (a soma dos lados) deve ser igual ao comprimento fixo da cerca. O problema de otimização consiste em encontrar as dimensões do retângulo (largura e comprimento) que maximizam a área, dadas as restrições de perímetro.
O que acontece quando a derivada é igual à zero e quais as consequências?
A derivada de uma função em um determinado ponto fornece a inclinação da reta tangente à curva naquele ponto. Quando a derivada é igual a zero, isso significa que a inclinação da reta tangente é horizontal. Este fenômeno ocorre nos pontos locais de máximo, mínimo ou em pontos de inflexão (ponto onde a função muda de uma concavidade para outra).
Isso significa que ao calcularmos a derivada de uma função e a igualarmos a zero, acharemos os valores de
Como achar pontos de máximo e mínimo com derivada?
Encontrar pontos de máximo e mínimo de uma função utilizando derivadas envolve um processo metódico (que segue uma regra específica). Irei descrever as etapas a seguir.
Exemplo 1: Considere que a função
Primeiramente, calcularemos a derivada da função
O próximo passo é igualar a derivada a zero para encontrar os pontos críticos:
A partir disso, isolamos
Pelo contexto da questão, poderíamos parar aqui, pois esse valor encontrado já é o que a questão pede, mas suponhamos que não sabemos a sua natureza dele (se ele é um ponto de máximo, mínimo ou inflexão), para determinarmos isso precisamos fazer o “teste da segunda derivada”.
Esse teste consiste em derivamos a função uma segunda vez: Se a constante for positiva,
Como
Exemplo 2: Determine os pontos críticos da função abaixo.
Montei esse exercício para mostrar como proceder ao encontrar mais de um candidato a ponto crítico. Comecemos achando a derivada da função acima.
Agora igualamos a primeira derivada à zero para tentarmos achar os candidatos a pontos críticos.
Chegamos em uma equação quadrática, para resolvermos utilizaremos a “fórmula de Bháskara“.
Chegamos em dois valores, e para descobrirmos qual deles é o ponto de máximo ou mínimo, precisaremos derivar novamente a função.
Era exatamente nisso que queria chegar, ao invés de termos uma constante como resultado da segunda derivada, achamos uma expressão matemática, e agora, o que fazer? Substituiremos os candidatos a pontos críticos na segunda derivada, e de acordo com o sinal do resultado, determinaremos a natureza deles. Irei substituir primeiro o valor
Já que o resultado da segunda derivada para
Agora vamos analisar a segunda derivada para
Podemos determinar que
Deixando todas as frações com o mesmo denominador, teremos:
Vamos ver o gráfico da função para verificar se os valores obtidos estão corretos?
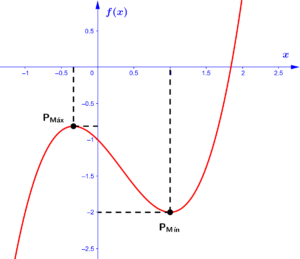
Um bônus para quem ficou até o fim do artigo, seria possível determinar o ponto de inflexão dessa função, ou seja, o ponto que define a mudança do ponto de máximo local para o ponto de mínimo local (mudança da concavidade). Para tal, igualaremos a segunda derivada à zero e isolaremos o
Fica como exercício encontrar o correspondente em





