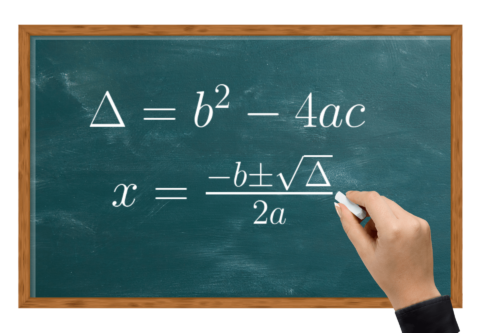Equação de 2º Grau: Guia Completo com Exemplos e Exercícios Resolvidos

Equações
ExercíciosTeoria
05/08/2024
Daniel Duarte

Fórmula de Bhaskara escrita em um quadro negro.

O que é equação de 2º grau?

É uma equação (expressão matemática que contém variáveis, números e uma igualdade), cuja principal característica é uma das incógnitas (ou variáveis) estar elevada ao quadrado. Sua forma geral é:

$a x^{2} + b x + c = 0$

Onde $a$ , $b$ e $c$ são números reais quaisquer e $a$ é diferente de zero. No entanto, assim como a equação de $1 °$ grau, ela nem sempre irá aparecer nessa forma nas questões, como veremos a seguir.

Equação de 2º grau completa

Uma equação de 2º grau completa é aquela que possui todos os termos: $a x^{2}$ , $b x$ e $c$ . Isso significa que os coeficientes $a$ , $b$ e $c$ são diferentes de zero. Por exemplo, a equação $2 x^{2} + 3 x + 1 = 0$ está na forma completa.

Exemplos:

1) $3 x^{2} + 5 x + 2 = 0$

2) $x^{2} - 4 x + 4 = 0$

3) $2 x^{2} + 7 x - 3 = 0$

Equação de 2º grau incompleta

Já a incompleta é aquela que não possui o termo $b x$ ou o termo $c$ , isso acontece quando os coeficientes desses termos são iguais a zero, caso o $a$ fosse igual à zero, a equação se tornaria de primeiro grau, então sempre consideramos ele diferente de zero, como já foi mencionado. Existem três tipos de formas incompleta da equação de $2 °$ grau:

Coeficiente C igual à zero:

$a x^{2} + b x = 0$

Coeficiente B igual à zero:

$a x^{2} + c = 0$

Coeficiente B e C iguais à zero:

$a x^{2} = 0$

Exemplos:

1) $2 x^{2} + 3 x = 0$

2) $x^{2} - 4 = 0$

3) $5 x^{2} = 0$

Como resolver uma equação de 2º grau completa?

Assim como a equação de 1º grau, precisamos isolar a variável, a fim de encontrar as soluções (ou raízes), só que na forma completa, é muito difícil isolá-la, no entanto, o matemático indiano Bhaskara Akaria, não somente descobriu como isolar a variável, mas criou uma fórmula que serve para resolver toda e qualquer equação de $2 °$ grau, contanto que saibamos os coeficientes $a$ , $b$ e $c$ . A ela foi dado o nome de fórmula de Bhaskara, em homenagem ao seu criador, e ela tem a seguinte forma:

$x = \frac{- b \pm \sqrt{∆}}{2 a}, ∆ = b^{2} - 4 a c$

Essa fórmula nos permite encontrar as raízes da equação, que são os valores de $x$ que tornam verdadeira a igualdade. E sim, você não leu errado, valores, pois dependendo do valor do delta ( $∆$ ), também chamado de discriminante, podemos ter uma, duas ou nenhuma raiz para a equação.

Delta maior que zero:

Se ∆>0, então há duas raízes

Delta igual a zero:

Se ∆=0, então há apenas uma raiz

Delta menor que zero:

Se ∆<0, então não há nenhuma raiz, no conjunto dos números reais

Para que não tenhas dificuldade em encontrar os coeficientes, independentemente do jeito que a expressão matemática for dada nas questões, saiba que o $a$ será sempre quem está multiplicando o $x^{2}$ (ou qualquer que seja a incógnita que estiver elevada à 2), já o $b$ será o número que estiver multiplicando o $x$ , e por fim, o $c$ será o número solitário, que não estará multiplicando nenhuma variável.

Exemplo:

Considere a equação $x^{2} - 3 x + 2 = 0$ . Primeiro, identificamos os coeficientes:

$a = 1, b = - 3, c = 2$

Em seguida, podemos aplicar a fórmula de Bhaskara:

$x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$

$x = \frac{- (- 3) \pm \sqrt{(- 3)^{2} - 4.1 .2}}{2.1}$

$x = \frac{3 \pm \sqrt{1}}{2}$

Faremos dois cálculos, um considerando a raiz quadrada sendo somada e outro com a raiz sendo subtraída:

$x_{1} = \frac{3 + \sqrt{1}}{2}$

$x_{1} = \frac{3 + 1}{2}$

$x_{1} = \frac{4}{2}$

$x_{1} = 2$

$x_{2} = \frac{3 - \sqrt{1}}{2}$

$x_{2} = \frac{3 - 1}{2}$

$x_{2} = \frac{2}{2}$

$x_{2} = 1$

Portanto, as raízes da equação são $1$ e $2$ , isso significa que ao substituir um desses valores na equação $x^{2} - 3 x + 2 = 0$ , a igualdade vai se tornar verdadeira, ou seja, ficará $0 = 0$ .

Uma observação importante é que quem determina até quantas soluções podem ser obtidas para a equação é o grau dela, então, se ela for de grau $4$ , pode haver até quatro raízes que satisfazem a igualdade.

Como resolver uma equação de 2º grau incompleta?

De forma geral, é possível resolver as equações incompletas utilizando a fórmula de Bhaskara, mas há maneiras mais simples e rápidas para cada tipo.

Exemplo 1:

Resolva a equação $x^{2} - 9 = 0$

Quando o termo $b$ está faltando, basta isolarmos o $x^{2}$ :

$x^{2} = 9$

E depois aplicamos raiz quadrada em ambos os lados da equação para eliminarmos o expoente do $x$ e achar as raízes:

$\sqrt{x^{2}} = \sqrt{9}$

$x = \pm 3$

Consideramos tanto o valor positivo, quanto o negativo em raízes de índice par, pois ao resolvermos una equação, todos os valores possíveis que tornem a igualdade verdadeira são levados em conta, diferentemente de resolver uma raiz avulsa.

Exemplo 2:

Resolva a equação $x^{2} + 2 x = 0$

Quando o termo $c$ está faltando, colocamos $x$ em evidência:

$x (x + 2) = 0$

Para que uma multiplicação entre dois (ou mais termos) resulte em zero, um ou outro termo deve ser zero, portanto, temos duas possibilidades:

$x = 0$

$x + 2 = 0$

$x = - 2$

Então, as raízes para essa equação são $0$ e $- 2$ .

Exemplo 3:

Resolva a equação $2 x^{2} = 0$

Quando $b$ e $c$ estiverem faltando, basta isolar o $x^{2}$ :

$x^{2} = \frac{0}{2}$

$x^{2} = 0$

Em seguida, tiramos a raiz quadrada de ambos os lados:

$\sqrt{x^{2}} = \sqrt{0}$

$x = \pm 0$

Como o zero é um elemento neutro, ou seja, não possui sinal, é considerado somente $x = 0$

Método da Soma e Produto

O método da soma e produto é uma técnica alternativa para resolver equações de 2º grau, quando os coeficientes são números inteiros simples, como $1$ , $- 2$ , $3$ . Ela consiste em encontrar dois números que somados resultem em $\frac{- b}{a}$ e multiplicados resultem em $\frac{c}{a}$ , uma vez encontrado esses valores, parabéns, você encontrou as raízes da equação. Pode parecer complicado, mas aqui vai uma dica, geralmente, o coeficiente $a$ é igual à $1$ , quando isso acontecer, podes pensar da seguinte forma: Quais números que somados resultam em $- b$ e multiplicados resultam em $c$ ? Fica a seu critério utilizar esse método, mas saiba que sempre podes usar a boa e velha fórmula de Bhaskara para resolver qualquer equação de $2 °$ grau.

Exemplo:

Considere a equação $x^{2} - 5 x + 6 = 0$ . Precisamos encontrar dois números que somados dão $5$ e multiplicados dão $6$ . Esses números são $2$ e $3$ , pois $2 + 3 = 5$ e $2.3 = 6$ . Portanto, as raízes são $x = 2$ e $x = 3$ . Para comprovar se a resposta está correta, basta substituir os valores de $x$ na equação e verificar se a igualdade ficou verdadeira. Farei a verificação do $x = 2$ :

$x^{2} - 5 x + 6 = 0$

$2^{2} - 5.2 + 6 = 0$

$4 - 10 + 6 = 0$

$0 = 0$

O que está de um lado da equação é exatamente igual ao que está do outro lado, então $2$ é raiz da equação.

Exercícios resolvidos de equação de 2° grau

1. Dada a equação $x^{2} + 2 = - 2 x$ , encontre a solução, se existir

Primeiramente, vamos deixar ela na forma geral, para ajudar a encontrar quais são os coeficientes:

$x^{2} + 2 x + 2 = 0$

Identificamos os coeficientes e aplicamos a fórmula de Bhaskara:

$a = 1, b = 2, c = 2$

$x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$

$x = \frac{- 2 \pm \sqrt{(2)^{2} - 4.1 .2}}{2.1}$

$x = \frac{- 2 \pm \sqrt{- 4}}{2}$

O delta deu negativo, ou seja, não há solução para essa equação (pelo menos no conjunto dos números reais).

2. Uma empresa de jardinagem deseja construir um canteiro retangular em um parque. A área do canteiro deve ser de $8$ metros quadrados e o comprimento deve ser $2$ metros maior que a largura. Qual deve ser a largura do canteiro?

Para resolver essa questão, vamos definir a largura do canteiro como $x$ metros. O comprimento será $x + 2$ metros. A área do canteiro é dada pela multiplicação do comprimento pela largura:

$x (x + 2) = 8$

$x^{2} + 2 x = 8$

Podemos reorganizar a expressão para deixar na forma geral da equação de $2 º$ grau:

$x^{2} + 2 x - 8 = 0$

Agora aplicamos a fórmula de Bhaskara:

$a = 1, b = 2, c = - 8$

$x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$

$x = \frac{- 2 \pm \sqrt{(2)^{2} - 4.1 . (- 8)}}{2.1}$

$x = \frac{- 2 \pm \sqrt{36}}{2}$

Portanto, as soluções são:

$x_{1} = \frac{- 2 + \sqrt{36}}{2}$

$x_{1} = \frac{- 2 + 6}{2}$

$x_{1} = \frac{4}{2}$

$x_{1} = 2$

$x_{2} = \frac{- 2 - \sqrt{36}}{2}$

$x_{2} = \frac{- 2 - 6}{2}$

$x_{2} = \frac{- 8}{2}$

$x_{2} = - 4$

Como a largura não pode ser negativa, a largura do canteiro é $2$ metros.

Importância de aprender equação do 2º grau

A equação de $2 º$ grau aparece nos mais diversos assuntos, na física, por exemplo, elas são frequentemente utilizadas para descrever o movimento de objetos, calcular trajetórias e entender fenômenos naturais. No estudo de funções, essa equação ajuda a analisar e calcular valores importantes da função de $2 º$ grau.

Além disso, no cálculo, as técnicas aprendidas para resolver equações de $2 º$ grau são aplicadas em derivadas e integrais, que são ferramentas poderosas para modelar e resolver problemas complexos. Portanto, dominá-la é um passo importante para qualquer estudante que deseja aprofundar seus conhecimentos em matemática e não passar sufoco em matérias mais avançadas.

Daniel Duarte

Formado em Eletrotécnica pelo IFRN, além de ter cursos de Matemática Básica e Cálculo pela empresa Help Engenharia.

Sobre nós

O Matematiquês é um blog dedicado ao aprendizado de matemática, e nosso objetivo é tornar o ensino mais acessível e envolvente através de conteúdos de alta qualidade e gratuitos para alunos e professores em todo o Brasil. Buscamos simplificar conceitos complexos com uma abordagem clara e direta, priorizando transparência, diversidade, clareza, qualidade, inovação e compromisso social. Nosso blog oferece conteúdos fundamentados por especialistas, revisados com rigor e atualizados.

Categorias

Posts mais recentes

All Post
Curiosidades
Ensino Fundamental
Ensino Médio
Ensino Superior
Notícias

Back
Cinemática
Dinâmica
Conceitos básicos da física

Back
Conceitos básicos da matemática
Frações
Potenciação
Radiciação
Geometria plana
Logaritmo

Back
Funções
Equações
Conjuntos numéricos
Geometria espacial
Inequações
Módulo
Progressões matemáticas
Física
Trigonometria
Cinemática
Dinâmica
Conceitos básicos da física

Back
Limites
Derivadas
Integrais
Equações Diferenciais
Vetores e Geometria Analítica

Equação de 2º Grau: Guia Completo com Exemplos e Exercícios Resolvidos

O que é equação de 2º grau?

Equação de 2º grau completa

Equação de 2º grau incompleta

Coeficiente C igual à zero:

Coeficiente B igual à zero:

Coeficiente B e C iguais à zero:

Como resolver uma equação de 2º grau completa?

Delta maior que zero:

Delta igual a zero:

Delta menor que zero:

Como resolver uma equação de 2º grau incompleta?

Método da Soma e Produto

Exercícios resolvidos de equação de 2° grau

Importância de aprender equação do 2º grau

Sobre nós

Categorias

Posts mais recentes

Udesc abre inscrições para vestibular de inverno 2025!

Integrais por partes: Onde e como usar o método

Inscrições para Vestibular da Univesp Estão Para Acabar!

Tags

Matematiquês © 2024. Todos os direitos reservados.