Neste artigo, tentarei demonstrar de forma simples, construindo o raciocínio passo a passo, a relação entre os coeficientes angulares de duas retas perpendiculares (que formam um ângulo de
Demonstração da recíproca negativa entre coeficientes angulares de retas perpendiculares
Muitos de vocês já devem ter se deparado com a seguinte relação matemática: quando temos duas retas perpendiculares, o produto (multiplicação) entre seus coeficientes angulares é igual à
De outra forma, isso significa que o coeficiente de uma é o inverso oposto (recíproco negativo) do coeficiente da outra.
Mas afinal, qual a origem dessa relação? Onde podemos aplicá-la? Tentarei esclarecer essas dúvidas utilizando alguns conceitos da geometria e da trigonometria. Comecemos relembrando o conceito de reta: uma reta é uma linha formada por infinitos pontos um do lado do outro (pontos adjacentes). Podemos utilizar o plano cartesiano para representá-la.
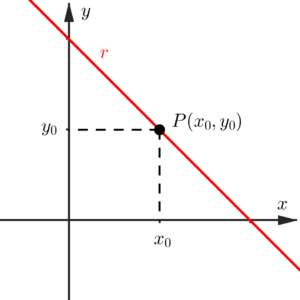
Temos na imagem acima uma reta
Um segmento (parte de um todo) de reta, por sua vez, é um pedaço limitado de uma reta, portanto, possui início e fim bem delimitados. Uma vez lembrados esses conceitos, conseguimos entender o que é um ângulo, que por definição, é a medida da abertura entre dois segmentos de reta que partem de um mesmo ponto (que possuem a mesma origem).
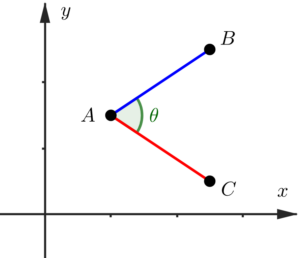
Acima temos os segmentos
Por sua vez, quanto maior for o ângulo, maior será a abertura entre eles.
Agora, seguindo essa linha de pensamento, vamos desenhar três pontos (

Podemos ligar os três pontos com segmentos de reta para formar uma figura fechada.
Note que podemos representar três ângulos dentro dessa figura, pois entre os segmentos
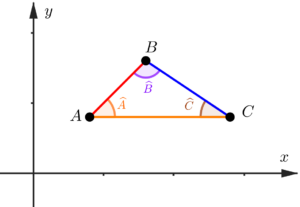
A figura acima, formada por três lados (segmentos) e três ângulos, é famoso “triângulo”, que é considerada por muitos a figura geométrica mais importante, pois de certa forma, qualquer outro polígono (figura fechada com três ou mais lados) pode ser transformado em triângulos. Uma vez construída a ideia de triângulo, podemos analisar um tipo de triângulo muito importante, o chamado triângulo retângulo (o nome retângulo se refere a um dos ângulos dele ser um ângulo reto, ou seja, que possui noventa graus).
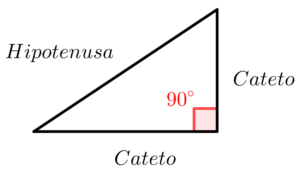
No triângulo retângulo, os lados adjacentes ao ângulo (que estão ao lado do ângulo) de noventa graus são chamados catetos e o lado oposto é a hipotenusa. Nomeando um dos ângulos faltantes de alpha (
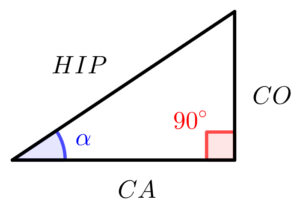
Partindo desse triângulo, existem três relações entre seus lados, chamadas “razões trigonométricas do triângulo retângulo”. A primeira delas é o seno, que é a divisão entre cateto oposto pela hipotenusa.
A segunda razão é o cosseno, que é a divisão do cateto adjacente pela hipotenusa.
E a terceira é a tangente (que será muito importante para o que queremos provar neste artigo), que é a divisão do cateto oposto pelo cateto adjacente.
Mas podemos reescrever a tangente como sendo seno dividido por cosseno:
Para os curiosos que querem saber o porquê da tangente ser seno sobre cosseno, segue abaixo a demonstração simplificada:
Nesse ponto do artigo, você que está lendo deve estar se perguntando: “O que tem haver a tangente de um triângulo retângulo com retas perpendiculares?”, é essa relação que estou tentando mostrar, e não falta muito para chegarmos nela. Podemos descrever matematicamente a reta, através de uma equação:
O
A partir daqui, caros leitores, tudo irá se encaixar, pois o valor do coeficiente angular é exatamente igual ao valor da tangente do ângulo formado entre a reta e o eixo horizontal (farei a demonstração disso em outro artigo, para não fugirmos muito do objeto de estudo deste artigo). Vamos pôr em prática os conceitos que mencionei até então, para demonstrar o porquê do coeficiente angular entre duas retas terem a relação que mostrei no início do artigo. Comecemos desenhando uma reta
Essa reta
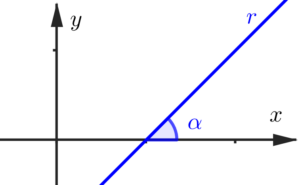
Representemos agora uma outra reta (que chamarei de
Essa reta
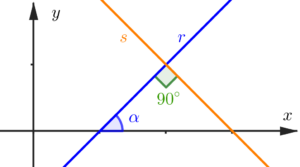
Vale ressaltar que a inclinação entre uma reta ou segmento de reta e a horizontal, é demarcado geralmente no sentido anti-horário, achei importante mencionar, pois algumas pessoas poderiam se perguntar o porquê dos ângulos sempre estarem à direita das retas, e não à esquerda. Dando continuidade, podemos demarcar três pontos interessantes nessa figura.
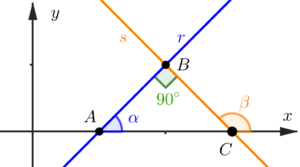
Olha só quem apareceu, um triângulo retângulo, formado entre os pontos
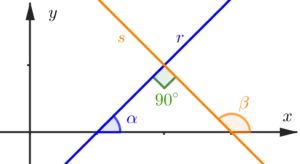
Recapitulando, o objetivo desse desenvolvimento todo é provar matematicamente que o coeficiente angular de uma reta qualquer
Só que sabemos que as tangentes dos ângulos formados entre essas retas e o eixo horizontal são iguais aos seus coeficientes angulares.
Portanto, a relação entre os coeficientes podem ser reescritos da seguinte forma:
Então, se de alguma forma, conseguirmos escrever as tangentes dos ângulos como na equação acima, provaremos a relação entre os coeficientes angulares de retas perpendiculares. Voltando para o desenvolvimento, chegamos na seguinte equação:
Em uma equação, podemos fazer tudo, contanto que façamos em ambos os lados dela (para que a igualdade seja mantida), portanto, podemos calcular a tangente de ambos os lados da equação.
Como vimos anteriormente, a tangente de um ângulo é igual ao seno dividido pelo cosseno desse mesmo ângulo.
Para calcular o seno e o cosseno da soma de dois ângulos quaisquer, utilizamos as seguintes equações (futuramente terá um artigo demonstrando de onde surgem essas equações da soma entre dois ângulos) :
Utilizando essas equações para o nosso problema, teremos:
O cosseno de
Se seno sobre cosseno é igual à tangente, o inverso disso, cosseno sobre seno, é igual ao inverso da tangente.
Já que as tangentes dos ângulos formados pelas retas
Aplicações da relação entre os coeficientes de retas perpendiculares
Podemos utilizar essa relação para acharmos a equação de uma reta que é perpendicular a outra em um ponto que conhecemos, pois o ponto de encontro entre as duas retas, seja ele qual for, pertencerá tanto a uma quanto à outra, e sabendo o coeficiente angular de uma, conseguimos determinar o coeficiente angular da outra.
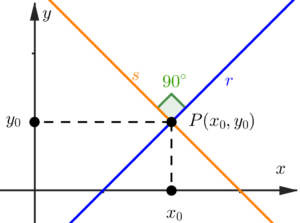
Em outras palavras, sabendo que o ponto
Outra aplicação interessante dessa relação é no cálculo das retas tangente e normal (retas que são perpendiculares entre si) à curva de uma função em um determinado ponto, juntamente com o conceito de derivada, é possível achar a equação de ambas.





