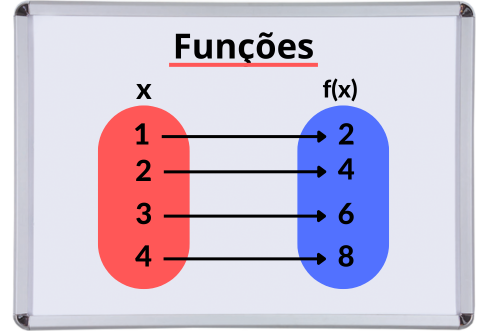
Um dos conceitos mais importantes da matemática e que gera muitas dúvidas a depender da forma que é explicado, a função é um artifício matemático poderoso e utilizado para diversas aplicações, desde entender o comportamento de uma bola ao ser lançada no ar, até como varia velocidade de um avião em determinada condição atmosférica. Além disso, esse assunto é a base para a famosa matéria chamada “cálculo”, que é vista em cursos de ensino superior que envolvem exatas.
O que é uma função?
De forma bem simplificada, é uma regra matemática que relaciona duas variáveis, dependendo do valor que uma delas assume, a outra assumirá um determinado valor.
Exemplo:
$$y=x+2$$
Na função acima, temos as letras $y$ e $x$, é comum que $y$ seja retratada como a variável dependente e o $x$ seja a variável independente, ou seja, o $y$ depende que o $x$ assuma determinado valor para que ele próprio assuma um valor. Vamos olhar o comportamento da função quando o $x$ for igual à $0$
$$y=x+2$$
$$y=0+2$$
$$y=2$$
A incógnita $y$ obteve o valor $2$, quando $x$ assumiu o valor $0$. E se ao invés de zero, o $x$ fosse $2$?
$$y=x+2$$
$$y=2+2$$
$$y=4$$
Notamos que o $y$ mudou, e à medida que o valor de $x$ for variando, o valor de $y$ irá variar também (há uma exceção, que explicarei posteriormente). Outra forma de representar a variável dependente é utilizando a simbologia $f()$, onde dentro do parênteses ficará a variável independente, nesse caso o $x$
$$f(x)=x+2$$
Nessa notação, é mais fácil visualizar qual a variável independente deve assumir, tomemos como exemplo $x$ assumindo os valores $1$ e depois $-2$
1)
$$f(x)=x+2$$
$$f(1)=1+2$$
$$f(1)=3$$
2)
$$f(x)=x+2$$
$$f(-2)=-2+2$$
$$f(-2)=0$$
Substituímos o valor que está dentro dos parênteses, em todo lugar que tiver a variável independente, como o $x$ no exemplo acima só aparece uma vez, só tivemos um lugar para substituir. Uma observação: Me limitarei nesse artigo a falar somente das funções de uma variável, para não acabar passando muita informação de uma vez só e acabar confundindo os leitores.
Definição matemática de função
Aquela foi a forma mais didática que consegui descrever a função, para que ficasse fácil o entendimento, no entanto, ela deixa de fora algumas especificidades, então irei explicar o conceito formal de função, assim como ele foi concebido pelos matemáticos.
A função é uma regra que relaciona valores de dois conjuntos numéricos (podendo eles serem iguais ou diferentes). O conjunto de valores que o $x$ pode assumir é chamado de domínio, e o conjunto de possíveis valores que o $f(x)$ pode assumir é denominado contradomínio. Caso a questão não especifique os conjuntos, assume-se que tanto domínio, quanto contradomínio são o conjunto dos números, ou seja, qualquer valor que pertença a ele, será valor um valor que ambas as variáveis podem assumir.
Só que, dependendo da função, quando substituirmos determinados valores para a variável dependente, chegaremos a um problema chamado “indeterminação matemática”, que é uma situação sem solução, e os valores que ocasionaram esse problema não farão parte do domínio da função. As indeterminações mais comuns são quando chegamos em um número dividido por zero, uma raiz de índice par de um número negativo ou um logaritmo que possui o logaritmando que não respeite suas próprias condições de existência.
Exemplo 1:
Determine o domínio da função abaixo
$$f(x)=2x$$
Nesse tipo de questão, é importante nos atentarmos as possíveis situações que possam resultar em indeterminações, para então definirmos o que foi pedido. Bom, não temos uma fração, portanto, não há como substituirmos um valor para $x$ e resultar em uma divisão por zero, não há logaritmo e muito menos raiz, então, o domínio é o conjunto dos números reais. E o contradomínio? Não há restrições em relação ao contradomínio, então, assumimos que ele é o conjunto dos números reais. O jeito formal de descrever o domínio de uma função é:
$$D(f)={x\,\epsilon\,\mathbb{R}}$$
Podemos ler essa sentença como “O domínio da função $f$ é definido por valores de $x$ pertencentes ao conjunto dos números reais”, e de forma abreviada: “Domínio de $f$, tal que $x$ pertence aos reais”.
Exemplo 2:
Determine o domínio e a imagem da função abaixo
$$f(x)=x^2$$
Não há nenhuma restrição em relação ao domínio, pois não há nada que possa causar uma indeterminação, porém, nos é pedida a imagem da função, que significa os valores de $f(x)$ para essa função em específico, em muitas ocasiões a imagem será igual ao contradomínio, mas precisamos ficar atentos, pois nem sempre será assim. Percebes que o $x$ (variável dependente), está sendo elevada ao quadrado? Uma característica importante de valores que são elevados ao quadrado, é que independentemente se ele é positivo ou negativo, ao ser elevado à $2$, o resultado será sempre positivo, vamos fazer alguns testes.
1)
$$f(x)=x^2$$
$$f(3)=3^2=9$$
2)
$$f(x)=x^2$$
$$f(-2)=x^2$$
$$f(-2)=(-2)^2=4$$
3)
$$f(x)=x^2$$
$$f(-\frac{1}{2})=(\frac{-1}{2})^2=\frac{1}{4}$$
Ou seja, não importa se o valor que $x$ assume seja positivo ou negativo, o resultado (valor de $y$ ou $f(x)$, como preferir chamar) será positivo, portanto, o conjunto imagem será o conjunto dos números reais positivos, incluindo o zero.
$$D(f)={x\,\epsilon\,\mathbb{R}}$$
$$Im(f)=\mathbb{R_{+}}$$
Exemplo 3:
Determine o domínio e a imagem da função abaixo
$$f(x)=\frac{2}{x-3}$$
Nesse caso, temos a variável no denominador, portanto, para algum valor de $x$, poderá ocorrer uma indeterminação. Como descobrimos o valor que o $x$ não deve assumir? Montamos uma inequação, onde teremos toda a expressão do denominador, diferente de zero, e então isolamos a variável
$$x-3\neq0$$
$$x\neq3$$
O $x$ mão pode assumir o valor $3$, portanto, dizemos que $3$ não está no domínio da função. Em relação a imagem, ela é todo o conjunto dos números reais com exceção do zero, pois o numerador é $2$ mesmo que façamos a divisão por qualquer outro número, o resultado nunca será zero.
$$D(f)={x\,\epsilon\,\mathbb{R}/x\neq3}$$
$$Im(f)=\mathbb{R}\setminus\{0\}$$
Vamos conferir se realmente há indeterminação para o valor que encontramos
$$f(x)=\frac{2}{x-3}$$
$$f(3)=\frac{2}{3-3}$$
$$f(3)=\frac{2}{0}$$
Há duas considerações importantes a serem feitas, primeiro, a imagem não pode ser maior que o contradomínio, em outras palavras, o conjunto imagem deve conter a mesma quantidade ou menos elementos que o contradomínio. Segundo, mais de um valor de $x$ pode resultar em um único valor de $y$, no entanto, caso um valor de $x$ resulte em mais de um valor de $y$, a sentença matemática não será uma função. A visualização disso será melhor com os diagramas de flechas (uma representação muito usada para representar conjuntos) abaixo.
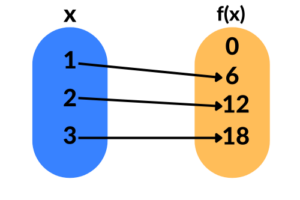
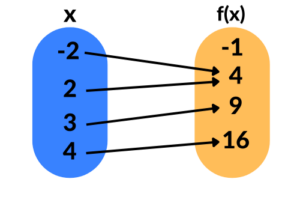
Na imagem acima, temos uma função, pois os valores de $x$ se relacionam com valores distintos de $f(x)$
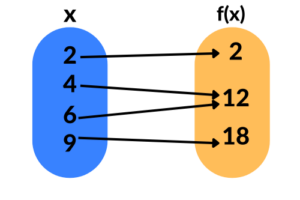
Nesse caso também temos uma função, pois não há problema em dois valores de $x$ estarem sendo relacionados a um mesmo valor de $f(x)$
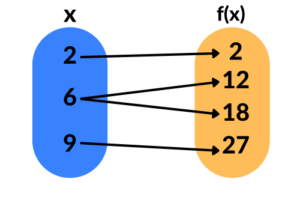
Já nessa última imagem, não temos uma função, pois para um mesmo valor de $x$, estão relacionados dois valores de $f(x)$
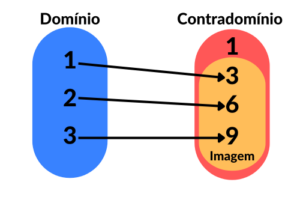
Por fim, mas não menos importante, acima podemos ver a representação dos três tipos de conjuntos abordados nas funções, e especificamente nesse exemplo a imagem possui menos elementos que o contradomínio.
Classificações da função
As funções podem ser classificadas em relação a como os conjuntos domínio, imagem e contradomínio se relacionam, podendo ser quatro os tipos.
Função sobrejetora:
É quando uma função possui o conjunto imagem igual ao contradomínio, ou seja, para todo valor de $y$ há pelo menos um valor de $x$ correspondente.
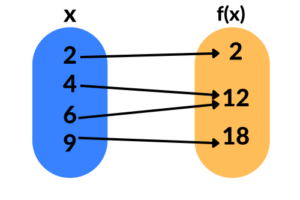
Exemplo:
$f(x)=x-1$
Função injetora:
Todos os elementos do domínio possuem correspondentes únicos no contradomínio, em outras palavras, para cada valor de $x$, há um único valor de $y$ correspondente.
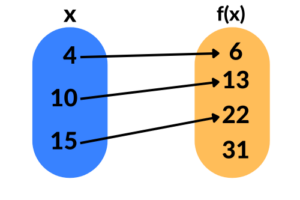
Exemplos:
1) $f(x)=x+2$
2) $f(x)=3x$
Função bijetora:
É uma função que é injetora e sobrejetora ao mesmo tempo, ou seja, além do conjunto imagem ser igual ao contradomínio, para cada valor de $x$, há apenas um correspondente para $y$
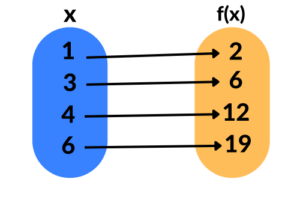
Exemplos:
1) $f(x)=2x+3$
2) $f(x)=x$
Função simples:
Sendo o extremo oposto da anterior, uma função é classificada como simples quando não é nem injetora nem sobrejetora
Exemplo:
$f(x)=x^2$
Gráfico de uma função
A fim de entendermos melhor o comportamento da função para os inúmeros valores da variável independente, utilizamos o plano cartesiano ao nosso favor. Representamos cada par ordenado com os valores correspondentes das variáveis $x$ e $y$, como um ponto no plano, e a junção de infinitos pontos dará origem um gráfico, uma representação visual dos valores que relacionamos na função.
Exemplo:
Função: $f(x)=-x+2$
Gráfico:
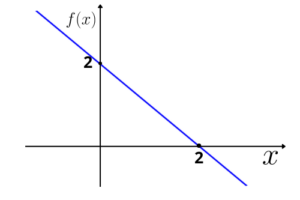
Os pontos em que o gráfico toca os eixos $f(x)$ e $x$ são chamados “pontos de intersecção”, e achá-los é o primeiro que devemos fazer para começarmos a montar o gráfico de uma função.
Tipos de funções
A função também pode ser classificada de acordo com o tipo de expressão que aparece nela, são vários os tipos, tantos quantos os tipos de equação.
Função linear:
A função de $1°$ grau (também chamada de função afim), possui um polinômio de grau $1$.
Exemplo:
$f(x)=x+5$
Gráfico padrão:
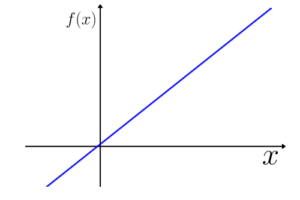
Função quadrática:
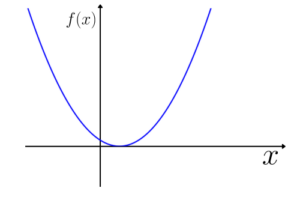
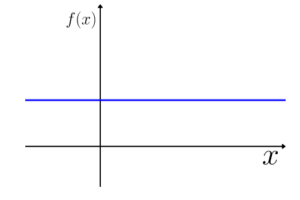
Função constante:
A função constante não possui variável independente, tendo apenas uma constante como expressão.
Exemplo:
$f(x)=8$
Gráfico padrão:
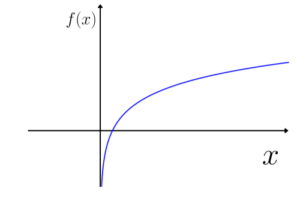
Função logarítmica:
A função logarítmica possui ao menos um logaritmo na expressão.
Exemplo:
$f(x)=log_{2}x$
Gráfico padrão:
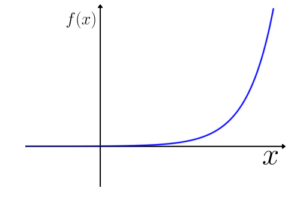
Função exponencial:
A função exponencial possui ao menos um número elevado à variável independente.
Exemplo:
$f(x)=3^x$
Gráfico padrão:
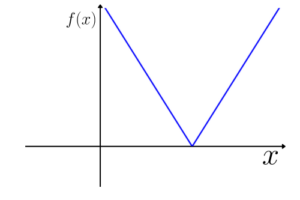
Função modular:
A função modular possui pelo menos um dos termos que tem a variável independente, dentro de um módulo.
Exemplo:
$f(x)=|x-2|$
Gráfico padrão:
Função trigonométrica:
A função trigonométrica possui pelo menos uma razão trigonométrica, podendo ser seno, cosseno, tangente ou suas inversas.
Exemplo:
$f(x)=sen(5x)$
Gráfico da função seno:
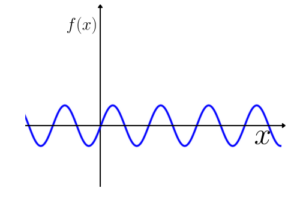
Função racional:
A função racional possui uma fração cuja variável independente se encontra em seu denominador.
Exemplo:
$f(x)=\frac{5}{x-1}$
Gráfico padrão:
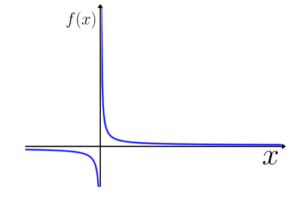
Função irracional:
A função irracional possui a variável independente dentro de alguma raiz.
Exemplo:
$f(x)=\sqrt{-x+7}$
Gráfico padrão:
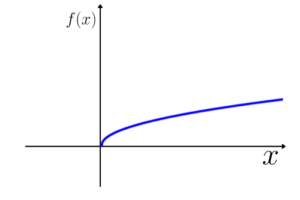
Função par:
É uma função que caso substitua um valor e seu oposto, o resultado será o mesmo, de outra forma: $f(x)=f(-x)$
Exemplo:
$f(x)=x^2$
Função ímpar:
Ao contrário da função par, os valores encontrados para a $f(x)$ irão ser diferentes para $x$ e seu oposto, ou seja: $f(-x)=-f(x)$
Exemplo:
$f(x)=x^3$
Função inversa:
Função inversa é o nome dado a funções que possuem o comportamento invertido em relação a outra função, por exemplo: As funções logarítmica e exponencial são inversas, assim como as funções cosseno e secante.
Exemplo:
Se a função é $f(x)=2^x$, a função inversa será $f^{-1}(x)=log_{2}(x)$
Função composta:
A função composta é uma junção de duas ou mais funções, que quando combinadas podem produzir um comportamento único.
Exemplo:
Dadas as funções $f(x)=x^2$ e $g(x)=x+1$, a função composta $f(g(x))$ será $f\circ g=(x+1)^2$
Tudo que você aprendeu com “x” serve para outras letras
Muitas pessoas ficam com dúvida quando se deparam com questões que não possuem $f(x)$, $y$ ou $x$, e acabam por não saberem o que fazer, pois quando lhes foi ensinado o assunto de funções, os exemplos utilizavam essas letras e símbolo, no entanto, venho aqui para te informar que independentemente das variáveis envolvidas, tudo o que você aprendeu sobre funções, será utilizado da mesma forma.
Exemplo:
Determine o domínio e a imagem da função abaixo
$f(z)=z^2$
A função acima possui como variável independente, a letra $z$ e a variável dependente é $f(z)$ (que pode ser chamado de qualquer outra letra que não seja $z$), seu domínio será o conjunto dos números reais e a imagem será os reais positivos
$$D(f)={z\,\epsilon\,\mathbb{R}}$$
$$Im(f)={z\,\epsilon\,\mathbb{R_{+}}}$$
Notou como a notação acima mudou? Pois a variável não é $x$ nessa ocasião, e sim a letra $z$.
Exercícios resolvidos de função
1. Considere a função quadrática $f(x)=x^2-4x+5$. Calcule o valor de $f(x)$ quando $x=1$ e $x=-1$.
Para resolvermos essa questão, basta substituirmos os valores de $x$ na função que nos foi dada e realizar as operações até restar um único valor.
1)
$f(x)=x^2-4x+5$
$f(1)=1^2-4.1+5=1-4+5=2$
2)
$f(x)=x^2-4x+5$
$f(1)=(-1)^2-4.(-1)+5=1+4+5=10$
2. Determine a lei da função $f(x)=3x$.
A lei de formação (ou lei da função) se trata da descrição de como os valores do domínio se relacionam com os valores do contradomínio. Na função acima, os valores de $f(x)$ serão o triplo dos valores que $x$ assumir.
Formado em Eletrotécnica pelo IFRN, além de ter cursos de Matemática Básica e Cálculo pela empresa Help Engenharia.
