Não tão conhecida, ela é um caso particular de função, que possui poucas aplicações, mas é interessante conhecê-la, pois há problemas de física que envolvem esse tipo de função.
O que é uma função constante?
Basicamente, é uma função que não possui variação, pois independentemente do valor que a variável independente assume, o valor de
Exemplos:
1)
2)
3)
Sua forma geral é dada por:
Onde “k” é um número qualquer, que pertence ao conjunto dos números reais (geralmente). Uma característica interessante dessa função é que o conjunto imagem possui apenas um elemento, que é justamente a constante “k”.
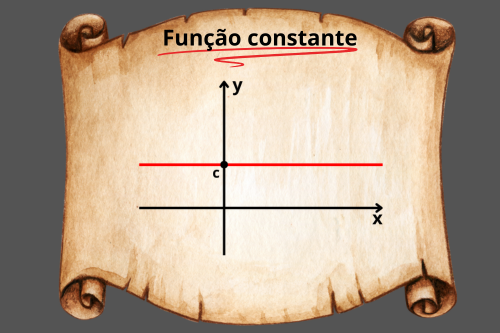
Gráfico da função constante
O formato do gráfico da função constante é uma reta paralela ao eixo
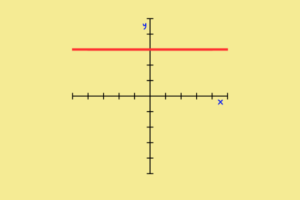
Como fazer o gráfico da função constante?
É a coisa mais fácil do mundo desenhar o gráfico dela, pois será uma reta na horizontal que corta (intersecta) o eixo
Exemplo:
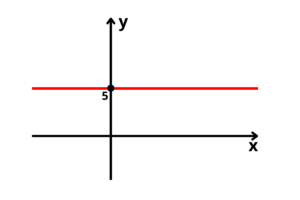
Desenhe o gráfico da função
O ponto em que o gráfico irá intersectar o eixo
Exercícios resolvidos de função constante
1. Qual das funções abaixo é constante?
a)
b)
c)
A primeira função é linear, e a depender do valor de
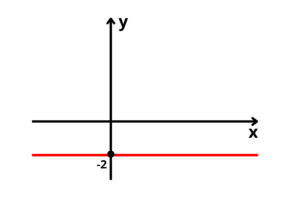
2. Crie o gráfico da função
O gráfico será uma reta horizontal que intersecta o eixo
Já que a questão não deu nenhuma restrição quanto ao conjunto que deve ser adotado, podemos deduzir que o domínio é todo o conjunto dos números reais e a imagem é apenas o elemento
Formado em Eletrotécnica pelo IFRN, além de ter cursos de Matemática Básica e Cálculo pela empresa Help Engenharia.
