Irei tentar mostrar e explicar o porquê da derivada também ser chamada de “inclinação da função”. Para isso, preciso relembrar alguns conceitos de trigonometria e geometria. Tomemos um triângulo retângulo qualquer:
Desenhando um ângulo
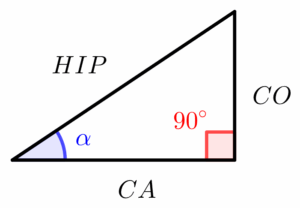
A tangente desse ângulo, será igual ao cateto oposto dividido pelo cateto adjacente.
Mais precisamente, estaremos dividindo o comprimento dos catetos. Mas afinal, o que a tangente representa? Ao calcularmos essa divisão entre os catetos, o que o valor obtido nos diz? Vamos pegar três triângulos retângulos, com ângulos notáveis, e analisar o valor de suas tangentes, comparando o resultado com os próprios triângulos.
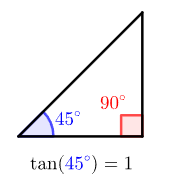
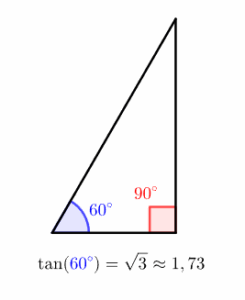
Na medida em que o ângulo aumenta, o valor da tangente também aumenta. Isso não é coincidência, pois ter uma abertura angular maior, significa que o cateto oposto aumentou ou o cateto adjacente diminuiu de tamanho (comprimento), e pela tangente ser a divisão entre ambos, quanto maior o resultado da divisão, maior será o ângulo entre os catetos, e quanto menor a tangente, menor a abertura. Uma vez entendida essa ideia, vamos olhar o gráfico de uma função de
Essa reta forma um ângulo (que chamarei de
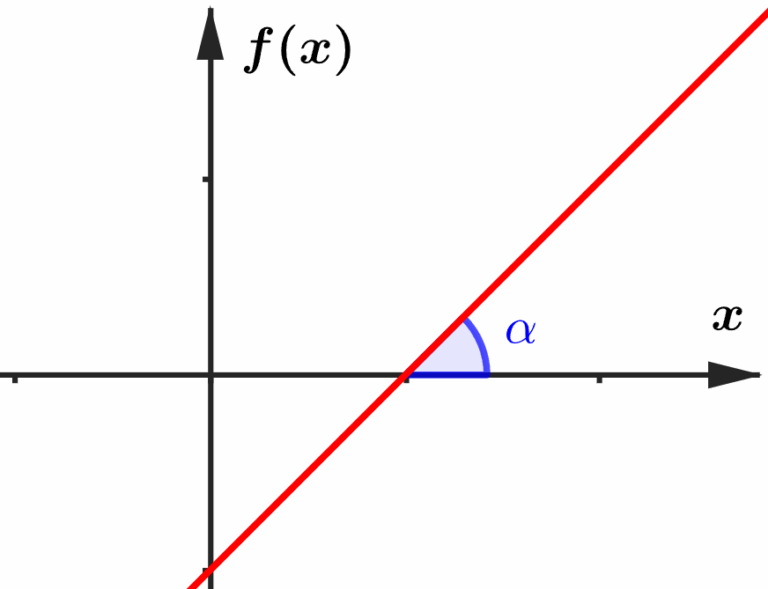
Quanto maior for o ângulo, maior a inclinação da reta, e quanto menor o ângulo, menor é sua inclinação. Olha que curioso, acabamos de ver um conceito da trigonometria, cujo resultado nos indica o quão aberto um ângulo está, e na função linear acima, o tamanho do ângulo dela em relação ao eixo horizontal, indica a inclinação dela, parecem a mesma coisa não é? Sim, a tangente desse ângulo é igual à inclinação da função, ou seja, calcular a tangente dele nos indicará quão inclinado o gráfico está. Vou além, uma reta possui uma equação que a define, chamada “equação da reta”, e ela tem a seguinte forma:
O
E podemos calcular o
Pegamos dois valores de
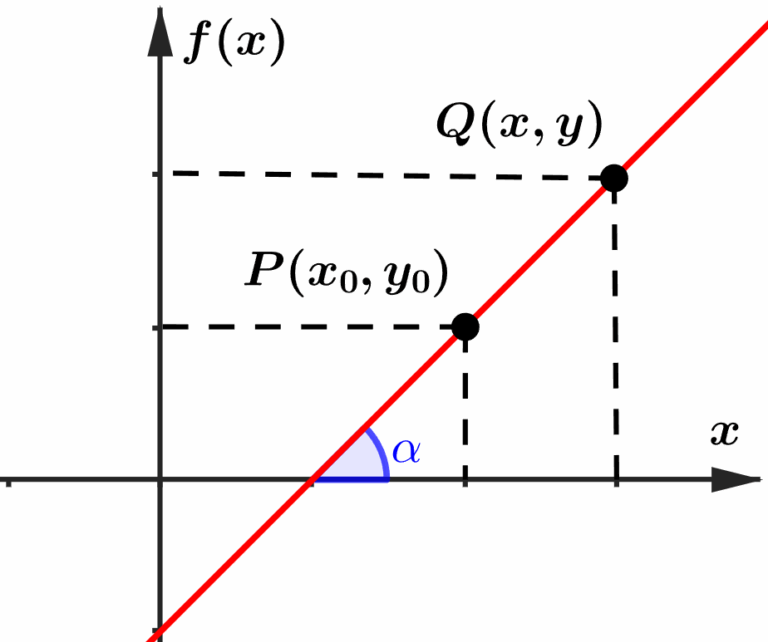
Note que se ligarmos os pontos
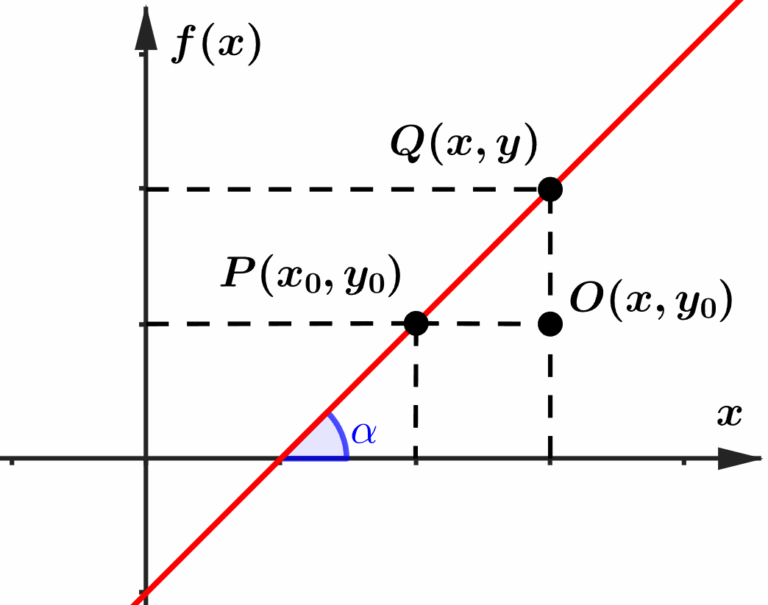
Não está conseguindo visualizar? Irei demarcar com mais ênfase o triângulo na imagem.
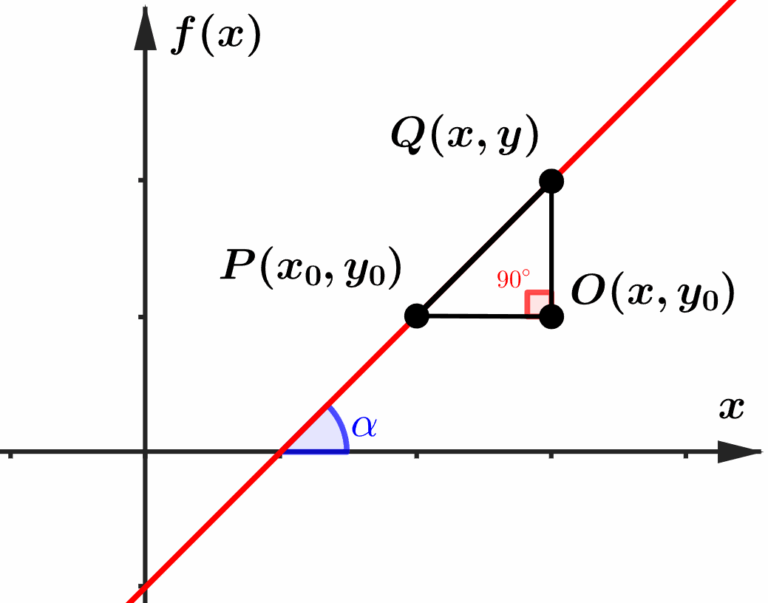
Perceba que o ângulo formado no canto esquerdo do triângulo retângulo, é exatamente igual ao ângulo formado entre a reta e o eixo
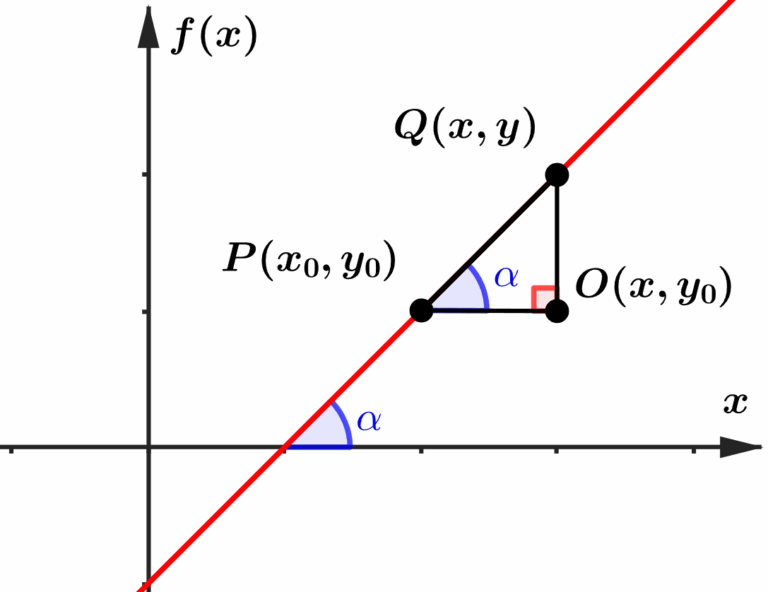
Portanto, se calcularmos a tangente desse ângulo
Olha só quem apareceu naturalmente na expressão, o coeficiente angular.
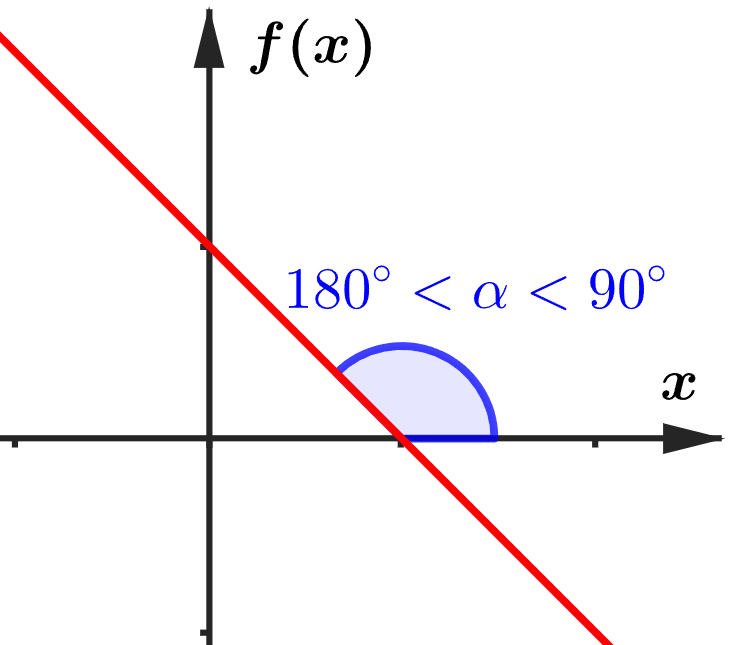
Vale ressaltar, que inclinação e valor do ângulo são coisas diferentes, a inclinação é um parâmetro que nos informa indiretamente o tamanho do ângulo, já o valor do ângulo é o tamanho exato da abertura (suas unidades são graus e radianos). Outra coisa importante a ser mencionada, é que quando o coeficiente angular (inclinação) é positivo, a reta é crescente, e quando ele é negativo, a reta é decrescente (isso significa que o ângulo formado em relação à horizontal é
Vamos tentar extrapolar essa ideia para uma função qualquer, e para isso, utilizarei como exemplo uma função de segundo grau.
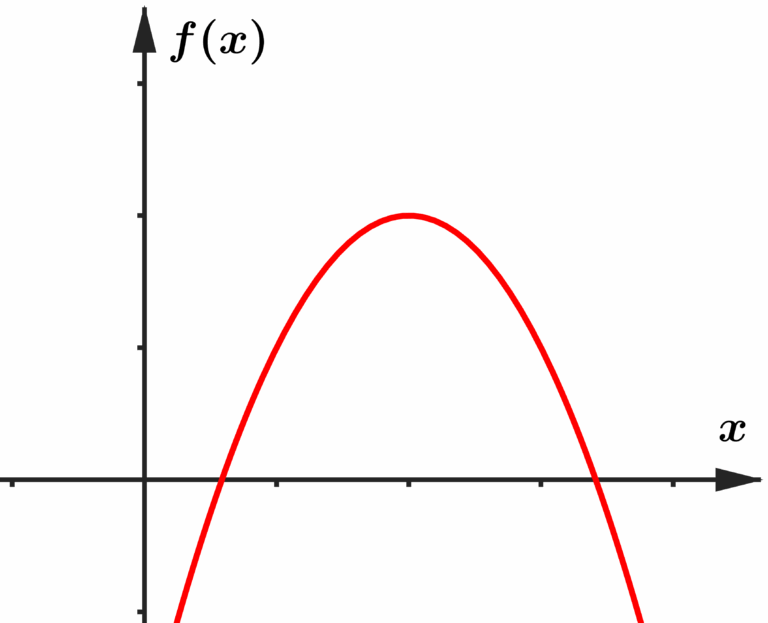
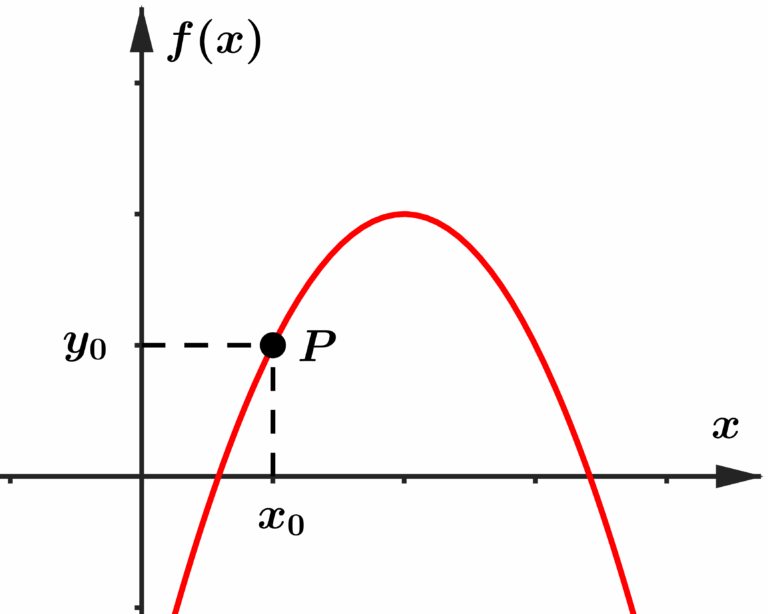
Temos acima o gráfico de uma função quadrática qualquer, agora eu te pergunto, como poderíamos calcular a inclinação dessa função? Concorda comigo que ela não possui uma inclinação única? Pois diferentemente de uma reta, que possui sempre a mesma inclinação, essa parábola começa crescendo, depois atinge um pico, e começa a decrescer. Então, o melhor que poderíamos fazer, é descobrir a inclinação dessa função em um único ponto. Expandindo nossa ideia de inclinação para um conceito mais preciso, a inclinação de uma função qualquer em um determinado ponto, diz respeito ao ângulo formado entre uma reta tangente a função nesse mesmo ponto.
Mas o que é uma reta tangente? De forma simplificada, é uma reta que toca o gráfico em um único ponto, mas faz isso de forma muito sutil. Escolhendo um ponto
A reta tangente a esse ponto
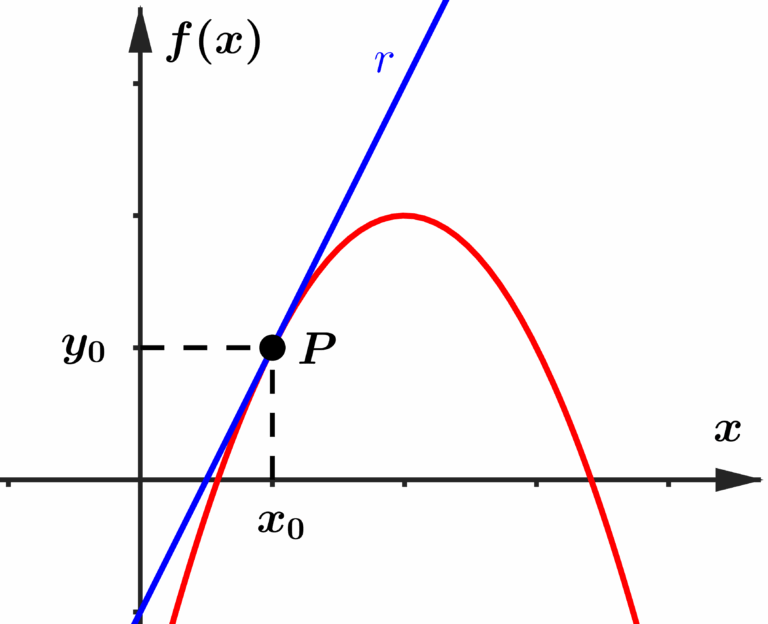
Descobrir o coeficiente angular dessa reta, nos dará a inclinação dessa função no ponto
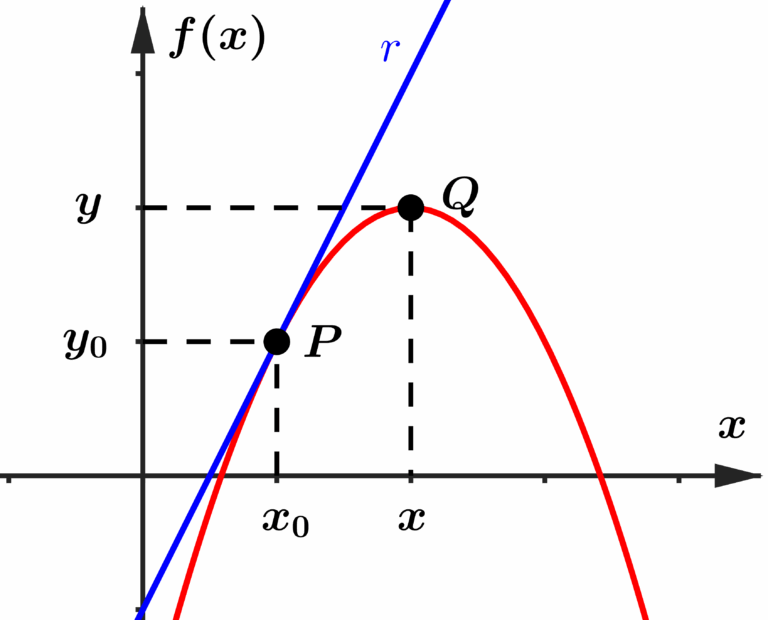
Podemos traçar uma reta que corta o gráfico nesses dois pontos (irei chamar essa reta de
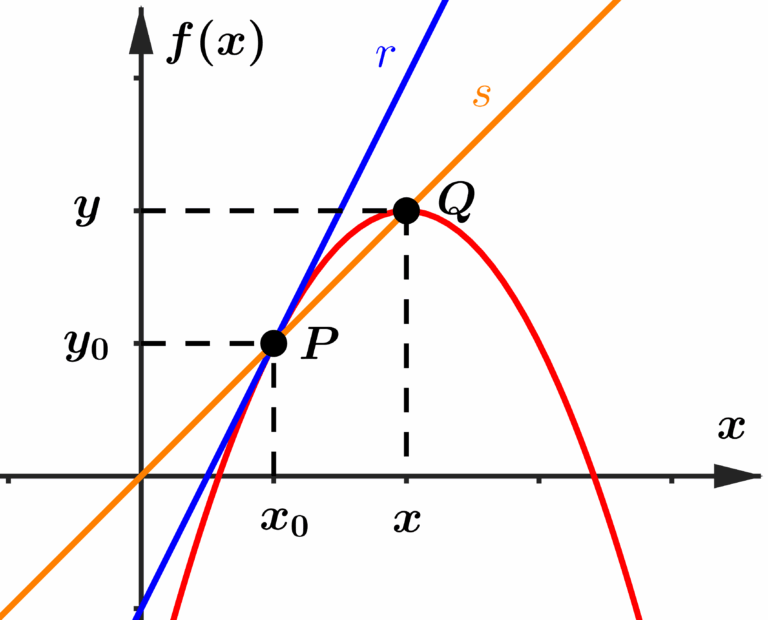
Perceba que a reta secante possui inclinação diferente da reta tangente. Mas o que aconteceria se aproximássemos um pouco o ponto
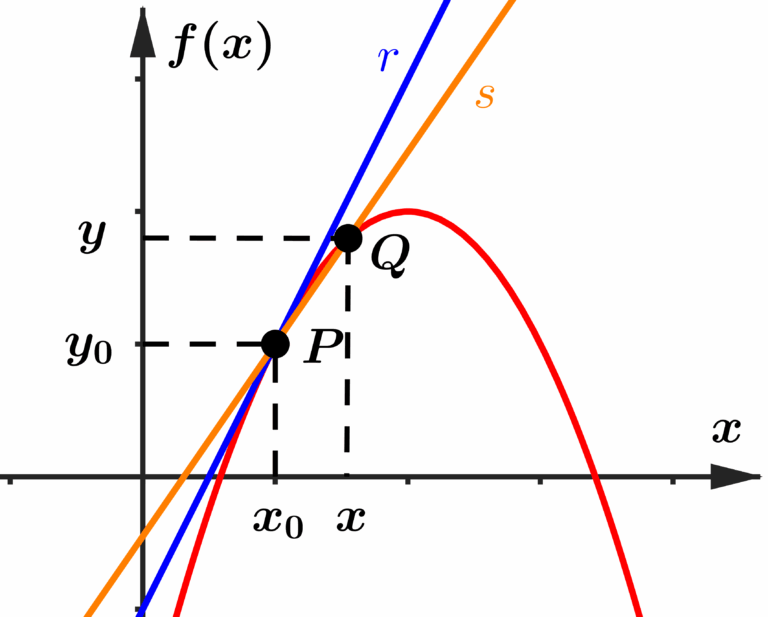
A reta secante ficou com uma inclinação maior, se aproximando um pouco da inclinação da reta tangente. Vamos aproximar mais o
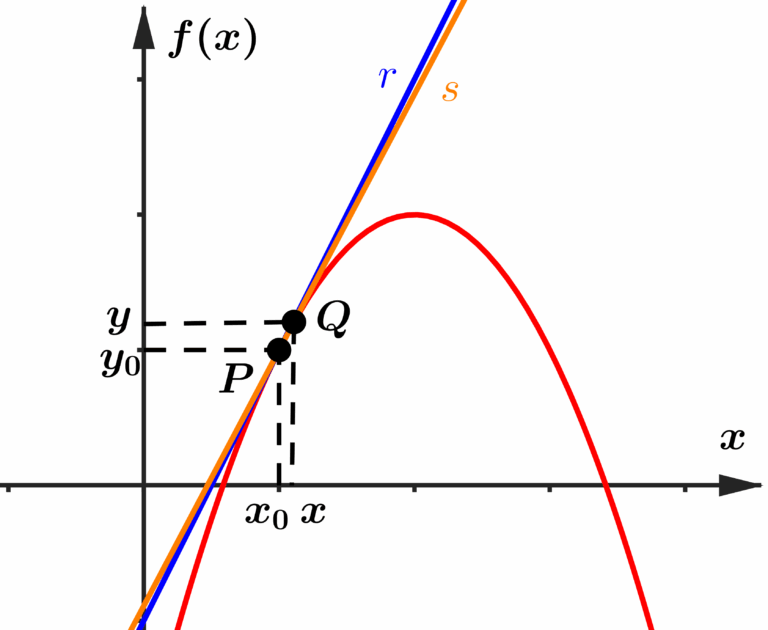
As retas estão praticamente sobrepostas na situação acima, o que nos leva a concluir que se o
Sendo
A expressão acima te lembra alguma coisa? Deixa eu reescrevê-la, chamando
Tanto essa expressão, quanto a anterior, representam a mesma coisa, o coeficiente angular da reta tangente à curva da função em um ponto é igual à derivada da função nesse mesmo ponto. Em outras palavras, a derivada nos dá a inclinação da função em um ponto.
Formado em Eletrotécnica pelo IFRN, além de ter cursos de Matemática Básica e Cálculo pela empresa Help Engenharia.
