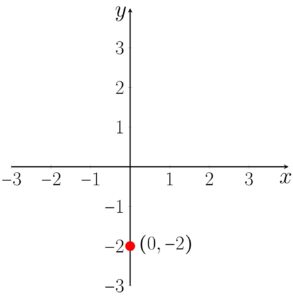Muito utilizados em vetores e mencionados quase sempre em questões envolvendo o plano cartesiano, os pares ordenados são ferramentas úteis para representar determinadas informações na matemática.
O que é um par ordenado?
Nada mais, nada menos, um par ordenado é uma representação matemática de dois elementos de um conjunto numérico, coordenadas de um vetor ou de um ponto em um plano cartesiano. O nome “ordenado” não foi dado por acaso, pois a ordem dos elementos importam, por exemplo, o par
Exemplos:
1)
2)
3)
Podemos simbolizar o par ordenado em um parêntese, com dois elementos um do lado do outro, separados por uma vírgula, e cada um deles representa um valor específico.
O valor que fica na posição do
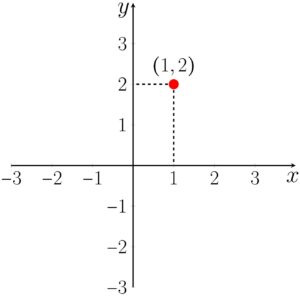
Como representar o par ordenado no plano cartesiano?
Para marcarmos um ponto no plano cartesiano, precisamos de duas coordenadas, uma para o eixo
Em geral, para qualquer ponto, teremos a seguinte forma:
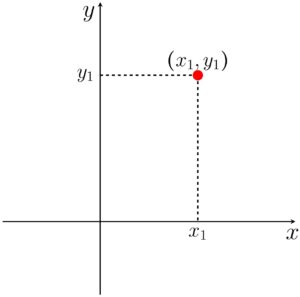
Onde o valor de
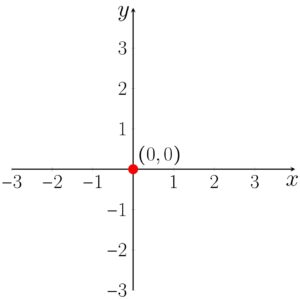
Par ordenado nas funções
O par ordenado também pode representar o valor da variável independente e o valor correspondente da variável dependente.
Exemplo:
Calcule
O valor da nossa variável independente será
Podemos representar essa dupla de valores no par ordenado
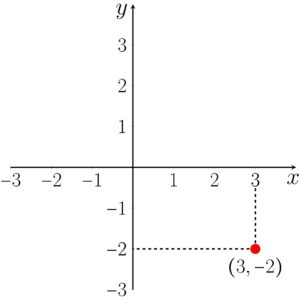
Exercícios resolvidos de par ordenado
1. Represente no plano cartesiano o ponto de coordenadas
O primeiro elemento corresponde ao valor no eixo
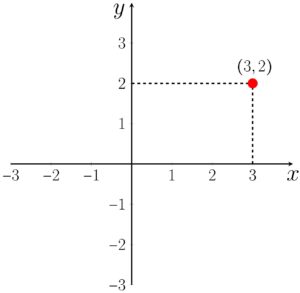
2. Em uma determinada função
O primeiro elemento do par será
Formado em Eletrotécnica pelo IFRN, além de ter cursos de Matemática Básica e Cálculo pela empresa Help Engenharia.
