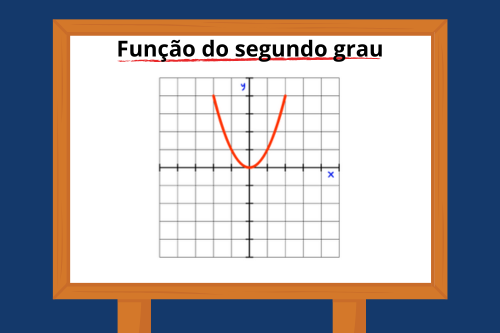
Provavelmente a função de 2° grau é a mais conhecida das funções, ela é marcante por causa do formato de seu gráfico e suas aplicações, sendo capaz de descrever a trajetória de alguns objetos e até mesmo analisar o valor máximo de lucro que um capital pode atingir.
O que é uma função de 2° grau?
A função quadrática, como é chamada, é uma função polinomial que possui um polinômio de grau $2$, em outras palavras, o maior grau da variável independente é $2$.
Exemplos:
1) $f(x)=x^2-2x+3$
2) $f(x)=x^2+x$
3) $f(x)=-2x^2$
Sua forma geral é dada por:
$$f(x)=ax^2+bx+c$$
Sendo $a$, $b$ e $c$ números quaisquer, pertencentes na maioria dos casos ao conjunto dos números reais, e $a$ deve ser diferente de zero. Caso o $a$ seja zero, teremos uma função linear, e se tanto o $a$ quanto o $b$ forem zero, cairemos em uma função constante. Uma curiosidade sobre o nome dela é que o termo “quadrática” se dá ao fato de uma das variáveis (a de maior grau) estar elevada à $2$, portanto, estar “elevada ao quadrado”.
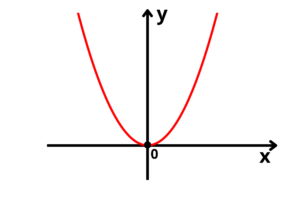
Gráfico da função de 2° grau
O formato do gráfico da função quadrática é uma parábola, uma curva que começa crescendo e ao chegar em certo ponto, passa a decrescer (ou o contrário).
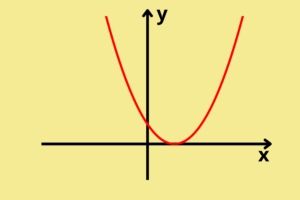
Como fazer o gráfico da função de 2° grau?
De forma parecida com a que abordamos a construção do gráfico da função de $1°$ grau, precisaremos descobrir em quais pontos o gráfico intersecta os eixos coordenados (eixos $x$ e $y$), só que há um elemento há mais que precisamos calcular, o chamado “vértice da parábola”, que é o ponto em que ela muda seu comportamento.
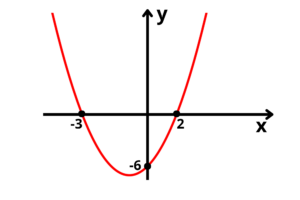
Raízes da função de 2° grau:
Para achar o ponto de intersecção da parábola com o eixo $y$, precisamos zerar a variável dependente (nesse artigo será o $x$), ou basta olharmos para o termo que não estiver multiplicando o $x$. Já a intersecção com o eixo $x$ pode acontecer em um único ponto, em dois ou nenhum, essa variedade de possibilidades se dá pela presença de um polinômio de segundo grau. Para acharmos esses pontos, precisamos zerar o $f(x)$ e resolver a equação de $2°$ grau que irar surgir. As raízes da equação demarcarão justamente os pontos em que o gráfico intersecta o eixo horizontal (eixo $x$).
Vértice da parábola:
Tão importante quanto os pontos de intersecção com os eixos, para desenharmos o gráfico de uma função quadrática precisamos encontrar o vértice da parábola, e para isso utilizamos duas fórmulas que nos darão as coordenadas $x$ e $y$ do ponto que representa o vértice no plano cartesiano. Esse ponto é chamado ponto de máximo ou mínimo, pois demarca o maior ou menor valor que a função irá alcançar.
X do vértice:
$$x_v=\frac{-b}{2a}$$
Y do vértice:
$$y_v=\frac{-\Delta}{4a}$$
Essas letras são os coeficientes da função: $f(x)=ax^2+bx+c$, e o delta (triângulo) é o discriminante encontrado ao achar as raízes da equação.
Exemplo:
Determine o gráfico da função $f(x)=x^2+x-6$
Primeiramente, devemos zerar o $x$ para achar o ponto de intersecção com o eixo $y$
$$f(x)=x^2+x-6$$
$$f(0)=0^2+0-6$$
$$f(0)=-6$$
Não precisaríamos realizar esse processo, bastava olhar para a constante $-6$, mas é sempre bom saber mais de um método. O processo para achar o(s) ponto(s) de intersecção com o eixo $x$ começa por zerarmos o $f(x)$
$$f(x)=x^2+x-6$$
$$0=x^2+x-6$$
Caímos em uma equação de segundo grau completa, e ao resolvermos ela através de Bháskara, intersecção com o eixo $x$
$$0=x^2+x-6$$
$$x^2+x-6=0$$
$$a=1,b=1,c=-6$$
$$x=\frac{-b\pm\sqrt{∆}}{2a}$$
$$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$$
$$x=\frac{-1\pm\sqrt{1^2-4.1.(-6)}}{2.1}$$
$$x=\frac{-1\pm\sqrt{1+24}}{2}$$
$$x=\frac{-1\pm\sqrt{25}}{2}$$
$$x=\frac{-1\pm5}{2}$$
$$x_1=\frac{-1+5}{2}=\frac{4}{2}=2$$
$$x_2=\frac{-1-5}{2}=\frac{-6}{2}=-3$$
Temos duas raízes, portanto, o gráfico toca o eixo $x$ em dois pontos: $(-3,0)$ e $(2,0)$. Agora vamos encontrar as coordenadas do vértice, utilizando as fórmulas mostradas anteriormente
X do vértice:
$$x_v=\frac{-b}{2a}=\frac{-1}{2.1}=\frac{-1}{2}=-0,5$$
Y do vértice:
$$y_v=\frac{-∆}{4a}=\frac{-25}{4.1}=\frac{-25}{4}=-6,25$$
Agora podemos desenhar o gráfico da função
Tipos de parábolas da função de 2° grau
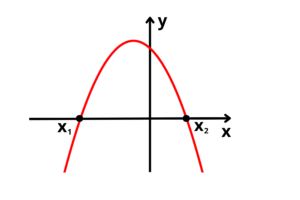
Há seis tipos de formas que a parábola poderá ser encontrada, o que vai determinar isso serão as raízes da função e o sinal do coeficiente $a$, pois se ele for positivo a concavidade estará voltada para cima e vértice será um ponto de mínimo, e se for negativo a concavidade ficará voltada para baixo, com o vértice indiciando um ponto de máximo.
Duas raízes reais e distintas (“a” positivo):
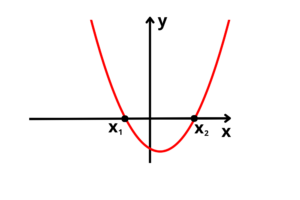
Duas raízes reais e distintas (“a” negativo):
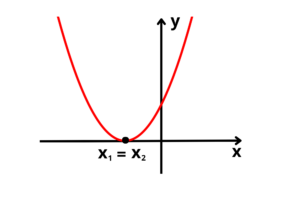
Duas raízes reais e iguais (“a” positivo):
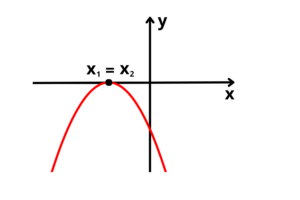
Duas raízes reais e iguais (“a” negativo):
Nenhuma raiz real (“a” positivo):
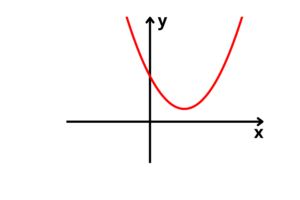
Nenhuma raiz real (“a” negativo):
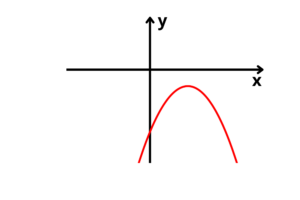
Exercícios resolvidos de função de 2° grau
1. Plote o gráfico da função $f(x)=x^2$
“Plotar” é a mesma coisa que desenhar. Esclarecido esse termo, vamos achar o ponto de intersecção com o eixo $y$, zerando o $x$
$$f(x)=x^2$$
$$f(0)=0^2$$
$$f(0)=0$$
Agora zeraremos o $f(x)$ para achar onde o gráfico intersecta o eixo $x$
$f(x)=x^2$
$0=x^2$
Chegamos em uma equação de segundo grau incompleta, para resolvê-la, basta tirarmos a raiz quadrada de ambos os lados da equação, só que como precisaremos do delta, vamos resolver por Bháskara (não esqueça que os coeficientes $b$ e $c$ são iguais a zero)
$0=x^2$
$x^2=0$
$$a=1,b=0,c=0$$
$$x=\frac{-b\pm\sqrt{∆}}{2a}$$
$$x=\frac{-0\pm\sqrt{0^2-4.1.0}}{2.1}$$
$$x=\frac{-0\pm\sqrt{0}}{2}$$
$$x=\frac{-0\pm0}{2}$$
$$x_1=\frac{-0+0}{2}=0$$
$$x_2=\frac{-0-0}{2}=0$$
Temos duas raízes reais e iguais, e já que o coeficiente $a$ é positivo, a concavidade da parábola ficará voltada para cima. Agora vamos encontrar as coordenadas do vértice
X do vértice:
$$x_v=\frac{-b}{2a}=\frac{-0}{2.1}=\frac{-0}{2}=0$$
Y do vértice:
$$y_v=\frac{-∆}{4a}=\frac{-0}{4.1}=\frac{-0}{4}=0$$
O ponto de mínimo (vértice) vai coincidir com a origem do plano cartesiano, então teremos o seguinte gráfico:
2. Uma empresa que fabrica transformadores criou uma função que representa o lucro ganho em relação a quantidade de máquinas produzidas: $L(x)=-x^2+30x-200$. Qual o número máximo de transformadores que eles devem produzir para atingir o maior lucro? Obs: O lucro é na casa dos milhares e é em reais.
Temos uma função quadrática e se foi pedido o valor máximo, o que nos interessa é apenas o vértice. Só que temos que entender o que cada coordenada irá nos indiciar, o “X do vértice” será a quantidade máxima de máquinas a serem produzidas, e o “Y do vértice” será o lucro máximo que eles irão obter ao produzir essa quantidade de peças. Sabendo essas informações, vamos calcular o delta e depois utilizar as fórmulas aprendidas
$$∆=b^2-4ac=30^2-4.(-1).(-200)=900-800=100$$
X do vértice:
$$x_v=\frac{-b}{2a}=\frac{-30}{2.(-1)}=\frac{-30}{-2}=15$$
Y do vértice:
$$y_v=\frac{-∆}{4a}=\frac{-100}{4.(-1)}=\frac{-100}{-4}=25$$
Portanto, eles precisam fabricar $15$ transformadores para atingir o lucro máximo de $25$ mil reais.
Formado em Eletrotécnica pelo IFRN, além de ter cursos de Matemática Básica e Cálculo pela empresa Help Engenharia.
