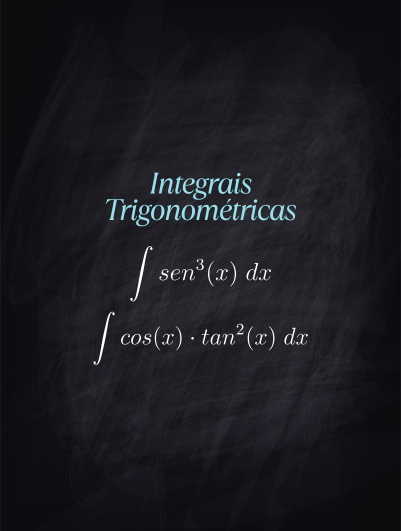Muitos alunos têm dificuldade com esse tipo de integral, não por se tratarem de integrais em si, mas por exigirem uma boa base em trigonometria. Neste artigo, explicarei o que são as integrais trigonométricas, como identificar e como resolver algumas delas.
O que é uma integral trigonométrica?
Seu nome é bem sugestivo, ele indica que esse tipo de integral, seja ele qual for, deve envolver apenas funções trigonométricas, como seno, cosseno e tangente, certo? Mais ou menos, as integrais trigonométricas são integrais de funções trigonométricas que estão elevadas a algum expoente maior que $n$ (com $n$ maior que $1$), podendo estar se multiplicando ou não, ou que não são podem ser resolvidas de forma direta, usando a tabela de integrais ou através do método da substituição, sendo necessária alguma manipulação matemática envolvendo relações trigonométricas.
Exemplos de integrais trigonométricas:
1) $\int sen^2(x)\;dx$
2) $\int cos^3(x)\cdot sen^2(x)\;dx$
3) $\int cos(x)\cdot sec(x)\;dx$
De forma geral, podemos dizer que as integrais trigonométricas se apresentam no formato:
$$\int\left[f(x)\right]^n\;dx\;\text{ou}\;\int\left[f(x)\right]^n\cdot\left[g(x)\right]^m\;dx$$
Onde $f(x)$ e $g(x)$ são funções trigonométricas quaisquer e $n$ e $m$ são expoentes maiores que $1$.
As integrais a seguir, não são consideradas integrais trigonométricas, pois apesar de envolverem apenas funções trigonométricas, é possível resolvê-las sem utilizar nenhuma relação da trigonometria.
1) $\int sen(x)+cos(x)\;dx$
2) $\int sen(2x)\;dx$
3) $\int \frac{cos(x)}{sen^2(x)}dx$
Como resolver uma integral trigonométrica?
Não há uma abordagem única que sirva para resolver todo e qualquer tipo de integral trigonométrica, devemos agir de acordo com a expressão que estivermos integrando, escolhendo a manipulação matemática adequada. Assim, para que consigamos resolver uma grande variedade de integrais trigonométricas, nosso conhecimento acerca da trigonometria e suas relações deve ser amplo. Nosso objetivo será simplificar ou reescrever a expressão, para que ela fique de um jeito que seja possível resolver utilizando a tabela ou algum método de integração (como a integração por substituição).
Exemplo 1: Calcule a integral a seguir
$$\int sen^3(x)\;dx$$
Não temos a integral de $sen^3(x)$ na tabela, nem é possível substituir seno por alguma letra, pois não conseguiremos achar quem é $dx$, portanto, é necessário manipular a expressão para conseguirmos integrar. Começarei transformando $sen^3(x)$ em $sen^2(x)\cdot sen(x)$ (caso tenha dúvida nesse processo, recomendo que leia o artigo sobre potenciação).
$$\int sen^3(x)\;dx=\int sen^2(x)\cdot sen(x)\;dx$$
Posso utilizar a relação fundamental da trigonometria (RFT) para transformar $sen^2(x)$ em $1-cos^2(x)$.
$$\int sen^2(x)\cdot sen(x)\;dx=\int\left(1-cos^2(x)\right)sen(x)\;dx$$
Do jeito que a expressão se encontra, é possível utilizar o método da substituição para resolvermos. Chamando $cos(x)$ de $u$, teremos:
$$u=cos(x)$$
$$\frac{du}{dx}=-sen(x)$$
$$-du=sen(x)\;dx$$
Substituindo na integral, ficaremos com:
$$\int (1-u^2)\;-du=-\int 1-u^2\;du$$
Então, resolvemos a integral acima utilizando a tabela
$$-\int 1-u^2\;du=-\left(u-\frac{u^3}{3}\right)+C=-u+\frac{u^3}{3}+C$$
Por fim, substituímos $u$ por $cos(x)$, pois nossa resposta deve estar em função da variável $x$.
$$-cos(x)+\frac{cos^3(x)}{3}+C$$
Exemplo 2: Calcule a integral a seguir
$$\int cos^3(x)\;dx$$
Novamente não é possível resolver a integral diretamente, então, vamos tentar fazer o mesmo que no exercício anterior, separando a potência de cosseno.
$$\int cos^3(x)\;dx=\int cos^2(x)\cdot cos(x)\;dx$$
Agora utilizamos a RFT no cosseno ao quadrado
$$\int cos^2(x)\cdot cos(x)\;dx=\int\left(1-sen^2(x)\right)cos(x)\;dx$$
Agora realizamos a substituição de $sen(x)$ por $u$ e resolvemos a integral resultante
$$u=sen(x)$$
$$du=cos(x)\;dx$$
$$\int\left(1-u^2\right)dx=u-\frac{u^3}{3}+C=sen(x)-\frac{sen^3(x)}{3}+C$$
Exemplo 3: Calcule a integral a seguir
$$\int sen^2(x)\;dx$$
Dessa vez o seno está elevado ao quadrado, e agora, o que fazer? Se transformarmos isso em seno vezes seno, não conseguiremos continuar o exercício, e se utilizarmos a RFT, teremos cosseno ao quadrado, que também é uma integral desconhecida até então. Utilizaremos a seguinte transformação trigonométrica para prosseguirmos com o cálculo:
$$sen^2(x)=\frac{1-cos(2x)}{2}$$
Fazendo isso transformamos $sen^2(x)$ quadrado em uma expressão trigonométrica elevada à $1$, que podemos resolver utilizando o método de integração por substituição.
$$\int \frac{1-cos(2x)}{2}\;dx=\frac{1}{2}\int \left(1-cos(2x)\right)\;dx$$
Nos resta agora resolver a integral
$$u=2x$$
$$du=2dx$$
$$\frac{du}{2}=dx$$
$$\frac{1}{2}\int \left(1-cos(u)\right)\;\frac{du}{2}=\frac{1}{2}\cdot\frac{1}{2}\int \left(1-cos(u)\right)\;du=$$
$$\frac{1}{4}\left(u-sen(u)\right)+C=\frac{1}{4}\left(2x-sen(2x)\right)+C$$
Exemplo 4: Calcule a integral a seguir
$$\int cos^2(x)\;dx$$
Da mesma forma que podemos deixar $sen^2(x)$ em uma função trigonométrica elevada à $1$, é possível fazer o mesmo para o cosseno ao quadrado:
$$cos^2(x)=\frac{1+cos(2x)}{2}$$
O processo a partir de agora será praticamente o mesmo da questão anterior, por esse motivo, irei resolver mais rapidamente, pois a parte da resolução que envolve trigonometria acaba por aqui.
$$\int cos^2(x)\;dx=\frac{1}{2}\int\left(1+cos(2x)\right)\;dx=\frac{1}{2}\left(x+\frac{sen(2x)}{2}\right)+C$$
Exemplo 5: Calcule a integral a seguir
$$\int sen^2(x)\cdot cos^3(x)\;dx$$
Temos o produto entre duas funções trigonométricas com expoentes maiores que $1$, então, precisaremos manipular a expressão para calcularmos a integral. E se separarmos o $cos^3(x)$ e usarmos a RFT assim como fizemos na integral do próprio $cos^3(x)$? Vamos testar e ver o que acontece.
$$\int sen^2(x)\cdot cos^2(x)\cdot cos(x)\;dx=\int sen^2(x)\left(1-sen^2(x)\right)\cdot cos(x)\;dx$$
Olha só, do jeito que está a integral, conseguimos utilizar o método da substituição.
$$u=sen(x)$$
$$du=cos(x)dx$$
$$\int u^2\left(1-u^2\right)\;du=\int\left(u^2-u^4\right)\;du$$
Caímos em uma integral muito simples, nos resta resolvê-la e substituir $u$ por $sen(x)$ no final
$$\int\left(u^2-u^4\right)\;du=\frac{u^3}{3}-\frac{u^5}{5}+C=\frac{sen^3(x)}{3}-\frac{sen^5(x)}{5}+C$$
Exemplo 6: Calcule a integral a seguir
$$\int sen^2(x)\cdot cos^2(x)\;dx$$
Dessa vez, temos o produto entre as funções seno e cosseno só que com expoentes pares, alguns dos leitores já devem imaginar o que farei. Mas para os que não perceberam, irei utilizar as transformações trigonométricas de seno e cosseno ao quadrado, as mesmas que foram usadas nos exemplos $3$ e $4$.
$$\int\left(\frac{1-cos(2x)}{2}\right)\cdot\left(\frac{1+cos(2x)}{2}\right)\;dx=\int\frac{1^2-cos^2(2x)}{4}\;dx=\frac{1}{4}\int\left(1-cos^2(2x)\right)\;dx$$
Podemos transformar $1-cos^2(2x)$ em $sen^2(2x)$
$$\frac{1}{4}\int sen^2(2x)\;dx$$
Pensa comigo, se tivéssemos $sen^2(x)$, poderíamos transformar em $\frac{1-cos(2x)}{2}$, após a transformação, note que o argumento do cosseno é o dobro do argumento do seno ao quadrado (o que era $x$, passou a ser $2x$), então, se fizermos o mesmo para $sen^2(2x)$, o resultado será $\frac{1-cos(4x)}{2}$, é exatamente isso que farei agora.
$$\frac{1}{4}\int\frac{1-cos(4x)}{2}\;dx=\frac{1}{8}\int\left(1-cos(4x)\right)\;dx$$
Finalmente acabaram as manipulações envolvendo a trigonometria, restando apenas uma simples integral por substituição para resolver.
$$\frac{1}{8}\int\left(1-cos(4x)\right)\;dx=\frac{1}{8}\left(x-\frac{sen(4x)}{4}\right)+C$$
Exemplo 7: Calcule a integral a seguir
$$\int cos(x)\cdot tan(x)\;dx$$
Para resolver essa questão, basta apenas saber a chamada “identidade trigonométrica”, que diz que a tangente é igual ao seno sobre o cosseno
$$\int cos(x)\cdot tan(x)\;dx=\int cos(x)\cdot\frac{sen(x)}{cos(x)}\;dx=\int sen(x)\;dx$$
Agora ficou fácil, chegamos em uma integral da tabela
$$\int sen(x)\;dx=cos(x)+C$$
Exemplo 8: Calcule a integral a seguir
$$\int sen(x)\cdot tan(x)\;dx$$
Vamos utilizar a identidade trigonométrica da tangente para tentar resolver
$$\int sen(x)\cdot tan(x)\;dx=$$
$$\int sen(x)\cdot\frac{sen(x)}{cos(x)}\;dx=$$
$$\int\frac{sen^2(x)}{cos(x)}\;dx$$
Mesmo que substituamos $sen(x)$ por $u$, o cosseno não está multiplicando o $dx$ para que consigamos o substituir, mas e se utilizarmos a RFT no $sen^2(x)$?
$$\int\frac{sen^2(x)}{cos(x)}\;dx=\int\frac{1-cos^2(x)}{cos(x)}\;dx$$
Podemos separar essa fração em duas frações com o mesmo denominador
$$\int\frac{1-cos^2(x)}{cos(x)}\;dx=\int\frac{1}{cos(x)}-\frac{cos^2(x)}{cos(x)}\;dx=\int\frac{1}{cos(x)}-cos(x)\;dx$$
O inverso do cosseno é a secante, então podemos reescrever a integral da seguinte forma:
$$\int\frac{1}{cos(x)}-cos(x)\;dx=\int sec(x)-cos(x)\;dx$$
Agora nos resta integrar as funções
$$\int sec(x)-cos(x)\;dx=\ln\left|sec(x)+tan(x)\right|-sen(x)+C$$
Exemplo 9: Calcule a integral a seguir
$$\int sec(x)\cdot sen(x)\;dx$$
A secante é o inverso do cosseno, então, comecemos reescrevendo a integral:
$$\int sec(x)\cdot cos(x)\;dx=\int\frac{1}{cos(x)}\cdot sen(x)\;dx=\int\frac{sen(x)}{cos(x)}\;dx$$
Caímos em uma integral por substituição tranquila de se resolver
$$u=cos(x)$$
$$-du=sen(x)dx$$
$$-\int\frac{1}{u}\;du=-\ln\left|u\right|+C=-\ln\left|cos(x)\right|+C$$
Exemplo 10: Calcule a integral a seguir
$$\int tan^2(x)\;dx$$
Como vimos no exercício anterior, para calcular a integral de $tan(x)$ transformamos tangente em seno sobre cosseno e utilizamos o método da substituição, mas e a integral de $tan^2(x)$? Podemos utilizar a segunda relação fundamental da trigonometria:
$$tan^2(x)=sec^2(x)-1$$
A primitiva (integral) de $sec^2(x)$ é $tan(x)$, então, conseguimos resolver utilizando a tabela.
$$\int tan^2(x)\;dx=\int\left(sec^2(x)-1\right)\;dx=tan(x)-x+C$$
Há uma infinidade de outros tipos de integrais trigonométricas, não sendo possível abordar todos neste artigo, no entanto, creio que os exercícios que resolvi já irão elucidar a mente de muitos, uma vez que a diferença deles para os demais, serão as manipulações matemáticas e as integrais resultantes após a simplificação.
Formado em Eletrotécnica pelo IFRN, além de ter cursos de Matemática Básica e Cálculo pela empresa Help Engenharia.
