Integrais impróprias: Aprenda a identificá-las e resolvê-las

Integrais
Teoria
13/05/2025
Daniel Duarte

A integral imprópria é, geralmente, o último tipo de integral a ser apresentado, e não é por acaso, dado que para resolvê-la pode ser necessário utilizar tudo o que foi aprendido em cálculo até então. No entanto, estou aqui para tentar mostrar que, por mais que seja trabalhosa, ela não é um monstro de $7$ cabeças.

O que é uma integral imprópria?

Basicamente, se trata de uma integral definida (que possui limites de integração), onde ao menos um dos limites de integração é infinito (ou menos infinito), ou um valor que não está está no domínio da função (que ao substituirmos na função que está sendo integrada, chegamos em uma indeterminação).

Exemplos de integrais impróprias:

1) $\int_{- \infty}^{2} \frac{1}{x} d x$

2) $\int_{- \infty}^{\infty} e^{x} d x$

3) $\int_{π}^{0} \frac{s e n (x)}{x} d x$

Podemos classificar a integral imprópria em três tipos, o primeiro é quando temos infinito ou menos infinito em pelo menos um dos limites de integração. O segundo é quando pelo menos um deles é um valor que não está no domínio da função, ou seja, que causaria uma indefinição ou indeterminação ao substituirmos na função. E o terceiro caso é a mistura dos anteriores.

Como resolver uma integral imprópria?

Começando pelo primeiro tipo de integral impríopria, identificamos qual limite de integração está tendendo a infinito, substituímos ele por uma letra qualquer, e calculamos o limite da integral, quando a letra tende a infinito. Antes de fazermos qualquer coisa, é interessante que calculemos a integral indefinida da função, pois mais cedo ou mais tarde, teremos que fazê-lo.

Exemplo 1: Calcule a integral definida abaixo

$\int_{- \infty}^{- 1} \frac{1}{x^{2}} d x$

Na questão acima, o limite inferior tende à $- \infty$ , portanto, se trata de uma integral imprópria. Comecemos calculando a integral indefinida.

$\int \frac{1}{x^{2}} d x = - \frac{1}{x} + C$

Agora, substituímos o limite inferior por uma letra e calculamos o limite da integral quando ela tende à $- \infty$ (utilizarei a letra $a$ , mas poderia ser qualquer letra que não seja $x$ )

$\int_{- \infty}^{- 1} \frac{1}{x^{2}} d x = lim_{a \to - \infty} \int_{a}^{- 1} \frac{1}{x^{2}} d x$

Como já sabemos o valor da integral, substituímos na expressão

$lim_{a \to - \infty} \int_{a}^{- 1} \frac{1}{x^{2}} d x = lim_{a \to - \infty} {- \frac{1}{x} |}_{a}^{- 1}$

Em seguida, substituímos os limites de integração

$lim_{a \to - \infty} {- \frac{1}{x} |}_{a}^{- 1} = lim_{a \to - \infty} - \frac{1}{(- 1)} - (- \frac{1}{(a)}) = lim_{a \to - \infty} 1 + \frac{1}{a}$

Por fim, resolvemos o limite para acharmos o resultado da integral imprópria

$lim_{a \to - \infty} 1 + \frac{1}{a} = 1 + \frac{1}{(- \infty)} = 1 + 0 = 1$

Quando o resultado é um valor finito, como $1$ , $10$ ou $- 7$ , dizemos que a integral é convergente, ou seja, seu valor converge (se aproxima) para um valor finito. Por mais que o intervalo de integração seja infinito, a área embaixo do gráfico vai ficando cada vez menor, e se somássemos todas as pequenas áreas, o resultado seria um valor muito próximo de $1$ .

Exemplo 2: Calcule a integral definida abaixo

$\int_{1}^{\infty} \frac{1}{x} d x$

Dessa vez, o limite superior é infinito, mas o processo será o mesmo, começando pelo cálculo da integral indefinida

$\int \frac{1}{x} d x = \ln | x | + C$

Na sequência, substituímos $\infty$ por $a$ e calculamos o limite da integral quando $a \to \infty$

$\int_{1}^{\infty} \frac{1}{x} d x = lim_{a \to \infty} \int_{1}^{a} \frac{1}{x} d x = lim_{a \to \infty} {\ln | x | |}_{1}^{a} =$

$lim_{a \to \infty} \ln | a | - \ln | 1 | = \ln | \infty | - \ln | 1 | = \infty - 0 = \infty$

Quando o valor tende a infinito ou menos infinito, dizemos que a integral é divergente, em outras palavras, a área abaixo do gráfico tende a um valor infinito. Entretanto, é possível que a integral seja considerada divergente em outra situação: Quando não conseguimos calcular seu resultado, mas uma parte dela tende a infinito ou menos infinito (vocês irão entender melhor quando chegarmos em uma questão que caia nesta situação).

Exemplo 3: Calcule a integral definida abaixo

$\int_{- \infty}^{\infty} e^{x} d x$

Os dois limites estão tendendo a infinito, o que fazer? Afinal, só conseguimos calcular o limite para uma letra só, então não é possível calcular? Utilizaremos uma propriedade de integral, que nos permite separar uma integral definida em duas integrais, a primeira vai do limite inferior até um valor intermediário e a segunda parte deste valor e termina no limite superior

$\int_{a}^{b} f (x) d x = \int_{a}^{c} f (x) d x + \int_{c}^{b} f (x) d x$

Nós que escolhemos o valor intermediário, só que para facilitar nossa vida, é interessante que o valor seja pequeno ou que ao substituirmos na expressão, resulte em cálculos simples. Irei escolher $0$ como valor intermediário, em breve você saberá o porquê. Calculemos então, a primitiva da função $e^{x}$

$\int e^{x} d x = e^{x} + C$

Em seguida, separamos a integral em duas, onde o novo limite superior da primeira será $0$ e o limite inferior da segunda será $0$

$\int_{- \infty}^{\infty} e^{x} d x = \int_{- \infty}^{0} e^{x} d x + \int_{0}^{\infty} e^{x} d x$

Agora, substituímos os limites de integração infinitos por letras e calculamos os limites das integrais para essas letras tendendo aos seus respectivos valores

$\int_{- \infty}^{0} e^{x} d x + \int_{0}^{\infty} e^{x} d x = lim_{a \to - \infty} \int_{a}^{0} e^{x} d x + lim_{b \to \infty} \int_{0}^{b} e^{x} d x$

A partir daqui o processo será o mesmo, substituímos o valor da integral, em seguida substituímos os limites de integração e por fim, calculamos os limites

$lim_{a \to - \infty} \int_{a}^{0} e^{x} d x + lim_{b \to \infty} \int_{0}^{b} e^{x} d x = lim_{a \to - \infty} {e^{x} |}_{a}^{0} + lim_{b \to \infty} {e^{x} |}_{0}^{b} =$

$lim_{a \to - \infty} e^{0} - e^{a} + lim_{b \to \infty} e^{b} - e^{0} = lim_{a \to - \infty} 1 - e^{a} + lim_{b \to \infty} e^{b} - 1 =$

$1 - e^{- \infty} + e^{\infty} - 1 = \frac{1}{e^{\infty}} + \infty = 0 + \infty = \infty$

A integral do exemplo $3$ é divergente.

Exemplo 4: Calcule a integral definida abaixo

$\int_{0}^{1} \frac{\ln | x |}{x} d x$

Não temos limites de integração infinitos, no entanto, o valor do limite inferior não está no domínio da função que está sendo integrada, e podemos averiguar isso ao tentarmos calcular $f (0)$

$f (x) = \frac{\ln | x |}{x}$

$f (0) = \frac{\ln | 0 |}{0}$

Não conseguimos calcular um valor para a função, logo, $x = 0$ não pertence ao domínio. Da mesma forma que fizemos na integral imprópria do tipo $1$ , substituiremos o limite de integração problemático, por uma letra e calcularemos o limite da integral, quando a letra tende a este valor, mas precisamos ter um cuidado especial, uma vez que se o número problemático estiver no limite de integração inferior, a letra tenderá a ele pela direita, e caso ele esteja no limite superior, a letra deve tender a ele pela esquerda. Vamos começar calculando a integral indefinida, utilizando a integração por substituição

$u = \ln | x |$

$d u = \frac{1}{x} d x$

$\int \frac{\ln | x |}{x} d x = \int u d u = \frac{u^{2}}{2} = \frac{{(\ln | x |)}^{2}}{2} + C$

Agora, realizamos o processo que fizemos anteriormente

$\int_{0}^{1} \frac{\ln | x |}{x} d x = lim_{a \to 0^{+}} \int_{a}^{1} \frac{\ln | x |}{x} d x = lim_{a \to 0^{+}} {\frac{{(\ln | x |)}^{2}}{2} |}_{a}^{1} =$

$lim_{a \to 0^{+}} \frac{{(\ln | 1 |)}^{2}}{2} - \frac{{(\ln | a |)}^{2}}{2} = lim_{a \to 0^{+}} 0 - \frac{{(\ln | a |)}^{2}}{2} = lim_{a \to 0^{+}} - \frac{{(\ln | a |)}^{2}}{2} =$

$- \frac{{(\ln | 0 |)}^{2}}{2}$

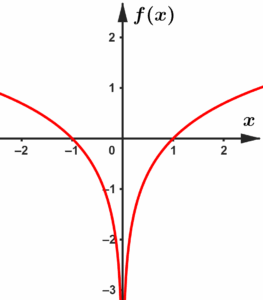
Acho importante interromper o cálculo aqui, pois não é tão óbvio saber o que acontece com o $\ln | x |$ quando $x$ tende à zero, para ajudar você a visualizar, vamos olhar o gráfico dessa função

Quando $x$ se aproxima de $0$ , o valor numérico da função $\ln | x |$ tende à $- \infty$ (tanto pela direita, quanto pela esquerda)

$- \frac{{(\ln | 0 |)}^{2}}{2} = - \frac{{(- \infty)}^{2}}{2} = - \frac{\infty}{2} = - \infty$

A função é divergente, para o intervalo de integração compreendido entre $x = 0$ e $x = 1$ .

Exemplo 5: Calcule a integral definida abaixo

$\int_{- 1}^{0} \frac{e^{x}}{e^{x} - 1} d x$

Assim como no exercício anterior, o valor, dentre os limites de integração, que não está no domínio da função é o $x = 0$ , pois $f (0)$ é uma indefinição matemática

$f (x) \frac{e^{x}}{e^{x} - 1}$

$f (0) \frac{e^{0}}{e^{0} - 1} = \frac{1}{1 - 1} = \frac{1}{0}$

Então, já sabemos quem chamar de $a$ , mas antes, calculemos a integral indefinida

$u = e^{x} - 1$

$d u = e^{x} d x$

$\int \frac{e^{x}}{e^{x} - 1} d x = \int \frac{1}{u} d u = \ln | u | = \ln | e^{x} - 1 | + C$

Por fim, repetimos o processo para finalizar o exercício

$\int_{- 1}^{0} \frac{e^{x}}{e^{x} - 1} d x = lim_{a \to 0^{-}} \int_{- 1}^{a} \frac{e^{x}}{e^{x} - 1} d x = lim_{a \to 0^{-}} {\ln | e^{x} - 1 | |}_{- 1}^{a} =$

$lim_{a \to 0^{-}} \ln | e^{a} - 1 | - \ln | e^{- 1} - 1 | = lim_{a \to 0^{-}} \ln | e^{a} - 1 | - \ln | \frac{1}{e} - 1 | =$

$\ln | e^{0} - 1 | - \ln | \frac{1}{e} - 1 | = \ln | 0 | - \ln | \frac{1}{e} - 1 | = - \infty - \ln | \frac{1}{e} - 1 | = - \infty$

Essa integral é divergente, entretanto, eu não precisava terminar o exercício para constatar isso, pois se ao menos um dos termos resultar em infinito ou menos infinito, a função como um todo irá divergir. Vale ressaltar, que a questão que estamos resolvendo, pede para calcular a integral, ela não pede para classificarmos em convergente ou divergente, então, é importante que você sempre preste atenção no enunciado, tanto para evitar cálculos desnecessários, como para não parar o cálculo antes da hora.

Exemplo 6: Calcule a integral definida abaixo

$\int_{\frac{π}{2}}^{\frac{3 π}{2}} c t g (x) d x$

Talvez seja difícil visualizar se essa integral é imprópria, pois a função é cotangente (temos aqui uma integral trigonométrica), e para muitos, o gráfico dela ou seus valores para diferentes ângulos, são desconhecidos. Para nos ajudar a analisar a questão, vamos transformar cotangente em cosseno sobre seno

$\int_{\frac{π}{2}}^{\frac{3 π}{2}} c t g (x) d x = \int_{\frac{π}{2}}^{\frac{3 π}{2}} \frac{c o s (x)}{s e n (x)} d x$

Se calcularmos $f (\frac{3 π}{2})$ e $f (\frac{π}{2})$ , não encontraremos nenhum problema

$f (x) = \frac{c o s (x)}{s e n (x)}$

$f (\frac{3 π}{2}) = \frac{c o s (\frac{3 π}{2})}{s e n (\frac{3 π}{2})} = \frac{0}{- 1} = 0$

$f (\frac{π}{2}) = \frac{c o s (\frac{π}{2})}{s e n (\frac{π}{2})} = \frac{0}{1} = 0$

Só que para o ângulo de $180 °$ , que equivale à $π$ radianos, há uma indefinição para a função cotangente

$f (π) = \frac{c o s (π)}{s e n (π)} = \frac{- 1}{0}$

Nessa situação, em que o valor problemático está entre os limites de integração, separamos a integral em duas, e o valor intermediário escolhido será justamente esse, que resulta na indefinição

$\int_{\frac{π}{2}}^{\frac{3 π}{2}} c t g (x) d x = \int_{\frac{π}{2}}^{π} c t g (x) d x + \int_{π}^{\frac{3 π}{2}} c t g (x) d x$

Então, substituímos o limite de integração por alguma letra e calculamos os limites, como já fizemos antes

$\int_{\frac{π}{2}}^{π} c t g (x) d x + \int_{π}^{\frac{3 π}{2}} c t g (x) d x = lim_{a \to π^{-}} \int_{\frac{π}{2}}^{a} c t g (x) d x + lim_{b \to π^{+}} \int_{b}^{\frac{3 π}{2}} c t g (x) d x$

Vamos ver se você está atento, falta calcular alguma coisa? Espero que sua resposta tenha sido “a integral indefinida”

$\int c t g (x) d x = \int \frac{c o s (x)}{s e n (x)} d x$

$u = s e n (x)$

$d u = c o s (x) d x$

$\int \frac{1}{u} d u = \ln | u | = \ln | s e n (x) | + C$

Por fim, terminamos de calcular a integral

$lim_{a \to π^{-}} \int_{\frac{π}{2}}^{a} c t g (x) d x + lim_{b \to π^{+}} \int_{b}^{\frac{3 π}{2}} c t g (x) d x = lim_{a \to π^{-}} {\ln | s e n (x) | |}_{\frac{π}{2}}^{a} + lim_{b \to π^{+}} {\ln | s e n (x) | |}_{b}^{\frac{3 π}{2}}$

$lim_{a \to π^{-}} \ln | s e n (a) | - \ln | s e n (\frac{π}{2}) | + lim_{b \to π^{+}} \ln | s e n (\frac{3 π}{2}) | - \ln | s e n (b) | =$

$lim_{a \to π^{-}} \ln | s e n (a) | - \ln | 1 | + lim_{b \to π^{+}} \ln | - 1 | - \ln | s e n (b) | =$

$lim_{a \to π^{-}} \ln | s e n (a) | - 0 + lim_{b \to π^{+}} 0 - \ln | s e n (b) | =$

$lim_{a \to π^{-}} \ln | s e n (a) | + lim_{b \to π^{+}} - \ln | s e n (b) | =$

$\ln | s e n (π) | - \ln | s e n (π) |$

Preciso parar a questão para te pedir que tenha muita cautela nesses cálculos envolvendo integrais impróprias, por mais que seja tentador sair cancelando os logaritmos e colocar na resposta que a integral converge para zero, a resposta estará errada. Vamos continuar calculando passo à passo e verificar

$\ln | s e n (π) | - \ln | s e n (π) | = \ln | 0 | - \ln | 0 | = - \infty - (- \infty) = \infty - \infty$

Chegamos em uma indeterminação, já que não há resposta para infinito menos infinito. Portanto, a integral é divergente, pois parte dela vai para infinito, mas não possui um valor numérico determinado.

Exemplo 7: Calcule a integral definida abaixo

$\int_{1}^{\infty} \frac{1}{{(x - 2)}^{2}} d x$

Agora, irei lhes apresentar ao tipo $3$ , o mais trabalhoso de integral imprópria, onde além de um dos limites de integração ser infinito (tipo $1$ ), um valor intermediário causa indeterminação (tipo $2$ )

$f (x) = \frac{1}{{(x - 2)}^{2}}$

$f (2) = \frac{1}{{(2 - 2)}^{2}} = \frac{1}{0}$

Antes de qualquer coisa, vamos calcular a integral indefinida

$u = x - 2$

$d u = d x$

$\frac{1}{u^{2}} d u = - \frac{1}{u} = - (\frac{1}{x - 2}) + C$

Os últimos dois exemplos deste artigo, terão resoluções extensas e cheias de detalhes, a chance de errar exercícios assim é muito alta, então, irei bem passo a passo. Comecemos separando a integral original em duas integrais, com a primeira indo de $1$ até $2$ e a outra indo de $2$ até $\infty$

$\int_{1}^{\infty} \frac{1}{{(x - 2)}^{2}} d x = \int_{1}^{2} \frac{1}{{(x - 2)}^{2}} d x + \int_{2}^{\infty} \frac{1}{{(x - 2)}^{2}} d x$

Se olharmos para a integral da direita, podemos notar que tanto o limite superior, quanto o inferior são problemáticos (uma situação parecida com a que encontramos no exemplo $3$ ), então, precisamos separar essa integral em duas, uma das integrais será calculada de $x = 2$ até $x = 3$ e a outra irá de $x = 3$ até $x = \infty$ (escolhi $3$ , pois facilitará os cálculos, mas eu poderia ter escolhido qualquer valor intermediário entre $2$ e $\infty$ )

$\int_{1}^{2} \frac{1}{{(x - 2)}^{2}} d x + \int_{2}^{\infty} \frac{1}{{(x - 2)}^{2}} d x = \int_{1}^{2} \frac{1}{{(x - 2)}^{2}} d x + [\int_{2}^{3} \frac{1}{{(x - 2)}^{2}} d x + \int_{3}^{\infty} \frac{1}{{(x - 2)}^{2}} d x]$

O próximo passo será substituir os limites de integração problemáticos por letras e calcular os limites das integrais para as letras tendendo aos seus respectivos valores

$\int_{1}^{2} \frac{1}{{(x - 2)}^{2}} d x + [\int_{2}^{3} \frac{1}{{(x - 2)}^{2}} d x + \int_{3}^{\infty} \frac{1}{{(x - 2)}^{2}} d x] =$

$lim_{a \to 2^{-}} \int_{1}^{a} \frac{1}{{(x - 2)}^{2}} d x + [lim_{b \to 2^{+}} \int_{b}^{3} \frac{1}{{(x - 2)}^{2}} d x + lim_{c \to \infty} \int_{3}^{c} \frac{1}{{(x - 2)}^{2}} d x]$

Substituímos então, o resultado da integral indefinida

$lim_{a \to 2^{-}} {- (\frac{1}{x - 2}) |}_{1}^{a} + [lim_{b \to 2^{+}} {- (\frac{1}{x - 2}) |}_{b}^{3} + lim_{c \to \infty} {- (\frac{1}{x - 2}) |}_{3}^{c}]$

Irei utilizar uma propriedade dos limites que me permite puxar para fora do limite uma constante que estiver multiplicando a função, pois esse sinal negativo pode nos atrapalhar futuramente

$- lim_{a \to 2^{-}} {\frac{1}{x - 2} |}_{1}^{a} + [- lim_{b \to 2^{+}} {\frac{1}{x - 2} |}_{b}^{3} - lim_{c \to \infty} {\frac{1}{x - 2} |}_{3}^{c}]$

$- lim_{a \to 2^{-}} {\frac{1}{x - 2} |}_{1}^{a} - [lim_{b \to 2^{+}} {\frac{1}{x - 2} |}_{b}^{3} + lim_{c \to \infty} {\frac{1}{x - 2} |}_{3}^{c}]$

Chegou a hora de substituir os limites de integração

$- lim_{a \to 2^{-}} \frac{1}{a - 2} - (\frac{1}{1 - 2}) - [lim_{b \to 2^{+}} \frac{1}{3 - 2} - (\frac{1}{b - 2}) + lim_{c \to \infty} \frac{1}{c - 2} - (\frac{1}{3 - 2})]$

$- lim_{a \to 2^{-}} \frac{1}{a - 2} + 1 - [lim_{b \to 2^{+}} 1 - (\frac{1}{b - 2}) + lim_{c \to \infty} \frac{1}{c - 2} - 1]$

Por fim, resolvemos os limites

$- (\frac{1}{2 - 2} + 1) - [1 - (\frac{1}{2 - 2}) + \frac{1}{\infty - 2} - 1]$

$- (- \infty + 1) - [1 - (\infty) + 0 - 1] = \infty - (- \infty) = \infty + \infty = \infty$

A integral é divergente e seu resultado é infinito positivo.

Exemplo 8: Calcule a integral definida abaixo

$\int_{- \infty}^{\infty} \frac{1}{x} d x$

Por fim, mas não menos importante, temos a situação em que ambos os limites de integração são infinitos e há um valor problemático entre eles

$f (x) = \frac{1}{x}$

$f (0) = \frac{1}{0}$

Comecemos então, calculando a integral indefinida, que nesse caso, é facílima

$\int \frac{1}{x} d x = \ln | x | + C$

Agora, separamos a integral de forma que o valor intermediário seja justamente o número problemático (pois dessa forma abordaremos as duas situações de uma vez só)

$\int_{- \infty}^{\infty} \frac{1}{x} d x = \int_{- \infty}^{0} \frac{1}{x} d x + \int_{0}^{\infty} \frac{1}{x} d x$

Nas duas integrais, os dois limites de integração são problemáticos, então, precisaremos separá-las em quatro integrais, e para isso, escolherei os valores intermediários $- 1$ e $1$ para serem os novos limites de integração (os escolhi porque lá na frente, conseguirei eliminar alguns termos facilmente, uma vez que $\ln \ln | x |$ tanto para $x = 1$ ou $x = - 1$ , resulta em zero)

$[\int_{- \infty}^{- 1} \frac{1}{x} d x + \int_{- 1}^{0} \frac{1}{x} d x] + [\int_{0}^{1} \frac{1}{x} d x + \int_{1}^{\infty} \frac{1}{x} d x]$

Como vocês já devem estar cansados de ver, irei substituir os valores problemáticos por letras e calcular os limites das integrais

$[lim_{a \to - \infty} \int_{a}^{- 1} \frac{1}{x} d x + lim_{b \to 0^{-}} \int_{- 1}^{b} \frac{1}{x} d x] + [lim_{c \to 0^{+}} \int_{c}^{1} \frac{1}{x} d x + lim_{d \to \infty} \int_{1}^{d} \frac{1}{x} d x]$

Na sequência, substituímos o resultado da integral indefinida

$[lim_{a \to - \infty} {\ln | x | |}_{a}^{- 1} + lim_{b \to 0^{-}} {\ln | x | |}_{- 1}^{b}] + [lim_{c \to 0^{+}} {\ln | x | |}_{c}^{1} + lim_{d \to \infty} {\ln | x | |}_{1}^{d}]$

Chegou a hora de substituirmos os limites de integração

$[lim_{a \to - \infty} \ln | - 1 | - \ln | a | + lim_{b \to 0^{-}} \ln | b | - \ln | - 1 |] + [lim_{c \to 0^{+}} \ln | 1 | - \ln | c | + lim_{d \to \infty} \ln | d | - \ln | 1 |]$

$[lim_{a \to - \infty} 0 - \ln | a | + lim_{b \to 0^{-}} \ln | b | - 0] + [lim_{c \to 0^{+}} 0 - \ln | c | + lim_{d \to \infty} \ln | d | - 0]$

$[lim_{a \to - \infty} - \ln | a | + lim_{b \to 0^{-}} \ln | b |] + [lim_{c \to 0^{+}} - \ln | c | + lim_{d \to \infty} \ln | d |]$

Para finalizarmos com chave de ouro, resolvemos os limites

$[- \ln | - \infty | + \ln | 0 |] + [- \ln | 0 | + \ln | \infty |]$

$[- \infty - \infty] + [\infty + \infty] = \infty - \infty$

Caso a questão pedisse para determinarmos se a integral é convergente ou divergente, poderíamos parar o cálculo um pouco antes, mas decidi ir até o fim, pois há professores muito rigorosos pelo mundo afora. Nossa oitava e última integral é divergente, e não possui valor numérico determinado.

Abordei uma boa variedade de exercícios, mas as possibilidades são infinitas, e o nível de dificuldade das questões pode variar muito, pois quanto mais difícil for a integral indefinida, mais extenso será o cálculo.

Teste da comparação

Existem funções que não possuem primitivas. O cálculo das integrais dessas funções é complexo e exige técnicas avançadas ou computadores. Porém, é possível ter uma noção do que acontece com a área embaixo do gráfico delas, utilizando o chamado “teste da comparação”, que utiliza as integrais impróprias para analisar uma função como essa, de forma indireta. Farei um artigo específico para esse teste, pois ele é bem específico e um pouco difícil de entender.

Daniel Duarte

Formado em Eletrotécnica pelo IFRN, além de ter cursos de Matemática Básica e Cálculo pela empresa Help Engenharia.

Sobre nós

O Matematiquês é um blog dedicado ao aprendizado de matemática, e nosso objetivo é tornar o ensino mais acessível e envolvente através de conteúdos de alta qualidade e gratuitos para alunos e professores em todo o Brasil. Buscamos simplificar conceitos complexos com uma abordagem clara e direta, priorizando transparência, diversidade, clareza, qualidade, inovação e compromisso social. Nosso blog oferece conteúdos fundamentados por especialistas, revisados com rigor e atualizados.

Categorias

Posts mais recentes

All Post
Curiosidades
Ensino Fundamental
Ensino Médio
Ensino Superior
Livros
Notícias

Back
Cinemática
Dinâmica
Conceitos básicos da física

Back
Conceitos básicos da matemática
Frações
Potenciação
Radiciação
Geometria plana
Logaritmo

Back
Funções
Equações
Conjuntos numéricos
Geometria espacial
Inequações
Módulo
Progressões matemáticas
Física
Trigonometria
Cinemática
Dinâmica
Conceitos básicos da física

Back
Limites
Derivadas
Integrais
Equações Diferenciais
Vetores e Geometria Analítica

Integrais impróprias: Aprenda a identificá-las e resolvê-las

O que é uma integral imprópria?

Como resolver uma integral imprópria?

Teste da comparação

Sobre nós

Categorias

Posts mais recentes

Integrais impróprias: Aprenda a identificá-las e resolvê-las

Curso gratuito de limites, derivadas e integral

Integrais por partes cíclicas: Como identificar e resolver

Tags

Matematiquês © 2024. Todos os direitos reservados.