Vetor: O que é, operações e aplicações

Ensino Médio, Vetores e Geometria Analítica
Teoria
17/06/2025
Daniel Duarte

Os vetores são elementos matemáticos fundamentais, sendo amplamente utilizados na matemática e na física. Neste artigo, abordaremos desde suas características básicas — como módulo, direção e sentido — até operações como a soma vetorial. Explorarei este curioso objeto de estudo pela ótica da geometria euclidiana e da geometria analítica, conectando a intuição geométrica com a linguagem algébrica. A ideia é apresentar o tema de forma didática, sem abrir mão do rigor conceitual, mas aprofundando suficientemente no assunto para que seja criado um bom entendimento a respeito do tema.

O que é um vetor?

Um vetor pode ser descrito como um segmento de reta orientado, ou seja, um pedaço finito (limitado) de uma reta, com origem e extremidade (começo e fim), mas que possui um sentido, indicado por uma seta em um de seus lados. Para nos referirmos a um vetor qualquer, utilizamos uma letra com uma seta em cima: $\vec{u}$ , ou escrevemos letras maiusculas dos pontos em que ele está compreendido, com a seta em cima.

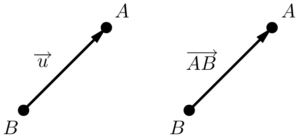
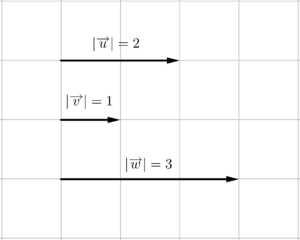
O vetor carrega três informações consigo: Módulo (comprimento, também chamada de magnitude), direção (vertical, horizontal, diagonal) e sentido (para cima, para a direita). Irei dedicar um tempinho para explicar cada uma delas, a fim de diminuir as possíveis dúvidas e confusões que são comuns a respeito delas. Representamos o módulo de um vetor com a notação dele dentro das barras verticais típicas do dispositivo matemático “módulo”, e isso não é por acaso, dado que não existe comprimento negativo, ele terá sempre valor positivo.

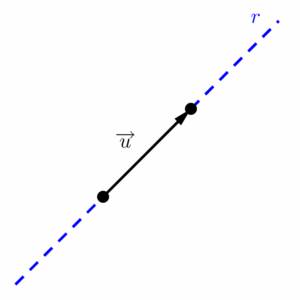
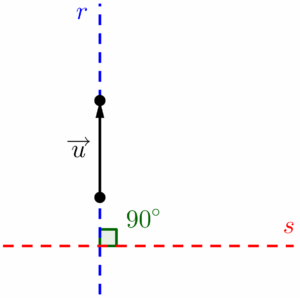
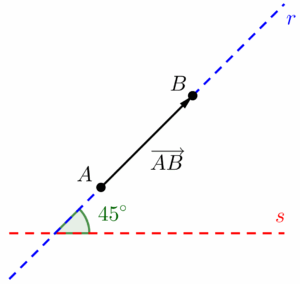
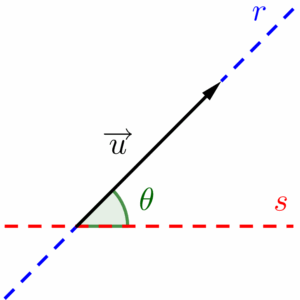
Para explicar o que é direção, preciso introduzir um conceito chamado “reta suporte”, que nada mais é do que o prolongamento do segmento orientado, representado por meio de uma linha tracejada. Noutras palavras, a reta suporte de um vetor (que chamarei de $r$ na imagem a seguir) é uma reta que contém o vetor (de um modo informal: seria a reta formada caso esticássemos o vetor infinitamente).

A direção de um vetor, pode ser entendida como o ângulo ou inclinação (apesar de não serem a mesma coisa, podem ser utilizados como sinônimos) da sua reta suporte em relação a uma outra reta horizontal qualquer.

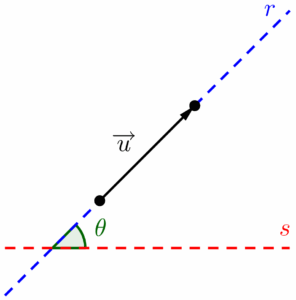
Se o ângulo formado entre elas for de noventa graus (ângulo reto), dizemos que o vetor está na direção vertical.

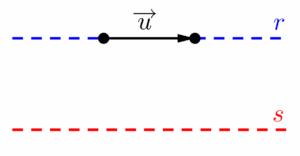
No caso do ângulo formado entre elas ser de zero graus, o vetor estará na direção horizontal, que acontecerá caso a reta suporte for paralela à reta horizontal (lembrando lá de geometria plana, duas retas são paralelas quando nunca se tocam, que por sua vez significa que elas possuem mesma inclinação).

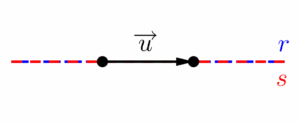
Ou se forem coincidentes, ou seja, estiverem por sobre a outra (A reta suporte toca a reta horizontal em todos os pontos).

E se o ângulo não for raso nem nulo, dizemos que o vetor está na direção diagonal ou que “forma tantos graus com a horizontal” (é mais comum escutarmos essa segunda menção na física). E por último, o sentido do vetor é indicado pela ponta da seta, e para enunciá-lo, utilizamos os pontos cardeais (Norte, sul, leste, oeste) ou palavras como “cima, baixo, direita e esquerda”. Desse modo, se um vetor está na direção horizontal e aponta para a direita, dizemos que o seu sentido é “da esquerda para a direita”.

Já se ele estiver na diagonal, nos será mais útil usar os pontos cardeais e colaterais. O vetor abaixo, por exemplo, está no sentido sudoeste – nordeste (partindo do sudoeste e indo em direção ao nordeste):

Alguns de vocês, possivelmente têm pouca familiaridade com a rosa dos ventos e os seus pontos, pensando nisso, deixo uma imagem de referência para que consigam entender o que quis dizer no parágrafo anterior.

Contextos de utilização do vetor

A necessidade da criação de um objeto matemático que tivesse não apenas a informação do valor numérico associado a ele, bem como direção e sentido, surgiu do estudo de grandezas (chamadas de grandezas vetoriais) que necessitavam de algo à mais que seu próprio valor numérico. Um dos exemplos é a velocidade, que não somente indica quanto que a posição de um corpo varia com o passar do tempo, mas também é utilizada para indicar para onde o corpo está se movendo, e como a vida como a conhecemos se dá em um espaço tridimensional (com três dimensões: comprimento, largura e profundidade), há uma exigência de indicar a direção e o sentido da velocidade, para termos uma ideia mais precisa de como o objeto está se movendo.

Representante de um vetor

Para que dois vetores quaisquer $\vec{u}$ e $\vec{v}$ sejam considerados iguais, eles precisam ter mesmo módulo, mesma direção e mesmo sentido, independentemente se as origens e extremidades deles são pontos diferentes.

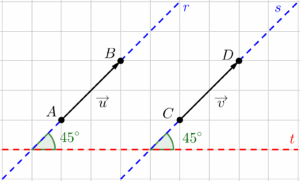
Visto que $\vec{u}$ e $\vec{v}$ são iguais, no exemplo acima, podemos dizer que o vetor $\vec{v}$ é um representante do vetor $\vec{u}$ (ou o contrário), o que significa que ambos são equivalentes: tanto faz utilizar um ou outro para representar determinada grandeza.

De modo geral, quaisquer vetores que forem iguais a um determinado vetor, serão considerados seus representantes. Assim, um vetor $\vec{u}$ genérico, possui infinitos representantes, pois há infinitas formas de representar um mesmo vetor, em diferentes posições, uma vez que o que importa para eles serem considerados iguais, é que tenham mesmo módulo, direção e sentido.

Tipos de vetores

Existem duas maneiras de classificar um vetor: de acordo com seu comprimento ou de acordo com a relação entre dois ou mais vetores.

Vetor unitário:

Chamamos um vetor $\vec{u}$ qualquer de “vetor unitário”, qualquer vetor que possui módulo igual à $1$ $(| \vec{u} | = 1)$ , independentemente de sua direção ou sentido.

Vetor nulo:

É um vetor que tem como origem e extremidade um único ponto, ou seja, possui comprimento igual à zero. É plausível então pensar que esse vetor nada mais é que um ponto, certo? Exatamente, um vetor nulo é representado como um ponto. Uma nomenclatura possível para um vetor nulo é o número zero com uma setinha em cima: $\vec{0}$

Vetores paralelos:

Dois vetores $\vec{u}$ e $\vec{v}$ são considerados paralelos por possuírem a mesma direção. Em outros termos: dois vetores são paralelos, quando suas retas suporte são paralelas entre si (formam o mesmo ângulo em relação à horizontal).

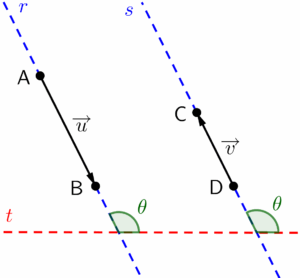
A notação que indica o paralelismo entre dois vetores é composta por duas barras verticais ou inclinadas uma do lado da outra.

$\vec{u} ∥ \vec{b}$

Vetores ortogonais:

São chamados de ortogonais ou perpendiculares, dois vetores $\vec{u}$ e $\vec{v}$ se formarem um ângulo de noventa graus um em relação ao outro, ou seja, suas retas suporte são perpendiculares (formam noventa graus entre si).

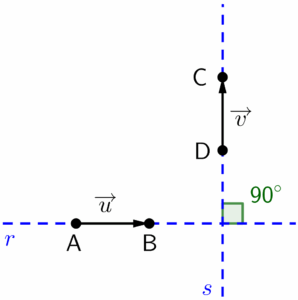
A notação que indica a ortogonalidade entre dois vetores é composta por barras perpendiculares.

$\vec{u} ⊥ \vec{b}$

Vetores opostos:

Quando dois vetores têm o mesmo comprimento, mesma direção, mas possuem sentidos contrários, eles são denominados “vetores opostos”. Se um determinado vetor $\vec{u}$ é oposto um vetor $\vec{v}$ , utilizamos a notação abaixo:

$\vec{u} = - \vec{w}$

Vetores iguais:

Como dito anteriormente, dois vetores são tidos como iguais se e somente se possuírem mesmo módulo, mesma direção e mesmo sentido.

Vetores coplanares:

São vetores que pertencem a um mesmo plano, ou seja, que estão numa mesma “dimensão espacial”. Ficou abstrato, não ficou? Geralmente no quotidiano, chamamos um objeto de plano, se ele possui uma superfície lisa, sem elevações ou depressões (parte afundada), então, uma folha de papel, uma tábua fina ou um lençol perfeitamente esticado são exemplos de figuras planas. Na matemática, um plano é como se fosse uma folha de papel infinita, mas que por limitações físicas, representamos por um retângulo bem delimitado.

Imagine que o chão de sua casa é o plano $α$ , representado na figura acima. Eis que você pega uma folha de papel e a recorta de modo que você obtenha algumas setas (analogia aos vetores), se você as colocar no chão, poderemos dizer que essas setas estão sobre uma mesma superfície plana. Trazendo para o matematiquês: vetores coplanares, estão sobre um mesmo plano.

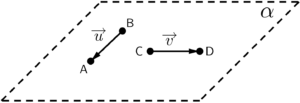
É válido mencionar que um plano não necessariamente precisa estar “deitado” (a parede é plana e está na vertical). Algumas considerações importantes para nosso entendimento a respeito dos vetores: dois vetores quaisquer, serão sempre coplanares entre si, em outras palavras, dados dois vetores $\vec{u}$ e $\vec{v}$ , podemos representá-los sem nenhuma dificuldade, estando sobre um mesmo plano. Entretanto, três vetores podem não ser coplanares, como podemos visualizar no exemplo abaixo:

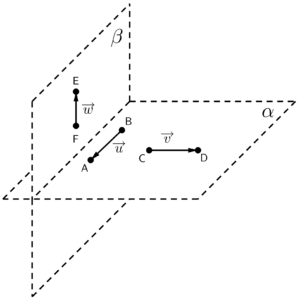
Para que você entenda melhor, voltemos à analogia. É como se pegássemos uma das setas que estavam no chão e a colássemos na parede. Nesse caso, ela deixaria de pertencer ao mesmo plano da figura.

Adição de vetores

Há três formas de somarmos vetores, a depender da relação entre eles. Se os vetores forem paralelos (possuírem mesma direção) e tiverem mesmo sentido, basta somarmos seus comprimentos, obtendo como resultado um vetor de mesma direção, mesmo sentido, e maior que os dois vetores que o originaram.

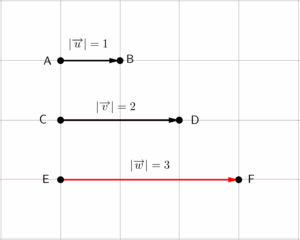
A representação algébrica da soma da figura acima pode ser feita de duas formas: tratando os vetores pelas letras que os identificam, ou pelas suas origens e extremidades.

$\vec{u} + \vec{v} = \vec{w}$

$\vec{A B} + \vec{C D} = \vec{E F}$

Se os vetores forem paralelos, mas tiverem sentidos opostos, iremos subtrair seus módulos, com o vetor resultante possuindo o mesmo sentido que o vetor de maior comprimento e a mesma direção de ambos.

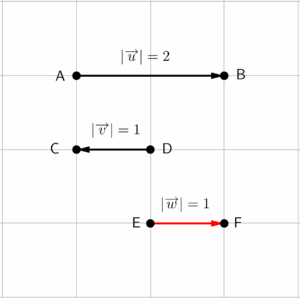
A representação algébrica da subtração vetorial acima será muito parecida com a anterior.

$\vec{u} - \vec{v} = \vec{w}$

$\vec{A B} + \vec{D C} = \vec{E F}$

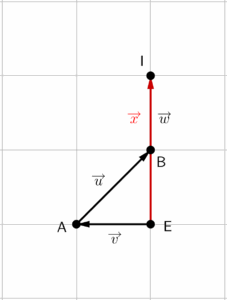
Agora, se os vetores que estão sendo somados não forem paralelos, utilizaremos o seguinte método para achar o vetor resultante: reposicionamos os vetores de modo que a origem seja a extremidade do outro, e em seguida, traçamos um vetor que parte da origem do primeiro vetor e termina na extremidade do último vetor que estiver sendo somado.

Exemplo: Dados dois vetores $\vec{u}$ e $\vec{v}$ , determine o vetor resultante da soma vetorial entre eles.

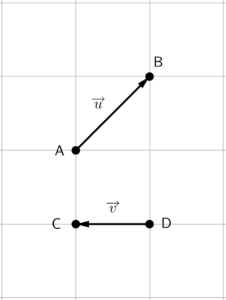
O primeiro passo é reposicionar o vetor $\vec{v}$ para que a extremidade dele coincida com a origem de $\vec{u}$ .

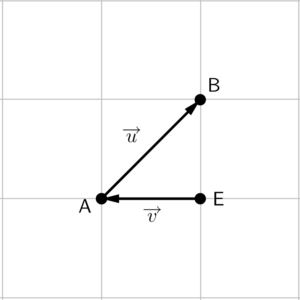
O vetor resultante, que chamarei de $\vec{w}$ , será o vetor que parte da origem do vetor $\vec{v}$ e termina na extremidade do vetor $\vec{u}$ .

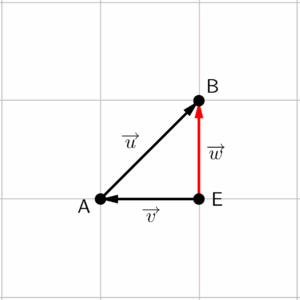
Note que seria possível reposicionar os vetores de uma outra forma, também respeitando a questão da origem e da extremidade coincidirem. Se for feito corretamente, o vetor resultante será o mesmo que encontramos na figura acima.

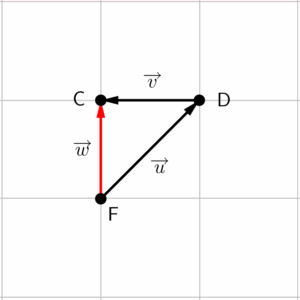
Para que fosse possível calcular o comprimento do vetor $\vec{w}$ , seria necessário que a questão desse os módulos dos outros dois vetores. Lembre-se que só é possível reposicionar um vetor, porque ele possui infinitos representantes, ou seja, qualquer vetor que tenha mesmo módulo, mesma direção e mesmo sentido que eles, serão seus representantes, portanto, podemos tratá-los como se fossem os “vetores originais” (diferentemente de uma reta, que a mudança de posição faz com que alteremos a reta).

Há uma segunda forma de somar esses mesmos vetores (ou quaisquer outros), que é pelo método do paralelogramo. Ele consiste no seguinte passo a passo: Reescrevemos os vetores de modo que a origem de ambos seja a mesma.

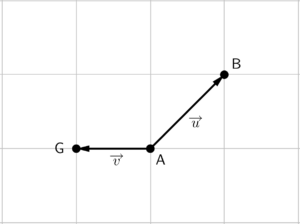
Desenhamos então um paralelogramo utilizando segmentos paralelos aos vetores $\vec{u}$ e $\vec{v}$ .

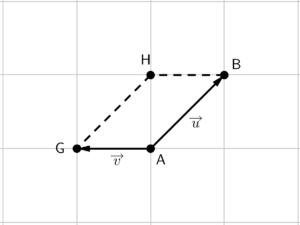
E por fim, o vetor resultante será o vetor que parte da origem em comum entre os vetores $\vec{u}$ e $\vec{v}$ (o ponto que é origem de ambos), e termina no vértice oposto (o ponto formado pelos segmentos que desenhamos para fechar o paralelogramo).

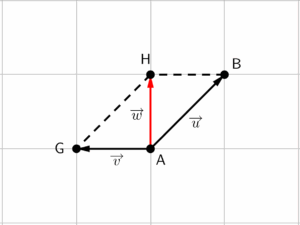
O método do paralelogramo é mais utilizado quando somamos dois vetores, para três ou mais, o método da origem e extremidade se torna bem mais prático, apesar de ambos chegarem num mesmo resultado. E para os curiosos de plantão, qual seria o vetor resultante da seguinte operação:

$\vec{u} + \vec{v} + \vec{w}$

Bom, como são três vetores, vamos utilizar o primeiro método de soma para vetores não paralelos.

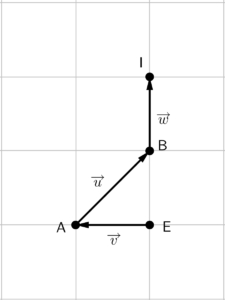
Nos resta ligar a origem do primeiro vetor ( $\vec{v}$ ) com a extremidade do último ( $\vec{w}$ ).

Propriedades da adição de vetores

É essencial conhecer as propriedades da soma ou subtração entre vetores, para facilitar os cálculos. A primeira é a propriedade comutativa: não importa a ordem em que somamos ou subtraímos vetores, o resultado será o mesmo.

$\vec{u} + \vec{v} + \vec{w} = \vec{w} + \vec{u} + \vec{v}$

A segunda é a propriedade associativa, utilizarei três vetores para exemplificar, mas funciona para qualquer quantidade. Dados três vetores $\vec{u}$ , $\vec{v}$ e $\vec{w}$ , tanto faz somar o $\vec{u}$ e $\vec{v}$ e somar o vetor resultante com $\vec{w}$ , ou somar $\vec{w}$ com $\vec{v}$ e depois somar com $\vec{u}$ .

$(\vec{u} + \vec{v}) + \vec{w} = \vec{u} + (\vec{v} + \vec{w})$

A terceira propriedade diz que ao somarmos um vetor $\vec{u}$ qualquer com o vetor nulo, obteremos como resultado o próprio vetor $\vec{u}$ .

$\vec{u} + \vec{0} = \vec{u}$

E a quarta propriedade consiste em: na soma de um vetor com seu oposto (vetor com mesmo módulo, mesma direção, mas sentido oposto), o resultado será um vetor nulo.

$\vec{u} + (- \vec{u}) = \vec{0}$

Essa última propriedade pode parecer confusa, mas o próximo tópico irá lhe ajudar a entendê-la.

Multiplicação de um vetor por um escalar

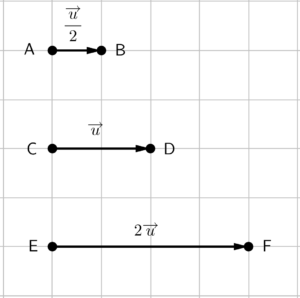
Multiplicar um vetor por uma constante (número escalar), poderá surtir dois efeitos: alterar o comprimento do vetor, seu sentido ou ambos. Se multiplicarmos um vetor $\vec{u}$ qualquer por $2$ , teremos como resultado um vetor de mesma direção, mesmo sentido e com o dobro do tamanho do vetor $\vec{u}$ . Já se multiplicarmos por meio, teremos um vetor com mesma direção, mesmo sentido e com metade do comprimento de $\vec{u}$ .

Caso o número que estiver multiplicando o vetor seja negativo, ele alterará também o sentido do vetor, além do seu comprimento. No entanto, se o número for igual a $- 1$ , apenas o sentido será alterado, mantendo-se o mesmo comprimento do vetor original. Então, dado um vetor $\vec{u}$ qualquer, o vetor $- \vec{u}$ será exatamente o vetor oposto à $\vec{u}$ , pois possuirá mesma direção, mesmo comprimento, mas sentido contrário à $\vec{u}$ . Agora é possível visualizar a quarta propriedade da soma vetorial: um vetor somado com seu oposto é igual ao vetor nulo.

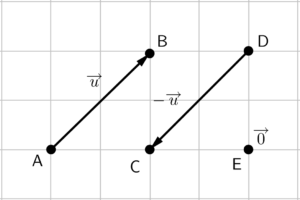
Se os vetores $\vec{u}$ e $- \vec{u}$ representassem o deslocamento de um corpo, o resultado dessa soma indicaria que o corpo se moveu de um ponto até outro, mas acabou voltando para o ponto de partida, ou seja, seu deslocamento efetivo foi zero.

Decomposição de um vetor

Existe um processo muito utilizado na física chamado “decomposição vetorial”, ele consiste na transformação de um vetor com direção diagonal, em dois outros vetores: um vertical e outro horizontal. Noutras palavras, é um processo de divisão de um vetor em duas componentes, que individualmente são mais simples do que o vetor original, facilitando o estudo de um fenômeno, movimento ou comportamento que é descrito por um vetor. Tomemos como exemplo um vetor $\vec{u}$ não nulo com uma determinada direção e sentido.

Suas componentes vertical ( ${\vec{u}}_{y}$ ) e horizontal ( ${\vec{u}}_{x}$ ), são vetores tais que a soma seja o próprio vetor $\vec{u}$ . Traduzindo do matematiquês: podemos reescrever o vetor $\vec{u}$ como sendo dois vetores, um que está na direção vertical e um na direção horizontal, mas eles devem ser vetores cuja soma resulta no vetor $\vec{u}$ .

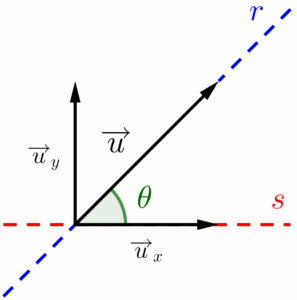
Alguns de vocês podem estar se perguntando:”Como descobriremos o comprimento das componentes?”, note que se deslocarmos o vetor ${\vec{u}}_{y}$ , conseguimos montar um triângulo retângulo com os três vetores.

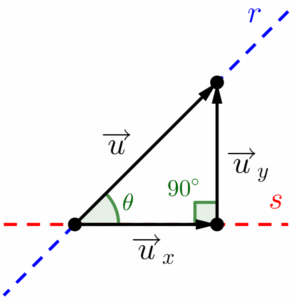
Levando em consideração que numa questão que exige uma decomposição vetorial, nos será dado o comprimento do vetor $\vec{u}$ e o seu ângulo em relação à horizontal (direção), conseguiremos através das razões trigonométricas seno e cosseno, encontrar os comprimentos de ${\vec{u}}_{y}$ e ${\vec{u}}_{x}$ .

$s e n (θ) = \frac{C a t e t o o p o s t o}{H i p o t e n u s a} = \frac{| {\vec{u}}_{y} |}{| \vec{u} |} ∴ | {\vec{u}}_{y} | = | \vec{u} | \cdot s e n (θ)$

$c o s (θ) = \frac{C a t e t o a d j a c e n t e}{H i p o t e n u s a} = \frac{| {\vec{u}}_{x} |}{| \vec{u} |} ∴ | {\vec{u}}_{x} | = | \vec{u} | \cdot c o s (θ)$

Eu sei, eu sei, provavelmente a linguagem está muito “matemática” e talvez não esteja tão clara a explicação para algumas pessoas, então, irei resolver um exercício para que fique esclarecido o processo de decomposição vetorial.

Exemplo: Dado um vetor $\vec{u}$ com módulo igual à $2$ , com ângulo de $\frac{π}{4}$ com a horizontal e sentido de sudoeste-nordeste, calcule o módulo das suas componentes vertical e horizontal.

Primeiramente, precisamos entender como é esse vetor. A questão nos deu um ângulo em radianos, é interessante que convertamos para graus, a fim de nos orientar na hora de representar o vetor $\vec{u}$ . Esse ângulo em radianos equivale à $45$ graus, e se a direção é sudoeste-nordeste, o vetor aponta para no sentido da esquerda para a direita e de baixo para cima (as componentes ajudam a visualizar isso).

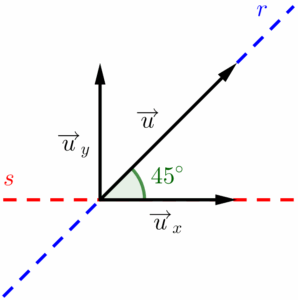
Para achar o módulo das componentes, basta utilizarmos as expressões que apresentei anteriormente.

$| {\vec{u}}_{y} | = | \vec{u} | \cdot s e n (θ) = 2 \cdot s e n (45 °) = 2 \cdot \frac{\sqrt{2}}{2} = \sqrt{2}$

$| {\vec{u}}_{c} | = | \vec{u} | \cdot c o s (θ) = 2 \cdot c o s (45 °) = 2 \cdot \frac{\sqrt{2}}{2} = \sqrt{2}$

Vetor no plano cartesiano

Até então estou tratando o vetor de acordo com a “geometria euclidiana”, que tem como foco os elementos geométricos e suas relações: ponto, reta, plano, paralelismo, perpendicularidade, etc. Porém, essa não é a única forma de analisar e trabalhar com vetores; com o avanço dos estudos de um matemático influente, chamado René Descartes, foi desenvolvido um sistema de coordenadas denominado “plano cartesiano”, onde cada ponto é representado como um par ordenado $(x, y)$ , que possui um valor referente ao eixo $x$ (eixo horizontal) e ao eixo $y$ (eixo vertical).

Esse sistema permitiu não somente determinar com precisão a posição de um ponto qualquer, como criar modelos estratégicos para subdividir regiões a partir de coordenadas (se você já jogou xadrez ou batalha naval, já terá se deparado com um sistema de coordenadas).

A partir da inserção dos elementos geométricos no plano cartesiano, foi possível analisá-los por uma perspectiva diferente, além de permitir representá-los algebricamente, facilitando o cálculo de alguns parâmetros e até o desenho de elementos mais complexos. A essa junção do sistema de coordenadas criado por Descartes com os elementos geométricos, foi dado o nome de “Geometria Analítica”, que será a área de estudo que iremos começar a adentrar neste momento.

Representação de um vetor através da sua origem e extremidade

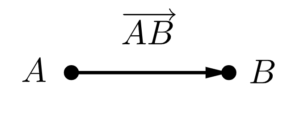
No contexto da geometria analítica, podemos representar um vetor de duas formas (não graficamente, pois ele continua sendo um segmento de reta orientado), a primeira é através dos pontos de origem e extremidade do vetor.

Exemplo: Dados os pontos $A (1, 1)$ e $B (3, 2)$ , represente no plano cartesiano os vetores $\vec{A B}$ e $\vec{B A}$ .

Primeiramente, começaremos representando os pontos que a questão deu no plano cartesiano.

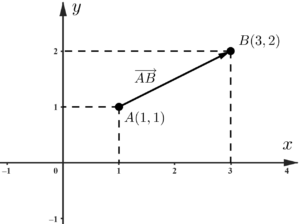
O vetor $\vec{A B}$ , tem origem no ponto $A$ e extremidade no ponto $B$ , ou seja, ele terá a mesma direção que o segmento $\overset{―}{A B}$ e o sentido será de $A$ para $B$ (apontando para o ponto $B$ ).

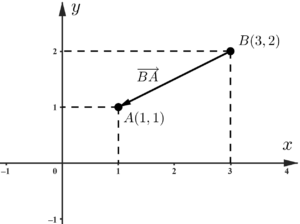
Já o vetor $\vec{B A}$ tem a mesmas direção e comprimento que o vetor $\vec{A B}$ , mas sentido contrário, pois ele aponta para o ponto $A$ (tem origem em $B$ e extremidade em $A$ ).

Antes de abordar a segunda forma de representar algebricamente um vetor, preciso explicar um conceito muito importante.

Bases canônicas

De forma simplificada, uma base canônica é um vetor unitário, que tem origem no ponto $(0, 0)$ e que detém a mesma direção que um dos eixos coordenados. Noutras palavras, são vetores com módulo igual à $1$ , sua origem coincide com a origem do plano cartesiano, e ele possui a mesma inclinação que os eixos $x$ e $y$ .

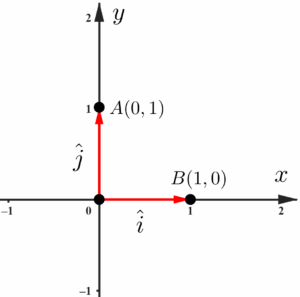
Acima temos as bases canônicas $\hat{i}$ e $\hat{j}$ , que possuem a mesma direção que o eixo $x$ e $y$ , respectivamente. Assim como qualquer outro vetor, é possível multiplicá-los por um número escalar, podendo alterar seus comprimentos e sentidos (mas nunca a direção). Por exemplo, multiplicando a base $\hat{i}$ por $2$ , teremos como resultado um vetor de mesma direção, mesmo sentido, mas comprimento igual à $2$ .

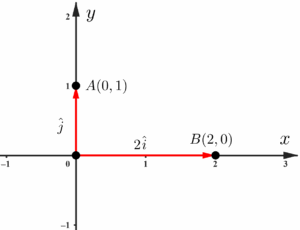
É indispensável mencionar que no momento em que multiplicamos uma base canônica por algum número, o vetor resultante não será chamado de base canônica, trataremos ele apenas como um vetor que é múltiplo da base em si.

Representação de um vetor em relação às bases canônicas

Uma vez entendido o conceito de base canônica e de seus múltiplos, abordarei o segundo tipo de representação vetorial na geometria analítica. Podemos escrever um vetor como o resultado da soma de vetores que são múltiplos das bases canônicas; resgatando o exemplo anterior, o vetor $\vec{u} = 2 \hat{i} + \hat{j}$ é o vetor resultante da soma dos vetores $2 \hat{i}$ e $\hat{j}$

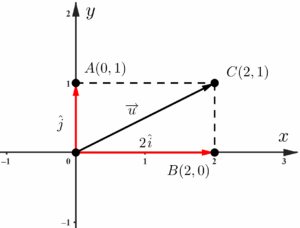
Você deve ter estranhado a falta da seta em cima das letras que indicam os vetores $2 \hat{i}$ e $\hat{j}$ . Essa ausência não se trata de um erro de notação, apenas é mais comum representarmos vetores que são múltiplos das bases canônicas (ou elas próprias) utilizando o “chapéu” (acento circunflexo) no lugar da seta, mas não seria errado, apesar de pouco usual, representar esses vetores como $2 \vec{i}$ e $\vec{j}$ .

Outra forma de representar esse mesmo vetor é com uma notação de par ordenado, onde a coordenada em $x$ é o comprimento do vetor $2 \hat{i}$ , e a coordenada em $y$ é o comprimento do vetor $\hat{j}$ (como uma base canônica possui comprimento igual à $1$ , ao multiplicarmos ela por $3$ , por exemplo, obteremos um vetor de módulo igual à $3$ , e assim por diante).

$\vec{u} = (2, 1)$

Os vetores que são representados de uma dessas duas formas (que relacionam-os com as bases canônicas), são vetores que partem sempre da origem do plano cartesiano. Em outras palavras, se uma questão te der um vetor assim:

$\vec{u} = a \hat{i} + b \hat{j}$

Com $a$ e $b$ sendo constantes quaisquer. Ou dessa outra forma:

$\vec{u} = (x, y)$

Significa que ela está considerando que o vetor tem origem no ponto $(0, 0)$ , então, quando você for representá-lo no plano cartesiano, deve-se considerar essa informação.

Vetor posição

Chamamos de “vetor posição” todo e qualquer vetor que parte da origem do plano cartesiano, ou seja, que tem origem no ponto $(0, 0)$ .

Módulo de um vetor no plano cartesiano

Para determinar o comprimento de um vetor no plano (para não ficar repetindo a palavra “cartesiano”, considere que toda vez que eu falar plano a partir de agora, estarei falando dele), basta calcularmos a raiz quadrada da soma das componentes $x$ e $y$ ao quadrado.

$| \vec{u} | = \sqrt{a^{2} + b^{2}}$

Exemplo: Calcule o módulo do vetor abaixo.

$\vec{u} = 3 \hat{i} - 4 \hat{j}$

Primeiramente, identificamos as componentes $x$ e $y$ , que nesse caso, são $3$ e $- 4$ , respectivamente (as constantes que multiplicam $\hat{i}$ e $\hat{j}$ ). Em seguida, utilizamos a expressão para o cálculo do módulo de um vetor.

$| \vec{u} | = \sqrt{a^{2} + b^{2}} = \sqrt{3^{2} + (- 4^{2})} = \sqrt{9 + 16} = \sqrt{25} = 5$

Mostrarei de onde vem a expressão acima, a partir de um vetor genérico. Tomemos um vetor $\vec{u} = a \hat{i} + b \hat{j}$ , com $a$ e $b$ sendo constantes quaisquer.

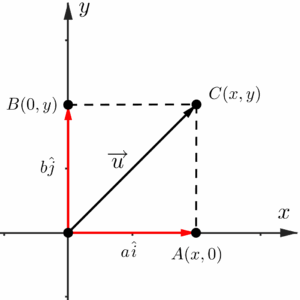
Podemos montar um triângulo retângulo associado a esse vetor, cujo cateto oposto mede $b$ , o cateto adjacente tem comprimento igual à $a$ e a hipotenusa é o próprio módulo do vetor $\vec{u}$ .

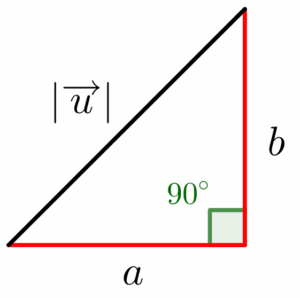
Utilizando o teorema de Pitágoras, conseguimos determinar a expressão para o cálculo do módulo de $\vec{u}$ .

$| \vec{u} |^{2} = a^{2} + b^{2}$

$| \vec{u} | = \sqrt{a^{2} + b^{2}}$

Há outra forma de calcular o módulo, caso queiras utilizar a notação de vetor relacionada a origem e extremidade dele, no entanto, para essa demonstração, é necessário o conhecimento de uma operação vetorial que não será abordada neste artigo, então, por enquanto, é melhor converter para a notação em relação às bases canônicas e utilizar a expressão acima.

Vetor no espaço

A evolução do plano cartesiano é o que chamamos de “espaço tridimensional cartesiano” ou “espaço cartesiano”, que consiste em adicionarmos um novo eixo, perpendicular à $x$ e $y$ , e obter assim um sistema de coordenadas que é capaz de localizar um determinado ponto em relação à três eixos, cuja representação algébrica das coordenadas é dada por um terno ordenado.

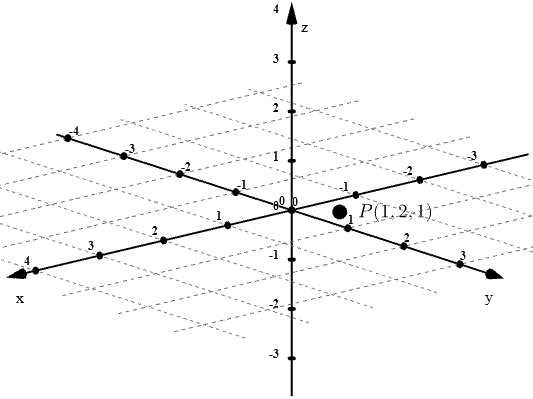
Pode ser útil traçar linhas de referência para conseguirmos ter uma melhor noção de onde exatamente está o ponto.

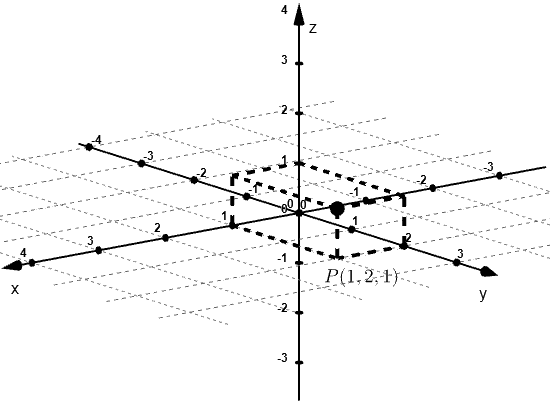
Trazendo isso para a vida real: para localizarmos um determinado objeto que está em cima de algum móvel, podemos utilizar como referência sua altura, e a distância dele em relação a duas paredes do cômodo. Se estivermos querendo desenhar um objeto do jeito que ele é fisicamente, precisaremos desenhá-lo de forma que consigamos distinguir sua largura, comprimento e altura (três dimensões, três eixos, conseguiu associar?).

Da mesma forma que conseguimos representar um ponto no espaço, é possível também representar um vetor. Se quisermos representá-lo em relação a sua origem e extremidade, basta marcarmos os pontos e desenhar um vetor ligando eles.

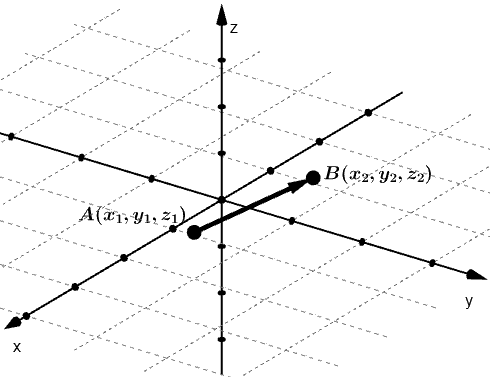
Soma vetorial no espaço

Para somar dois vetores quaisquer no espaço, utilizamos o método de colocar a origem de um coincidindo com a extremidade do outro (a regra do paralelogramo também serve, mas é necessário um conhecimento sobre planos para que seja entendível), e o vetor resultante será o vetor que parte da origem do primeiro vetor e termina na extremidade do último (vale ressaltar que tudo aquilo que você aprendeu a respeito de vetor para a geometria euclidiana, continua valendo para a geometria analítica).

Bases canônicas no espaço

No espaço cartesiano, surge mais uma base canônica (além das duas que vimos anteriormente), que chamamos de $\hat{k}$ , ela tem mesma direção e sentido que o eixo $z$ e possui módulo igual à $1$ , como as demais.

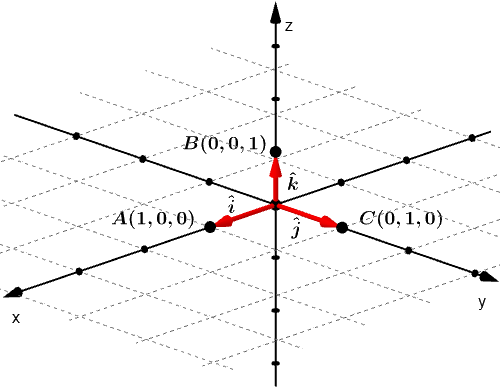
Representações algébricas de um vetor no espaço

As notações são as mesmas que o vetor no plano: podemos apresentar um vetor informando sua origem e extremidade ou representá-lo com uma expressão que o relaciona com as bases canônicas, com a diferença que o vetor poderá ter até três componentes (três coordenadas).

$\vec{u} = a \hat{i} + b \hat{j} + c \hat{k}$

$\vec{u} = (a, b, c)$

É importante mencionar que as coordenadas de um vetor são chamadas por nomes específicos, que remetem aos eixos coordenados. A componente $x$ é chamada de abscissa, a $y$ de ordenada e a $z$ de cota.

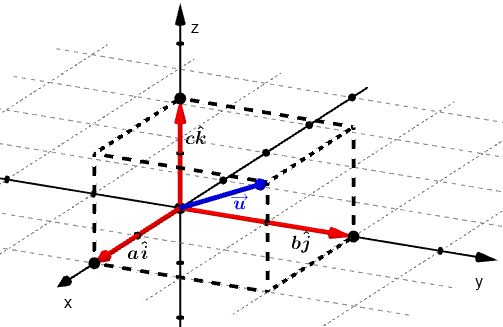
Como podemos ver na figura acima, para determinar um vetor com base em vetores que são múltiplos das bases canônicas, é interessante desenhar um paralelepípedo ligando os pontos, com o vetor resultante partindo do ponto $(0, 0, 0)$ e indo até o vértice na diagonal oposta.

Módulo de um vetor no espaço

De forma parecida com o vetor no plano, obteremos o módulo do vetor no espaço ao calcularmos a raiz quadrada das suas componentes ao quadrado.

$| \vec{u} | = \sqrt{a^{2} + b^{2} + c^{2}}$

Deixarei a demonstração dessa expressão para outro artigo, mas resolverei um exercício para que não fique muito abstrato e consiga visualizar ela funcionando na prática.

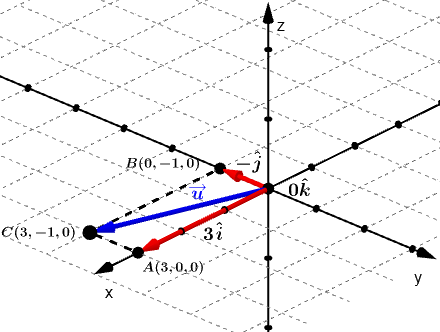
Exemplo: Calcule o módulo do vetor abaixo.

$\vec{u} = (3, - 1, 0)$

Utilizaremos a expressão vista agora a pouco para calcular o módulo.

$| \vec{u} | = \sqrt{a^{2} + b^{2} + c^{2}} = \sqrt{3^{2} + (- 1)^{2} + 0^{2}} = \sqrt{9 + 1} = \sqrt{10}$

Alguns de vocês devem estar se perguntando:”A coordenada em $z$ é zero, o que isso significa? Como representaríamos ele no espaço?”, a resposta para a primeira pergunta é que quando uma das componentes é zero, o vetor será representado no plano formado pelos demais eixos, no caso acima, o vetor estará no plano $x y$ , e sua representação no espaço seria assim:

Como somar vetores algebricamente

á vimos como somar vetores geometricamente, mas então, como somar dois vetores a partir de suas expressões algébricas? Basicamente, devemos somar (ou subtrair) as componentes correspondentes, ou seja, a componente $x$ de um vetor com a componente $x$ do outro, a $y$ com a $y$ e a $z$ com a $z$ , caso o vetor tenha a terceira componente.

Exemplo 1: Dados os vetores $\vec{u} = 2 \hat{i} + \hat{j} - 4 \hat{k}$ e $\vec{v} = \hat{i} + 3 \hat{j}$ , calcule um vetor $\vec{w}$ , tal que $\vec{w} = \vec{u} + \vec{v}$ .

Quando uma das componentes não estiver na expressão, significa que ela é igual à zero. Então, para achar o vetor $\vec{w}$ , basta somarmos as correspondentes.

$\vec{w} = \vec{u} + \vec{v}$

$\vec{w} = 2 \hat{i} + \hat{j} - 4 \hat{k} + \hat{i} + 3 \hat{j} + 0 \hat{k}$

$\vec{w} = (2 + 1) \hat{i} + (1 + 3) \hat{j} + (- 4 + 0) \hat{k} = 3 \hat{i} + 4 \hat{j} - 4 \hat{k}$

Exemplo 2: Dados os pontos $A (2, 1)$ , $B (- 1, 2)$ , calcule a soma entre os vetores $\vec{A B}$ e $\vec{u} = (- 3, 5)$

Dessa vez nos foi informado os pontos de origem e extremidade de um vetor, o que fazer? Precisamos converter para a notação em relação às bases canônicas para podermos somá-los. Para fazermos isso, basta subtrairmos o ponto final (extremidade), menos o ponto inicial (origem) do vetor $\vec{A B}$ , de forma idêntica ao que acontece quando somamos vetores, operacionamos as coordenadas correspondentes ( $x$ com $x$ e $y$ com $y$ ).

$\vec{A B} = B - A = (2, 1) - (- 1, 2) = (2 + 1, 1 - 2) = (3, - 1)$

Agora é só somarmos com $\vec{u}$ .

$\vec{A B} + \vec{u} = (3, - 1) + (- 3, 5) = (3 + (- 3), - 1 + 5) = (0, 4)$

Versor de um vetor

O versor de um vetor é um vetor unitário que possui mesma direção e sentido que o vetor original, esse conceito é muito utilizado em alguns contextos, quando não estamos preocupados com o módulo ou quando se quer achar um vetor paralelo a outro. Para achar o versor de um vetor, basta dividir todas suas componentes pelo seu módulo.

$\vec{v} = \frac{\vec{u}}{| \vec{u} |}$

Exemplo: Calcule o versor do vetor $\vec{a} = (3, - 1, 1)$ .

Primeiramente, calculamos o módulo de $\vec{a}$ .

$| \vec{a} | = \sqrt{a^{2} + b^{2} + c^{2}} = \sqrt{(3)^{2} + (- 1)^{2} + (1)^{2}} = \sqrt{9 + 1 + 1} = \sqrt{11}$

Por fim, dividimos as componentes de $\vec{a}$ pelo seu módulo para acharmos o versor (você pode identificar o versor com qualquer letra, estou utilizando $v$ por preferência, apenas).

$\vec{v} = \frac{\vec{a}}{| \vec{a} |} = \frac{(3, - 1, 1)}{\sqrt{11}} = (\frac{3}{\sqrt{11}}, \frac{- 1}{\sqrt{11}}, \frac{1}{\sqrt{11}})$

Igualdade de vetores (Algebricamente)

Algebricamente, dizemos que dois vetores são iguais, se todas as suas componentes correspondentes forem iguais, ou seja, a componente $x$ de um tem que ser igual à componente $x$ do outro, a $y$ também e a $z$ idem.

Exemplo: Encontre o valor de $x$ , sabendo que $\vec{a}$ e $\vec{b}$ são iguais.

$\vec{a} = (x + 1, 3, 1) \vec{b} = (0, x + 2, 1$

Para que eles sejam iguais, necessariamente suas componentes devem ser iguais.

$\vec{a} = \vec{b}$

$(x + 1, 3, 1) = (0, 3, 1)$

Igualando as componentes em relação ao eixo $x$ , teremos:

$x + 1 = 0$

$x = - 1$

Paralelismo entre vetores

Para saber se dois vetores são paralelos, basta dividir as componentes correspondentes, se o resultado de todas as divisões forem iguais, então os vetores são paralelos, com um único detalhe: se uma ou mais componentes de um dos vetores for zero, as componentes correspondentes do outro devem ser iguais a zero também, caso não sejam, eles não são paralelos.

Exemplo 1: Verifique se os vetores $\vec{a} = (4, 2, 0)$ e $\vec{b} = (2, 1, 0)$ são paralelos.

Vamos dividir as componentes que não são zero e verificar se obtemos uma mesma constante.

$\frac{x_{a}}{x_{b}} = \frac{4}{2} = 2$

$\frac{y_{a}}{y_{b}} = \frac{2}{1} = 2$

Eles são vetores paralelos.

Exemplo 2: Verifique se os vetores $\vec{u} = 4 \hat{i}$ e $\vec{v} = 3 \hat{i} + 2 \hat{j}$ são paralelos.

Como $\vec{u}$ tem a componente em $y$ igual à zero e $\vec{v}$ não tem, já dá para determinar que eles não são paralelos.

Produtos escalar, vetorial e misto

Há duas outras operações com vetores: Produto escalar e produto vetorial, a primeira tem como resultado um número escalar, já a segunda resulta em um vetor ortogonal aos vetores que foi efetuado o produto vetorial, mas esses assuntos por si só abarcam muita teoria, tendo em vista o quão longo ficou este artigo, deixarei esses assuntos para artigos próprio. (O produto misto seria a mistura dessas duas operações).

Equações com vetores

Como o próprio nome sugere, é denominada “equação vetorial”, uma equação que possui vetores como variáveis, ou seja, o seu objetivo é encontrar um vetor, dada uma expressão matemática que o relaciona com outros vetores.

Exemplos de equações vetoriais:

1) $2 \vec{u} + 3 \vec{v} = \vec{w}$

2) $3 \vec{x} = 2 \vec{y}$

3) $\vec{a} - \vec{b} = \frac{\vec{c}}{3}$

Daniel Duarte

Formado em Eletrotécnica pelo IFRN.

Sobre nós

O Matematiquês é um blog dedicado ao aprendizado de matemática, e nosso objetivo é tornar o ensino mais acessível e envolvente através de conteúdos de alta qualidade e gratuitos para alunos e professores em todo o Brasil. Buscamos simplificar conceitos complexos com uma abordagem clara e direta, priorizando transparência, diversidade, clareza, qualidade, inovação e compromisso social. Nosso blog oferece conteúdos fundamentados por especialistas, revisados com rigor e atualizados.

Categorias

Posts mais recentes

All Post
Curiosidades
Ensino Fundamental
Ensino Médio
Ensino Superior
Livros
Notícias

Back
Cinemática
Dinâmica
Conceitos básicos da física

Back
Conceitos básicos da matemática
Frações
Potenciação
Radiciação
Geometria plana
Logaritmo

Back
Funções
Equações
Conjuntos numéricos
Geometria espacial
Inequações
Módulo
Progressões matemáticas
Física
Trigonometria
Cinemática
Dinâmica
Conceitos básicos da física

Back
Limites
Derivadas
Integrais
Equações Diferenciais
Vetores e Geometria Analítica

Vetor: O que é, operações e aplicações

O que é um vetor?

Contextos de utilização do vetor

Representante de um vetor

Tipos de vetores

Vetor unitário:

Vetor nulo:

Vetores paralelos:

Vetores ortogonais:

Vetores opostos:

Vetores iguais:

Vetores coplanares:

Adição de vetores

Propriedades da adição de vetores

Multiplicação de um vetor por um escalar

Decomposição de um vetor

Vetor no plano cartesiano

Representação de um vetor através da sua origem e extremidade

Bases canônicas

Representação de um vetor em relação às bases canônicas

Vetor posição

Módulo de um vetor no plano cartesiano

Vetor no espaço

Soma vetorial no espaço

Bases canônicas no espaço

Representações algébricas de um vetor no espaço

Módulo de um vetor no espaço

Como somar vetores algebricamente

Versor de um vetor

Igualdade de vetores (Algebricamente)

Paralelismo entre vetores

Produtos escalar, vetorial e misto

Equações com vetores

Sobre nós

Categorias

Posts mais recentes

Vetor: O que é, operações e aplicações

Determinante de uma matriz

Matrizes: O que são, operações e classificações

Tags

Matematiquês © 2024. Todos os direitos reservados.