Apesar das semelhanças com a equação, até no modo de resolver, a inequação é um conceito único e muito presente em determinados conteúdos como análise de domínio de funções, e ao determinarmos condições de existência para um determinado tipo de equação.
O que é uma inequação?
É uma sentença (ou expressão) matemática que possui como característica principal uma desigualdade, símbolo matemático que indica determinada condição que um termo possui ou deve possuir em relação a outro. São cinco os tipos de desigualdades, sendo elas:
$>$ (Maior)
$<$ (menor)
$\geq$ (maior ou igual)
$\leq$ (menor ou igual)
$\neq$ (diferente)
Para uma expressão ser considerada uma inequação, além de ter uma desigualdade, é necessária a presença de pelo menos uma variável (letra), caso não tenha, a expressão é considerada uma “desigualdade” apenas.
Exemplos de inequações:
1) $x-2\neq5x$
2) $x\geq20$
3) $4x^2-x<2$
Significado das desigualdades:
Cada um dos símbolos possui um significado específico, sendo essencial saber diferenciar cada caso, para não errares uma questão por um detalhe.
Maior:
O símbolo ($>$) indica que um valor é maior que outro
Exemplo:
$5>2$
Quem fica do lado das perninhas do “v deitado” é o maior valor e quem fica para onde o símbolo “aponta” é o menor. A desigualdade acima é verdadeira, pois $5$ é maior que $2$.
Menor:
O símbolo ($<$) indica que um valor é maior que outro
Exemplo:
$-2<3$
A lógica é a mesma que o símbolo anterior, o que estiver do lado que o símbolo aponta (nesse caso é o $-2$) é o menor valor e o outro é o menor. A desigualdade acima pode ser lida como “$-2$ menor que $3$ ou $3$ maior que $-2$”.
Maior ou igual:
O símbolo ($\geq$) indica que um valor deve maior ou igual a outro.
Exemplo:
1) $6\geq6$
2) $40\geq3$
Apesar de parecer a mesma coisa que o símbolo “maior”, há uma sutil diferença, os valores podem ser iguais e ainda sim a sentença será verdadeira. E não há como um valor ser igual e ao mesmo tempo ser maior que outro, são condições excludentes, e isso é ilustrado pelo conectivo “ou”.
Menor ou igual:
Muito parecido com o símbolo anterior, ($\leq$) indica que um valor deve menor ou igual a outro.
Exemplo:
1) $1\leq1$
2) $-1\leq0$
Como você já deve ter percebido, a diferença entre “maior” e “menor”, que é a mesma diferença entre “maior ou igual” e “menor ou igual”, é somente a forma em que interpretamos a desigualdade. Tomemos a desigualdade $-1\leq0$, tanto faz dizer que $-1$ é menor ou igual à $0$, quanto dizer o contrário, que $0$ é maior ou igual à $1$, ambas as formas estão corretas.
Diferente:
Seu nome é bem sugestivo, essa desigualdade ($\neq$) representa que dois valores são (ou devem ser) diferentes.
Exemplo:
$3\neq4$
Tipos de inequação
Há tantos tipos de inequação, quanto há de equações, no entanto, a maioria de exercícios abordam dois principais, que são as inequações de primeiro e segundo grau.
Inequação de 1° grau:
É o tipo mais simples, ela consiste em uma desigualdade que possui em ao menos um dos lados, uma incógnita de grau $1$.
Exemplo:
$3x-1>2$
A forma geral da inequação de $1°$ grau é:
$$ax+b\neq c$$
Sendo $a$, $b$ e $c$ números quaisquer e o símbolo pode ser um dos cinco tipos de desigualdade.
Inequação de 2° grau:
É uma inequação que possui pelo menos uma variável de grau $2$.
Exemplo:
$2x^2-4x-1\neq5$
A forma geral da inequação de $2°$ grau é:
$$ax^2+bx+c\neq0$$
Sendo $a$, $b$ e $c$ números quaisquer, com $a\neq0$. E sim, organizamos ela da mesma forma que uma equação de segundo grau e não é à toa, como descobriremos a seguir.
Como resolver uma inequação?
Ao resolvermos uma inequação, descobrimos um conjunto de soluções, ou seja, quais são os valores que a variável pode assumir para que a desigualdade continue sendo verdadeira. E para fazermos isso, precisamos isolar a variável deu um lado da inequação, deixando os valores numéricos do outro, praticamente da mesma forma que em uma equação, mas teremos que tomar certo cuidado, pois há uma especificidade que deve ser levada em conta.
Quando passamos um número negativo que está multiplicando ou dividindo, para o outro lado da inequação, precisamos inverter o símbolo de desigualdade (exceto o símbolo de diferente, ele permanece intacto), se não o fizermos, a desigualdade estará errada (isso serve para desigualdades comuns).
Exemplo:
$$10>-10$$
A sentença acima está correta, mas vamos manipulá-la para vermos o que acontece. Primeiramente, irei fatorar o $-10$ em $-5$ vezes $2$
$$10>-5.2$$
Agora irei passar o $2$, que é positivo, para o outro lado só que dividindo
$$10>-5.2$$
$$\frac{10}{2}>-5$$
$$5>-5$$
A desigualdade permaneceu verdadeira, pois $5$ é maior que $-5$, mas se ao invés de passar o $2$, eu tivesse passado o $-5$ para o outro lado?
$$10>-5.2$$
$$\frac{10}{-5}>2$$
$$-2>2$$
A sentença se tornou falsa, pois um número positivo sempre é maior que um número negativo, portanto, precisamos inverter o símbolo.
$$-2<2$$
Está tudo correto agora, vamos então, para as inequações.
Como resolver uma inequação de 1° grau?
A melhor forma de explicar é resolvendo uma questão, mas esse passo a passo servirá para todas de mesmo grau.
Exemplo:
Resolva a inequação abaixo
$$2x-3\neq5$$
Para inequações de primeiro grau, começamos a resolvê-la isolando a variável, assim como em uma equação de $1°$ grau
$$2x-3\neq5$$
$$2x\neq5+3$$
$$2x\neq8$$
$$x\neq\frac{8}{2}$$
$$x\neq4$$
Nossa solução é $4$, certo? Errado, achamos o valor que o $x$ não pode assumir, se ele for igual à $4$, nossa desigualdade não estará correta, irei mostrar substituindo o $4$ na expressão original
$$2x-3\neq5$$
$$2.4-3\neq5$$
$$8-3\neq5$$
$$5\neq5$$
Cinco não é diferente de $5$, portanto, chegamos em uma indeterminação, em outras palavras, $x=5$ não pertence ao conjunto de soluções para a inequação $2x-3\neq5$. Levando em consideração que a maioria dos exercícios, até o ensino médio, são resolvidos utilizando o conjunto dos números reais, irei fazer o mesmo aqui para escrever a resposta da inequação
$$S:{x\,\epsilon\,\mathbb{R} /x\neq4}$$
Essa resposta pode ser lida como “$x$ pertence aos reais, tal que $x$ seja diferente de $4$”, em outras palavras, as respostas são todos os valores do conjunto dos números reais, exceto o $4$.
Exemplo 2:
Resolva a inequação abaixo
$$4x-12>6x$$
Isolamos a variável
$$4x-12>6x$$
$$4x-6x>12$$
$$-2x>12$$
Iremos passar um número negativo que está multiplicando o $x$ para o outro lado dividindo, portanto, precisamos inverter a inequação ao fazermos isso
$$-2x>12$$
$$x<\frac{12}{-2}$$
$$x<6$$
Todos os valores de $x$ menores que $6$ são soluções possíveis para essa inequação. De outra forma:
$$S:{x\,\epsilon\,\mathbb{R}/x<6}$$
Como resolver uma inequação de 2° grau?
Já as inequações de segundo grau, são um pouco mais complicadas de se obter um resultado, pois além de isolarmos a variável, precisamos analisar para qual (ou quais) intervalo de $x$ nossa desigualdade será satisfeita (se o símbolo for de diferente, será mais fácil a análise).
Primeiramente, deixamos a inequação em sua forma padrão ($ax^2+bx+c\neq0$), depois resolvemos uma equação idêntica a ela, encontrando suas raízes, e por fim, estudamos o gráfico da função correspondente a equação, para visualizarmos os resultados da expressão para diferentes valores de $x$. Os possíveis gráficos que iremos encontrar são:
1° caso: Duas raízes reais e distintas, e parábola com concavidade para cima
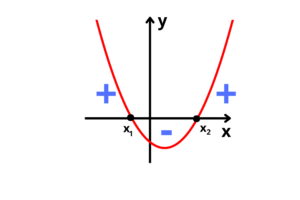
2° caso: Duas raízes reais e distintas, e parábola com concavidade para baixo
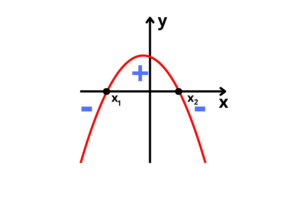
3° caso: Duas raízes reais e iguais, e parábola com concavidade para cima
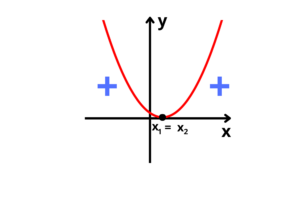
4° caso: Duas raízes reais e iguais, e parábola com concavidade para baixo
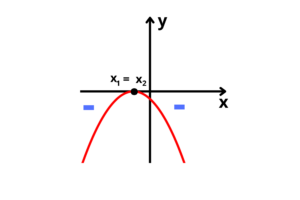
5° caso: Nenhuma raiz real e parábola com concavidade para cima
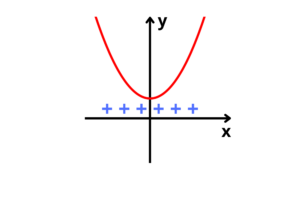
6° caso: Nenhuma raiz real e parábola com concavidade para baixo
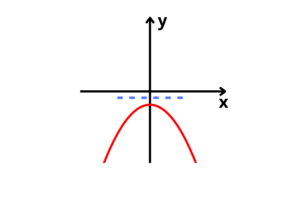
Todas as questões estarão organizadas na forma padrão, para facilitar os cálculos.
Exemplo 1:
Resolva a inequação abaixo
$$x^2-25\neq0$$
Como temos um símbolo de “diferente”, podemos resolver como se fosse uma equação, através da fórmula de Bháskara. Nesse caso em específico, como não há o termo que possui $x$, podemos resolver isolando a variável e aplicando a raiz quadrada em ambos os lados da inequação
$$x^2-25\neq0$$
$$x^2\neq25$$
$$\sqrt{x^2}\neq\sqrt{25}$$
$$x\neq\pm5$$
Portanto, todos os números reais, exceto $-5$ e $5$, são soluções para essa inequação
$$S:{x\,\epsilon\,\mathbb{R}/x\neq-5\,e\,x\neq5}$$
Exemplo 2:
Resolva a inequação abaixo
$$x^2+3x+2\geq0$$
Primeiramente, montamos uma equação idêntica a inequação (trocando somente a desigualdade pela igualdade), e então a resolvemos por Bháskara
$$x^2+3x+2=0$$
$$a=1, b=3, c=2$$
$$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$$
$$x=\frac{-3\pm\sqrt{3^2-4.1.2}}{2.1}$$
$$x=\frac{-3\pm\sqrt{1}}{2}$$
$$x=\frac{-3\pm1}{2}$$
$$x_1=\frac{-3+1}{2}=\frac{-2}{2}=-1$$
$$x_2=\frac{-3-1}{2}=\frac{-4}{2}=-2$$
Temos duas raízes reais e distintas, e pelo coeficiente $a$ ser positivo, temos uma concavidade para cima. Agora montamos o gráfico de uma função correspondente ($f(x)=x^2+3x+2$)
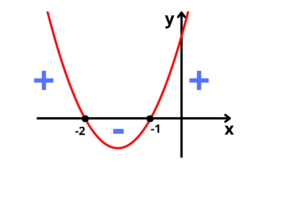
Para tornarmos a desigualdade verdadeira, precisamos dos valores de $x$ que ao substituirmos na expressão, resulte em valores maiores ou iguais à zero. As raízes são justamente os valores que fazem a inequação resultar em zero, portanto, elas são soluções válidas. Valores maiores que $-1$ ou menores que $-2$, fazem a função ficar positiva (como podemos ver no gráfico acima), então eles são soluções da inequação
$$S:{x\,\epsilon\,\mathbb{R}/x\leq-2\,ou\,x\geq1}$$
Exemplo 3:
Resolva a inequação abaixo
$$-x^2+5x-6>0$$
Montarmos uma equação equivalente e a resolvemos
$$-x^2+5x-6=0$$
$$a=-1, b=5, c=-6$$
$$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$$
$$x=\frac{-5\pm\sqrt{5^2-4.(-1).(-6)}}{2.(-1)}$$
$$x=\frac{-5\pm\sqrt{1}}{-2}$$
$$x=\frac{-5\pm1}{-2}$$
$$x_1=\frac{-5+1}{-2}=\frac{-4}{-2}=2$$
$$x_2=\frac{-5-1}{-2}=\frac{-6}{-2}=3$$
Duas raízes reais e distintas, e o gráfico terá concavidade para baixo
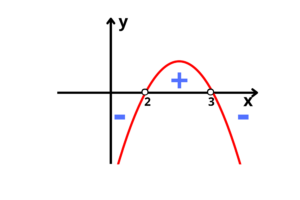
No interessam apenas os valores de $x$ que ao substituirmos na expressão, resulte em valores maiores que zero, portanto, as raízes não estão inclusas no conjunto solução. E como podemos visualizar acima, os números maiores que $2$ e menores que $3$, satisfazem essa condição
$$S:{x\,\epsilon\,\mathbb{R}/2<x<3}$$
Exemplo 4:
Resolva a inequação abaixo
$$x^2+2x+1>0$$
Montarmos uma equação equivalente e a resolvemos
$$x^2+2x+1=0$$
$$a=1, b=2, c=1$$
$$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$$
$$x=\frac{-2\pm\sqrt{2^2-4.1.1}}{2.1}$$
$$x=\frac{-2\pm\sqrt{0}}{2}$$
$$x=\frac{-2\pm0}{2}$$
$$x_1=\frac{-2+0}{2}=\frac{-2}{2}=-1$$
$$x_2=\frac{-2-0}{2}=\frac{-2}{2}=-1$$
Duas raízes reais e iguais, e o gráfico terá concavidade para cima
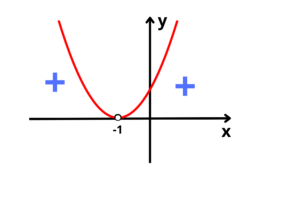
Como queremos apenas valores de $x$ que ao substituirmos na expressão, chegaremos em valores maiores que zero, nosso conjunto solução conterá todos os números reais, exceto o $-1$
$$S:{x\,\epsilon\,\mathbb{R}/x\neq-1}$$
Exemplo 5:
Resolva a inequação abaixo
$$-x^2-4x-4\leq0$$
Repetimos o processo feito anteriormente
$$-x^2-4x-4=0$$
$$a=-1, b=-4, c=-4$$
$$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$$
$$x=\frac{-(-4)\pm\sqrt{(-4)^2-4.(-1).(-4)}}{2.(-1)}$$
$$x=\frac{4\pm\sqrt{0}}{-2}$$
$$x=\frac{4\pm0}{-2}$$
$$x_1=\frac{4+0}{-2}=\frac{4}{-2}=-2$$
$$x_2=\frac{4-0}{-2}=\frac{4}{-2}=-2$$
Temos duas raízes reais e iguais, e o gráfico terá concavidade para baixo
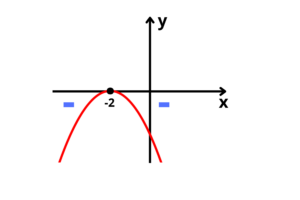
Como queremos apenas valores de $x$ que ao substituirmos na expressão, chegaremos em valores maiores que zero, nosso conjunto solução conterá todos os números reais, exceto o $-1$
$$S:{x\,\epsilon\,\mathbb{R}/x\neq-1}$$
Exemplo 5:
Resolva a inequação abaixo
$$-x^2-4x-4\leq0$$
Repetimos o processo feito anteriormente
$$-x^2-4x-4=0$$
$$a=-1, b=-4, c=-4$$
$$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$$
$$x=\frac{-(-4)\pm\sqrt{(-4)^2-4.(-1).(-4)}}{2.(-1)}$$
$$x=\frac{4\pm\sqrt{0}}{-2}$$
$$x=\frac{4\pm0}{-2}$$
$$x_1=\frac{4+0}{-2}=\frac{4}{-2}=-2$$
$$x_2=\frac{4-0}{-2}=\frac{4}{-2}=-2$$
Temos duas raízes reais e iguais, e o gráfico terá concavidade para baixo
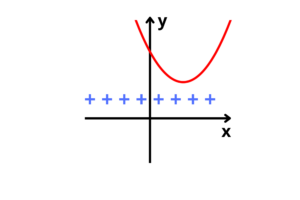
Não vai haver solução para essa inequação, pois independentemente do valor de $x$, ao substituirmos na expressão, não encontraremos valores menores que zero, apenas maiores. O conjunto solução é vazio, podendo ser representado de duas formas:
$$S:{}$$
ou
$$ S:{\phi}$$
Exemplo 7:
Resolva a inequação abaixo
$$-x^2+2x-7\geq0$$
Vamos montar e resolver a equação
$$-x^2+2x-7=0$$
$$a=-1, b=2, c=-7$$
$$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$$
$$x=\frac{-2\pm\sqrt{2^2-4.(-1).(-7)}}{2.(-1)}$$
$$x=\frac{-2\pm\sqrt{-24}}{-2}$$
Por fim, mas não menos importante, temos o último caso possível de inequação de segundo grau, onde as raízes não pertencem ao conjunto dos números reais e a concavidade é voltada para baixo
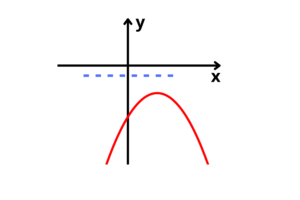
Não há valor que $x$ possa assumir que ao ser jogado na expressão, faça-a resultar em um número maior que zero, portanto, não há solução para a inequação
$$S:{}$$
Importância de estudar inequação
Muito parecida com a equação, mas com algumas peculiaridades, a inequação é um assunto recorrente em muitos assuntos da matemática, principalmente aqueles que envolvem funções. Além das aplicações citadas no início do artigo, para analisar o conteúdo dentro do módulo nas equações modulares, o entendimento sobre inequações pode vir a ser útil.
Formado em Eletrotécnica pelo IFRN, além de ter cursos de Matemática Básica e Cálculo pela empresa Help Engenharia.
