Função composta: O que é e como montá-la

Funções
ExercíciosTeoria
11/10/2024
Daniel Duarte

Juntamente com a função inversa, a função composta está presente na matéria de pré-cálculo em muitas faculdades, pois ela estará presente em todas as matérias de cálculo.

O que é uma função composta?

É uma função que é junção de duas ou mais funções, ela também é conhecida como “função de função” e serve para encurtar o caminho do cálculo de alguns valores e para podermos analisar funções complexas. Tomemos as funções $𝑓 (𝑥) = 𝑒 𝑥$ e $𝑔 (𝑥) = 𝑥 2$ , é possível formar duas funções compostas a partir delas:

1) Função $𝑓$ de $𝑔$ de $𝑥$

$𝑓 (𝑔 (𝑥)) = 𝑒 𝑥 2$

2) Função $𝑔$ de $𝑓$ de $𝑥$

$𝑔 (𝑓 (𝑥)) = 𝑒 2 𝑥$

Podemos ver acima as combinações entre a função exponencial e a função quadrática, elas não são feitas de qualquer forma, há um processo que deve ser respeitado e representações específicas para indicar que uma função é composta, como veremos nos próximos tópicos.

Como montar uma função composta?

Vamos revisar como achamos o valor de uma função qualquer, utilizemos para exemplo a função $𝑓 (𝑥) = 𝑥 2 - 4 𝑥 + 4$ , se quisermos calcular $𝑓 (3)$ , ou seja, o valor da função para $𝑥 = 3$ , temos que substituir o $3$ nos lugares onde tiver $𝑥$ na função

$𝑓 (𝑥) = 𝑥 2 - 4 𝑥 + 4$

$𝑓 (3) = 32 - 4.3 + 4$

$𝑓 (3) = 9 - 12 + 4$

$𝑓 (3) = 1$

E se ao invés de $3$ , quiséssemos calcular $𝑓 (𝑎)$ ? Faríamos o mesmo processo, colocamos o $𝑎$ onde tiver $𝑥$ na função

$𝑓 (𝑥) = 𝑥 2 - 4 𝑥 + 4$

$𝑓 (𝑎) = 𝑎 2 - 4 𝑎 + 4$

Então, seguindo esse raciocínio, se queremos calcular $𝑓 (𝑥 3 + 2)$ , substituímos essa expressão onde tiver a variável independente ( $𝑥$ )

$𝑓 (𝑥) = 𝑥 2 - 4 𝑥 + 4$

$𝑓 (𝑥 3 + 2) = (𝑥 3 + 2) 2 - 4 (𝑥 3 + 2) + 4$

$𝑓 (𝑥 3 + 2) = 𝑥 6 + 4 𝑥 3 + 4 - 4 𝑥 3 - 8 + 4$

$𝑓 (𝑥 3 + 2) = 𝑥 6$

Se você entendeu esse processo, então já sabes como montar uma função composta, e utilizarei um exemplo para comprovar isso.

Exemplo 1:

Dadas as funções $𝑓 (𝑥) = 𝑥 2 - 3 𝑥$ e $𝑔 (𝑥) = 𝑠 𝑒 𝑛 (𝑥)$ , calcule $𝑓 (𝑔 (𝑥))$

Bom, seguindo a lógica que abordamos agora há pouco, devemos substituir $𝑔 (𝑥)$ onde tivermos $𝑥$ na função $𝑓 (𝑥)$ , só que quem é $𝑔 (𝑥)$ ? O seno de $𝑥$ , portanto, devemos substituir o $𝑠 𝑒 𝑛 (𝑥)$

$𝑓 (𝑥) = 𝑥 2 - 3 𝑥$

$𝑓 (𝑔 (𝑥)) = (𝑠 𝑒 𝑛 (𝑥)) 2 - 3 . 𝑠 𝑒 𝑛 (𝑥)$

$𝑓 (𝑔 (𝑥)) = 𝑠 𝑒 𝑛 2 (𝑥) - 3 𝑠 𝑒 𝑛 (𝑥)$

Prontinho, calculamos uma função composta, a função “ $𝑓$ de $𝑔$ de $𝑥$ ”, e a representação é aquela que está no enunciado $𝑓 (𝑔 (𝑥))$ , onde a “função externa” é $𝑓 (𝑥)$ e a “função interna é $𝑔 (𝑥)$ . Mas e se a questão pedisse para calcularmos $𝑔 (𝑓 (𝑥))$ , o resultado seria o mesmo? Vamos calcular e ver se é isso mesmo. Dessa vez, substituiremos $𝑥 2 - 3 𝑥$ onde tiver $𝑥$ na função $𝑔 (𝑥)$

$𝑔 (𝑥) = 𝑠 𝑒 𝑛 (𝑥)$

$𝑔 (𝑓 (𝑥)) = 𝑠 𝑒 𝑛 (𝑥 2 + 3 𝑥)$

Chegamos em uma expressão totalmente diferente, e isso irá acontecer em quase todos os casos, pois a função composta não é comutativa, ou seja, alterar a ordem da combinação mudará a função que encontraremos.

Exemplo 2:

Dadas as funções $𝑓 (𝑥) = \sqrt 𝑥$ , $𝑔 (𝑥) = 𝑥 - 4$ e $ℎ (𝑥) = 𝑒 𝑥$ , calcule $𝑓 (𝑔 (ℎ (𝑥)))$

Agora temos três funções, o método em si será igual, no entanto, precisamos nos atentar a um detalhe, quando tivermos que calcular uma função composta formada por três ou mais funções, precisamos começar pela função mais interna e depois iremos para as mais externas. No exemplo acima, primeiros devemos calcular $𝑔 (ℎ (𝑥))$ e o resultado disso, substituiremos onde tiver $𝑥$ na função $𝑓 (𝑥)$ , calculando assim a função $𝑓 (𝑔 (ℎ (𝑥)))$

1) Calculando $𝑔 (ℎ (𝑥))$

$𝑔 (𝑥) = 𝑥 - 4$

$𝑔 (ℎ (𝑥)) = 𝑒 𝑥 - 4$

2) Calculando $𝑓 (𝑔 (ℎ (𝑥)))$

$𝑓 (𝑥) = \sqrt 𝑥$

$𝑓 (𝑔 (ℎ (𝑥))) = \sqrt 𝑒 𝑥 - 4$

É comum encontrarmos outra representação para a função composta, por exemplo: “Calcule $𝑓 \circ 𝑔$ …” Esse $𝑓 \circ 𝑔$ é a mesma coisa que $𝑓 (𝑔 (𝑥))$ , então, poderíamos representar a função que encontramos nessa questão assim:

$𝑓 \circ 𝑔 \circ ℎ = \sqrt 𝑒 𝑥 - 4$

Nessa representação fica fácil identificar quem é a função mais interna, pois é a que fica à direita de todas as outras.

Valor numérico de uma função composta

Calcular o valor numérico de uma função composta é muito simples, pois basta substituirmos o valor que queremos calcular onde tiver a variável independente, coisa que revisamos no tópico passado.

Exemplo 1:

Dada a função $𝑓 (𝑔 (𝑥)) = \sqrt 𝑥 3 - 2$ , calcule $𝑓 (𝑔 (3))$

Devemos substituir $3$ onde tiver $𝑥$ e simplificar ao máximo a expressão resultante

$𝑓 (𝑔 (𝑥)) = \sqrt 𝑥 3 - 2$

$𝑓 (𝑔 (3)) = \sqrt 33 - 2$

$𝑓 (𝑔 (3)) = \sqrt 27 - 2$

$𝑓 (𝑔 (3)) = \sqrt 25$

$𝑓 (𝑔 (3)) = 5$

Isso por si só não parece grande coisa, mas a função composta nos permite economizar passos em um cálculo, pois digamos que tivéssemos as funções $𝑓 (𝑥) = \sqrt 𝑥$ e $𝑔 (𝑥) = 𝑥 3 - 2$ , e fosse pedido para calcular $𝑔 (3)$ e depois pegar o resultado disso e substituir em $𝑓 (𝑥)$ , teríamos que realizar dois passos, só que a função do exercício que acabamos de resolver fez justamente isso, de uma vez só. Pode parecer confuso, mas mostrarei um exemplo para ficar claro.

Exemplo 2:

Dadas as funções $𝑓 (𝑥) = 𝑥 2$ e $𝑔 (𝑥) = 𝑥 + 3$ , calcule $𝑔 (2)$ e em seguida substitua o resultado na função $𝑓 (𝑥)$ . Determine $𝑓 (𝑔 (𝑥))$ e calcule $𝑓 (𝑔 (2))$ e compare os resultados.

Vamos cumprir o primeiro comando da questão

$𝑔 (𝑥) = 𝑥 + 3$

$𝑔 (2) = 2 + 3$

$𝑔 (2) = 5$

$𝑓 (𝑥) = 𝑥 2$

$𝑓 (5) = 52$

$𝑓 (5) = 25$

Agora, vamos montar a função composta $𝑓 (𝑔 (𝑥))$ e calcular $𝑓 (𝑔 (2))$

$𝑓 (𝑥) = 𝑥 2$

$𝑓 (𝑔 (𝑥)) = (𝑥 + 3) 2$

$𝑓 (𝑔 (2)) = (2 + 3) 2$

$𝑓 (𝑔 (2)) = 52$

$𝑓 (𝑔 (2)) = 25$

Chegamos no mesmo valor, só que com um passo à menos, imagina o quanto poderíamos economizar se tivéssemos uma função composta com três ou mais funções.

Diagrama da função composta

Geralmente é utilizado um diagrama (representação gráfica) para mostrar o que foi explicado no tópico anterior, só que ele mostra de forma geral, considerando quaisquer valores para a variável independente:

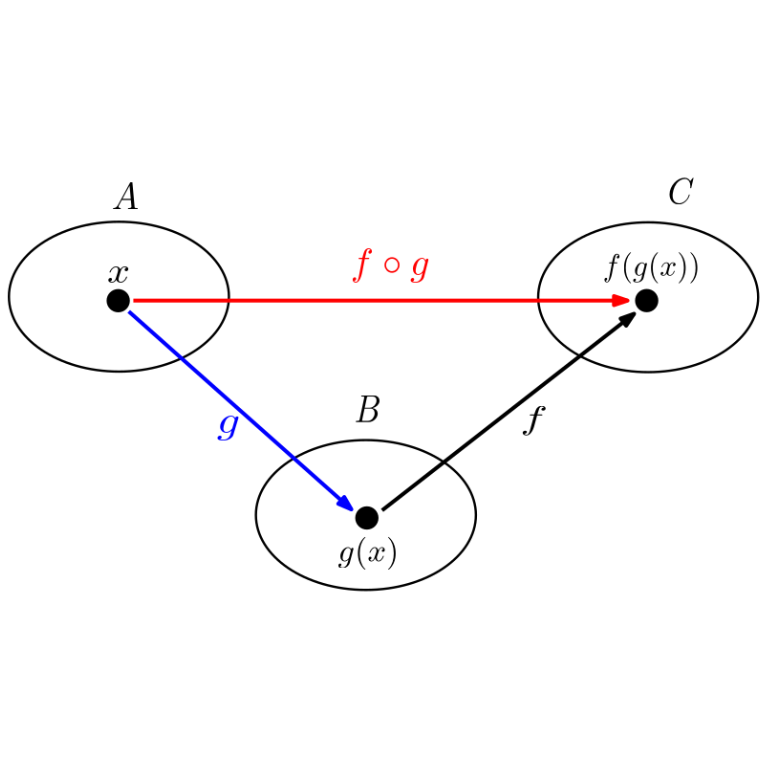
Função composta de funções inversas

Se estais com a memória boa, lembrará que falei anteriormente que a ordem de cálculo das funções inversas altera o resultado, mas que isso se aplicava a quase todos os casos, uma das exceções, que é quando calculamos funções compostas de funções que são inversas, nesse caso, independentemente de como calculemos a composta, ela será igual à função identidade.

Exemplo:

Dadas as funções $𝑓 (𝑥) = 𝑙 𝑜 𝑔 2 𝑥$ e $𝑔 (𝑥) = 2 𝑥$ , calcule $𝑓 (𝑔 (𝑥))$ e $𝑔 (𝑓 (𝑥))$

A função logarítmica é inversa da função exponencial, portanto, ambas as compostas devem ter o mesmo resultado ( $ℎ (𝑥) = 𝑥$ , função identidade)

1) Calculando $𝑓 (𝑔 (𝑥))$

$𝑓 (𝑥) = 𝑙 𝑜 𝑔 2 𝑥$

$𝑓 (𝑔 (𝑥)) = 𝑙 𝑜 𝑔 2 2 𝑥$

$𝑓 (𝑔 (𝑥)) = 𝑥 . 𝑙 𝑜 𝑔 2 2$

$𝑓 (𝑔 (𝑥)) = 𝑥 . 1$

$𝑓 (𝑔 (𝑥)) = 𝑥$

2) Calculando $𝑔 (𝑓 (𝑥))$

$𝑔 (𝑥) = 2 𝑥$

$𝑔 (𝑓 (𝑥)) = 2 𝑙 𝑜 𝑔 2 𝑥$

$𝑔 (𝑓 (𝑥)) = 𝑥$

Gráfico de uma função composta

Há uma infinidade de possibilidades de funções compostas, logo, também existem infinitos gráficos possíveis com comportamentos completamente diferentes, então não faz sentido e nem é possível desenvolver uma técnica para desenhar todos esses gráficos, sendo necessária a utilização de softwares para a visualização deles. Mas para os curiosos de plantão, irei mostrar os gráficos de duas funções simples e de suas possíveis combinações.

1) Gráfico da função $𝑓 (𝑥) = 𝑠 𝑒 𝑛 (𝑥)$

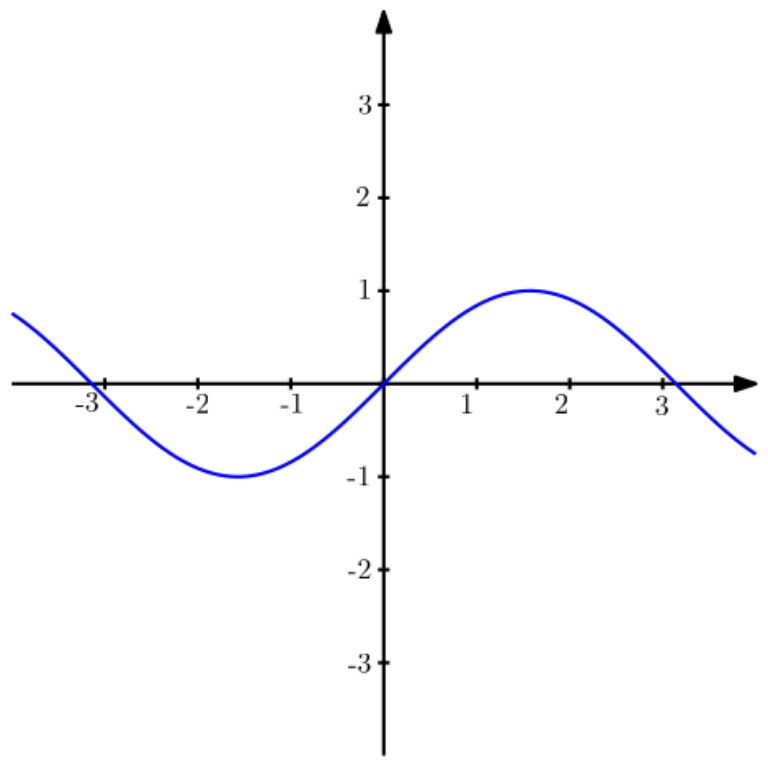
2) Gráfico da função $𝑔 (𝑥) = 𝑒 𝑥$

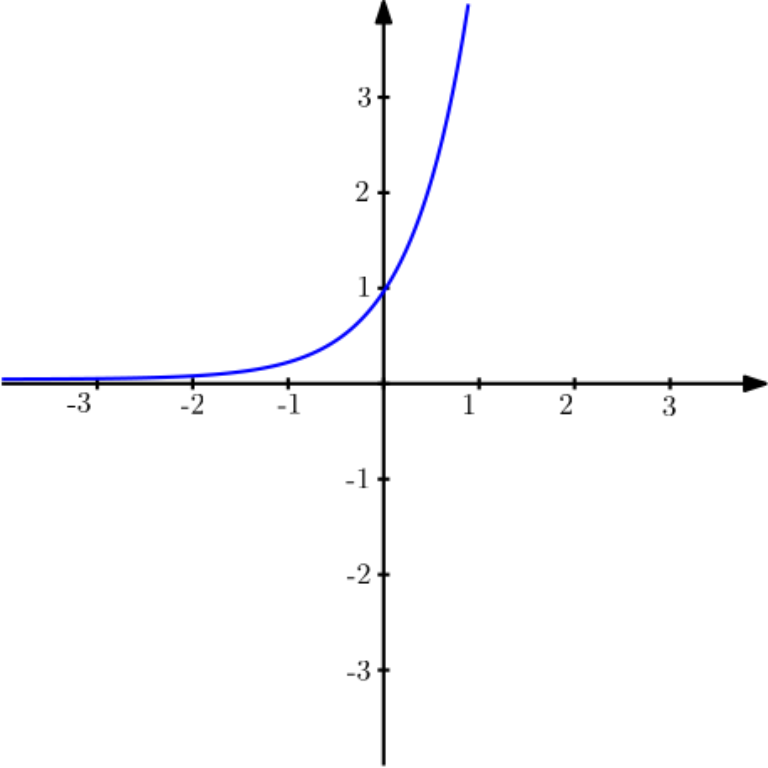
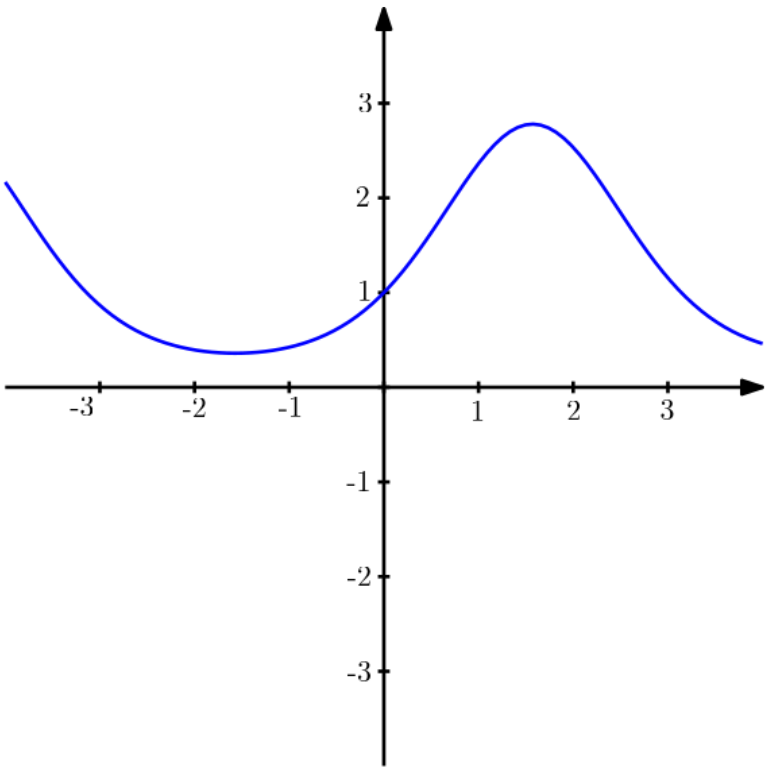
3) Gráfico da função $𝑓 (𝑔 (𝑥)) = 𝑠 𝑒 𝑛 (𝑒 𝑥)$

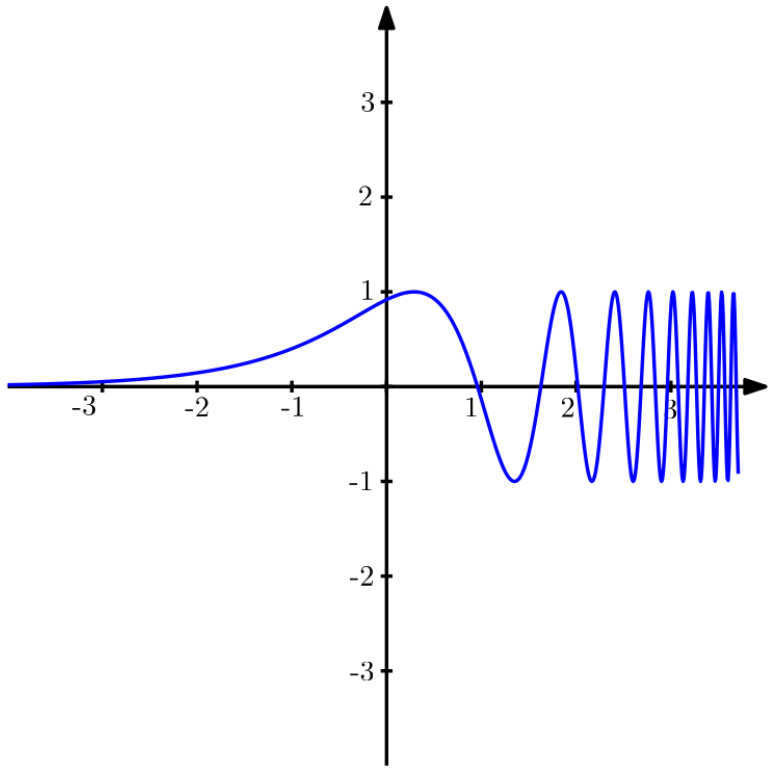
4) Gráfico da função $𝑔 (𝑓 (𝑥)) = 𝑒 𝑠 𝑒 𝑛 (𝑥)$

Exercícios resolvidos de função composta

1. Dadas as funções $𝑓 (𝑥) = 𝑙 𝑛 | 𝑥 |$ e $𝑔 (𝑥) = 𝑠 𝑒 𝑛 (𝑥 + 2)$ , determine $𝑓 \circ 𝑔$ e $𝑔 \circ 𝑓$

Primeiramente calculamos $𝑓 \circ 𝑔$

$𝑓 (𝑥) = 𝑙 𝑛 | 𝑥 |$

$𝑓 \circ 𝑔 = 𝑙 𝑛 | 𝑠 𝑒 𝑛 (𝑥 + 2) |$

Por fim, calculamos $𝑔 \circ 𝑓$

$𝑔 (𝑥) = 𝑠 𝑒 𝑛 (𝑥 + 2)$

$𝑔 \circ 𝑓 = 𝑠 𝑒 𝑛 (𝑙 𝑛 | 𝑥 | + 2)$

2. Dadas as funções $𝑓 (𝑥) = 𝑥 2 - 4$ e $𝑔 (𝑥) = \sqrt 𝑥$ , calcule $𝑓 (𝑔 (16))$

Podíamos calcular $𝑔 (16)$ e depois jogarmos o resultado em $𝑓 (𝑥)$ , no entanto, podemos calcular $𝑓 (𝑔 (𝑥))$ e aí sim substituímos o $16$ onde tiver $𝑥$ na função composta

$𝑓 (𝑥) = 𝑥 2 - 4$

$𝑓 (𝑔 (𝑥)) = (\sqrt 𝑥) 2 - 4$

$𝑓 (𝑔 (𝑥)) = 𝑥 - 4$

$𝑓 (𝑔 (16)) = 16 - 4$

$𝑓 (𝑔 (16)) = 12$

3. Dadas as funções $𝑓 (𝑥) = \sqrt 𝑥 - 2$ , $𝑔 (𝑥) = 2 𝑥$ e $ℎ (𝑥) = 𝑥 2 + 𝑠 𝑒 𝑛 (𝑥)$ , calcule $𝑔 \circ ℎ \circ 𝑓$

Começaremos calculando $ℎ \circ 𝑓$

$ℎ (𝑥) = 𝑥 2 + 𝑠 𝑒 𝑛 (𝑥)$

$ℎ \circ 𝑓 = (\sqrt 𝑥 - 2) 2 + 𝑠 𝑒 𝑛 (\sqrt 𝑥)$

$ℎ \circ 𝑓 = 𝑥 - 2 + 𝑠 𝑒 𝑛 (\sqrt 𝑥)$

Agora calcularmos $𝑔 \circ ℎ \circ 𝑓$ , sempre um passo de cada vez

$𝑔 (𝑥) = 2 𝑥$

$𝑔 \circ ℎ \circ 𝑓 = 2 𝑥 - 2 + 𝑠 𝑒 𝑛 (\sqrt 𝑥)$

Daniel Duarte

Formado em Eletrotécnica pelo IFRN.

Sobre nós

O Matematiquês é um blog dedicado ao aprendizado de matemática, e nosso objetivo é tornar o ensino mais acessível e envolvente através de conteúdos de alta qualidade e gratuitos para alunos e professores em todo o Brasil. Buscamos simplificar conceitos complexos com uma abordagem clara e direta, priorizando transparência, diversidade, clareza, qualidade, inovação e compromisso social. Nosso blog oferece conteúdos fundamentados por especialistas, revisados com rigor e atualizados.

Categorias

Posts mais recentes

All Post
Curiosidades
Ensino Fundamental
Ensino Médio
Ensino Superior
Livros
Notícias

Back
Cinemática
Dinâmica
Conceitos básicos da física

Back
Conceitos básicos da matemática
Frações
Potenciação
Radiciação
Geometria plana
Logaritmo

Back
Funções
Equações
Conjuntos numéricos
Geometria espacial
Inequações
Módulo
Progressões matemáticas
Física
Trigonometria
Cinemática
Dinâmica
Conceitos básicos da física

Back
Limites
Derivadas
Integrais
Equações Diferenciais
Vetores e Geometria Analítica

Função composta: O que é e como montá-la

O que é uma função composta?

Como montar uma função composta?

Valor numérico de uma função composta

Diagrama da função composta

Função composta de funções inversas

Gráfico de uma função composta

Exercícios resolvidos de função composta

Sobre nós

Categorias

Posts mais recentes

Artur Ávila: Biografia

IFPR Abre Inscrições para Cursos de Licenciatura Gratuitos em 2026

Unicamp abre vagas para segunda fase do seu vestibular 2026!

Tags

Matematiquês © 2024. Todos os direitos reservados.