O que é o módulo?
Podemos dizer que o módulo é um dispositivo matemático que serve para garantir que um determinado valor seja sempre positivo, em outras palavras, ao aplicarmos o módulo em um valor qualquer, o resultado será esse mesmo valor só que positivo. A representação do módulo são duas barrinhas verticais em volta de um número (ou letra).
$$|a|$$
Se um número positivo estiver dentro de um módulo, ele continuará sendo positivo ($|a|=a$)
Exemplos:
1) $|3|=3$
2) $|5|=5$
3) $|10|=10$
E caso ele seja negativo, ao se aplicar o módulo (quando sumirem as barrinhas) ele se tornará positivo ($|-a|=-(-a)=a$)
Exemplos:
1) $|-1|=1$
2) $|-2|=2$
3) $|-\pi|=\pi$
Podes estar se perguntando sobre o zero, só que como ele é um número neutro, aplicar o módulo nele não irá alterá-lo em nada.
Mas em termos matemáticos, o que é o módulo? Também chamado de “valor absoluto”, é a distância na reta numérica entre um número e o zero, e como a distância não pode ser uma medida negativa, esse valor é sempre positivo, mesmo que a distância calculada seja entre um número negativo e o zero.
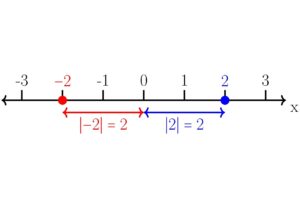
Na foto acima, tanto o $2$, quanto o $-2$ possuem a mesma distância até o zero, portanto, dizemos que eles possuem “o mesmo valor em módulo”, isso acontece com qualquer número e seu oposto.
Exemplos:
1) $|7|=|-7|=7$
2) $|-12|=|12|=12$
3) $|-0|=|0|=0$
Como a distância de zero até o próprio zero na reta numérica é de zero unidades, nada mais justo que seu valor absoluto (módulo) ser igual a zero. O módulo só impactará os cálculos significativamente, a ponto de termos que analisar o que acontece ao aplicarmos ele na equação modular (ou função modular) ou especificamente quando ele estiver sendo aplicado em uma variável.
