Pode-se dizer que o Teorema de Pitágoras é um dos conceitos matemáticos mais famosos e utilizados da história. Caso não tenhas aprendido ainda, venha tirar suas dúvidas com esse artigo completinho sobre esse teorema muito útil.
O que é o Teorema de Pitágoras?
É um dos conceitos fundamentais da geometria, ele relaciona os comprimentos dos lados de um triângulo retângulo. O teorema diz que “o quadrado da hipotenusa é igual à soma dos quadrados dos catetos”, em outras palavras, o comprimento do lado oposto ao ângulo de $90°$ ao quadrado (hipotenusa) é igual à soma dos comprimentos dos demais lados (catetos), elevados ao quadrado. A equação clássica que representa esse teorema é:
$$c^2=a^2+b^2$$,
Onde $c$ é a hipotenusa, e $a$ e $b$ são os catetos.
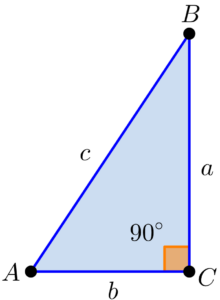
Este teorema é essencial para calcular distâncias e resolver problemas geométricos.
Como usar o Teorema de Pitágoras?
Para usá-lo precisamos de um triângulo retângulo, e para identificar um, precisamos olhar para o símbolo que representa um de seus ângulos, se houver um quadrado em um dos cantos, significa que é um ângulo reto (de $90°$), portanto, o triângulo em questão é retângulo.
Geralmente utilizamos o teorema de Pitágoras para descobrir o comprimento de um dos lados de um triângulo retângulo, uma vez que conhecemos o comprimento dos outros dois, então nos resta aplicar a equação e isolar o lado que queremos descobrir o comprimento.
Exemplo: Calcule o perímetro do triângulo abaixo
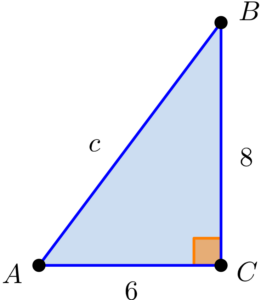
Para calcular o perímetro de uma figura geométrica, somamos todos os comprimentos dos seus lados. Primeiramente, identificaremos quem precisamos calcular. Como o lado $c$ está oposto ao ângulo reto, teremos que achar o comprimento da hipotenusa, nos restando a aplicação direta da equação
$$c^2=a^2+b^2$$
$$c^2=8^2+6^2$$
$$c^2=64+36$$
$$c^2=100$$
$$c=\sqrt{100}$$
$$c=10$$
Apesar de estarmos resolvendo uma equação, só consideramos a solução positiva dessa raiz quadrada, pois não existe medida de comprimento negativa. Para finalizar a questão, somamos os comprimentos e achamos o perímetro pedido
$$P=a+b+c$$
$$P=8+6+10$$
$$P=24$$
O que é o Triângulo Pitagórico?
Esse é o nome dado a um triângulo retângulo cujos lados possuem comprimentos iguais a números inteiros. Os conjuntos de números que formam tais triângulos são chamados de triplas pitagóricas. O exemplo mais famoso é o triângulo $3$, $4$, $5$, quando você identificar que um triângulo possui dois lados que são múltiplos desses valores, basta descobrir qual o fator de proporcionalidade e com isso você poderá achar facilmente o valor do terceiro lado.
No exercício anterior, tínhamos um triângulo pitagórico, os catetos eram múltiplos de $3$ e $4$, e o fator de proporcionalidade era $2$, portanto, a hipotenusa dele seria $5$ vezes esse fator, que resulta em $10$, como encontramos através do Teorema de Pitágoras.
Relação entre o Teorema de Pitágoras e os Números Irracionais
O Teorema de Pitágoras foi crucial para o desenvolvimento dos números irracionais. Ao calcular a hipotenusa usando $$a^2+b^2=c^2$$, muitas vezes o resultado não é um número inteiro nem uma fração, mas um número irracional. Um exemplo clássico é a hipotenusa de um triângulo com lados $1$ e $1$, cujo comprimento é $\sqrt{2}$, um número irracional.
Demonstração do Teorema de Pitágoras: Método visual
Para os entusiastas da matemática, mostrarei uma das demonstrações clássicas do Teorema de Pitágoras, que envolve o uso de áreas geométricas. A seguir, descreverei o passo a passo dessa demonstração:
Passo 1: Desenhar o Triângulo Retângulo
Começamos com um triângulo retângulo com lados $a$, $b$, e hipotenusa $c$.
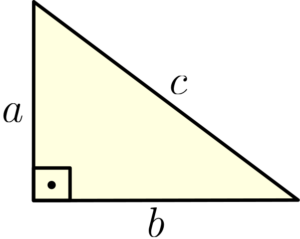
Passo 2: Construir quadrados sobre cada lado
Desenhamos um quadrado de lado $c$ sobre a hipotenusa. A área desse quadrado é $c^2$. Em seguida, desenhamos um quadrado de lado $a$ e outro de lado $b$. As áreas desses quadrados são $a^2$ e $b^2$, respectivamente.
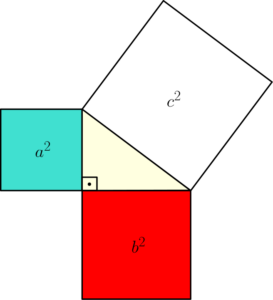
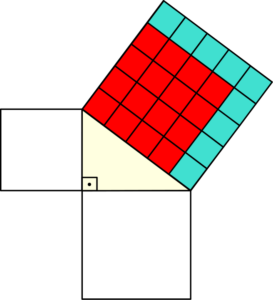
Passo 3: Reorganizar as áreas
Agora “quebramos” os quadrados $a^2$ e $b^2$ e reorganizamos para formar o quadrado maior $c^2$.
História resumida sobre Pitágoras
Pitágoras de Samos, foi um filósofo e matemático grego do século VI a.C., e lhe é frequentemente creditada a formulação do teorema que leva seu nome, apesar de evidências sugerirem que era conhecido por matemáticos babilônios. Além da matemática, Pitágoras fundou uma escola que combinava religião e ciência. Sua figura é envolta em lendas, incluindo a crença em transmigração de almas e a harmonia das esferas.
Exercícios Resolvidos de Teorema de Pitágoras
1. Um triângulo tem hipotenusa de $13$ e um lado de $5$. Encontre o outro lado.
Precisamos descobrir o valor de um dos catetos, podemos chamá-lo de $a$, agora é só aplicarmos o teorema e isolarmos o $a$
$$a^2+b^2=c^2$$
$$a^2+5^2=13^2$$
$$a^2+25=169$$
$$a^2=169-25$$
$$a^2=144$$
$$a=\sqrt{144}$$
$$a=12$$
2. Verifique se o triângulo com lados $7$, $24$, $25$ é retângulo.
Para verificarmos se um triângulo é retângulo, podemos utilizar o próprio teorema de Pitágoras, pois caso ele se prove verdadeiro, significa que o triângulo é retângulo. Detalhe importante: A hipotenusa sempre será o maior lado do triângulo retângulo, então na hora de substituirmos na equação, a hipotenusa valerá $25$.
$$a^2+b^2=c^2$$
$$7^2+24^2=25^2$$
$$49+576=625$$
$$625=625$$
Sim, é um triângulo retângulo.
Formado em Eletrotécnica pelo IFRN, além de ter cursos de Matemática Básica e Cálculo pela empresa Help Engenharia.
