A irracionalidade da raiz quadrada de $2$ é um resultado matemático clássico que remonta à Grécia Antiga. Sua demonstração é uma das primeiras evidências de que existem números que não podem ser expressos como uma fração entre dois inteiros. Neste artigo, exploraremos o conceito de irracionalidade, discutiremos brevemente sua história e apresentaremos a demonstração clássica por redução ao absurdo.
O que é um número irracional?
Um número irracional é aquele que não pode ser escrito como uma razão entre dois números inteiros, ou seja, não pode ser expresso na forma $\frac{p}{q}$, com $p$ e $q$ inteiros e $q \neq 0$. Exemplos de números irracionais incluem $\pi$, $e$ (o número de Euler) e $\sqrt{2}$.
A história do quadrado de lado 1
A jornada que leva à descoberta da irracionalidade de $\sqrt{2} $ está intimamente ligada a um problema geométrico simples. Considere um quadrado de lado $1$.
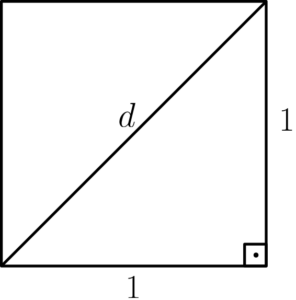
A questão central é calcular o comprimento da diagonal desse quadrado. Usando o Teorema de Pitágoras, sabemos que, para um quadrado com lados de comprimento $1$, a diagonal $d$ satisfaz a equação:
$$d^2=1^2+1^2$$
$$\Rightarrow d^2=2$$
$$\Rightarrow d= \pm \sqrt{2}$$
Como estamos tratando de uma medida de comprimento, consideramos apenas a solução positiva. Portanto, a diagonal do quadrado tem comprimento $d= \sqrt{2}$.
Agora, surge a pergunta: será que $\sqrt{2}$ pode ser expresso como uma razão de dois inteiros? Em outras palavras, será que $\sqrt{2}$ é um número racional? A resposta é não, e a descoberta dessa irracionalidade causou um grande impacto na história da matemática. Os pitagóricos acreditavam que todos os números poderiam ser expressos como frações de inteiros, ou seja, como números racionais. Quando a irracionalidade de $\sqrt{2}$ foi descoberta, ela se tornou uma das primeiras evidências de que os números racionais não eram suficientes para descrever todos os aspectos da realidade matemática. Essa constatação abalou a visão pitagórica de que a matemática, em sua totalidade, fosse exclusivamente composta por números racionais. A descoberta de $\sqrt{2}$ mostrou que, além dos números racionais, existiam outros tipos de números, os irracionais, ampliando significativamente a compreensão dos matemáticos sobre os números e sobre a própria matemática.
Demonstração da irracionalidade de $\sqrt{2}$
A demonstração mais conhecida de que $ \sqrt{2} $ é irracional utiliza o método da redução ao absurdo. A ideia é supor que $ \sqrt{2} $ é racional e mostrar que essa suposição leva a uma contradição.
Suponha, por absurdo, que $ \sqrt{2} $ seja um número racional. Isso significa que ele pode ser expresso como uma fração $ \sqrt{2} = \frac{p}{q} $, onde $ p, q \in \mathbb{Z} $, $ q \neq 0 $, e $ p $ e $ q $ não têm fatores comuns, ou seja, $ \text{MDC}(p, q) = 1 $. Em outras palavras, $ p $ e $ q $ são números inteiros, $ q $ é diferente de zero e a fração está na sua forma irredutível, ou seja, não pode ser simplificada. Assim, elevando ambos os lados da equação ao quadrado, obtemos: $$ 2 = \frac{p^2}{q^2}. $$
Multiplicando ambos os lados por $ q^2 $, segue que:
$$ p^2 = 2q^2. $$
A equação acima mostra que $ p^2 $ é um número par, pois é igual a $ 2q^2 $ (um múltiplo de 2). Ora, se $ p^2 $ é par, então $ p $ também é par, por propriedades dos números inteiros. Logo, podemos escrever $ p = 2k $, com $ k \in \mathbb{Z} $, já que $ p $ é par. Substituindo $ p = 2k $ na equação $ p^2 = 2q^2 $:
$$ (2k)^2 = 2q^2 $$
$$ \Rightarrow 4k^2 = 2q^2. $$
Dividindo ambos os lados da equação por 2, obtemos:
$$ 2k^2 = q^2. $$
Daí concluímos que $ q^2 $ também é par, logo $ q $ é par. Porém, isso é um absurdo, pois se $ p $ e $ q $ são ambos pares, a fração $ \frac{p}{q} $ não é irredutível. Poderíamos simplificar a fração por 2, o que contraria nossa suposição inicial de que $ \frac{p}{q} $ está na forma irredutível. Portanto, a suposição de que $ \sqrt{2} $ é racional é falsa. Concluímos, assim, que $ \sqrt{2} $ é irracional.
Licenciado em Matemática pela UEPB. Pós-graduando em Modelagem Matemática e Cálculo Avançado.
