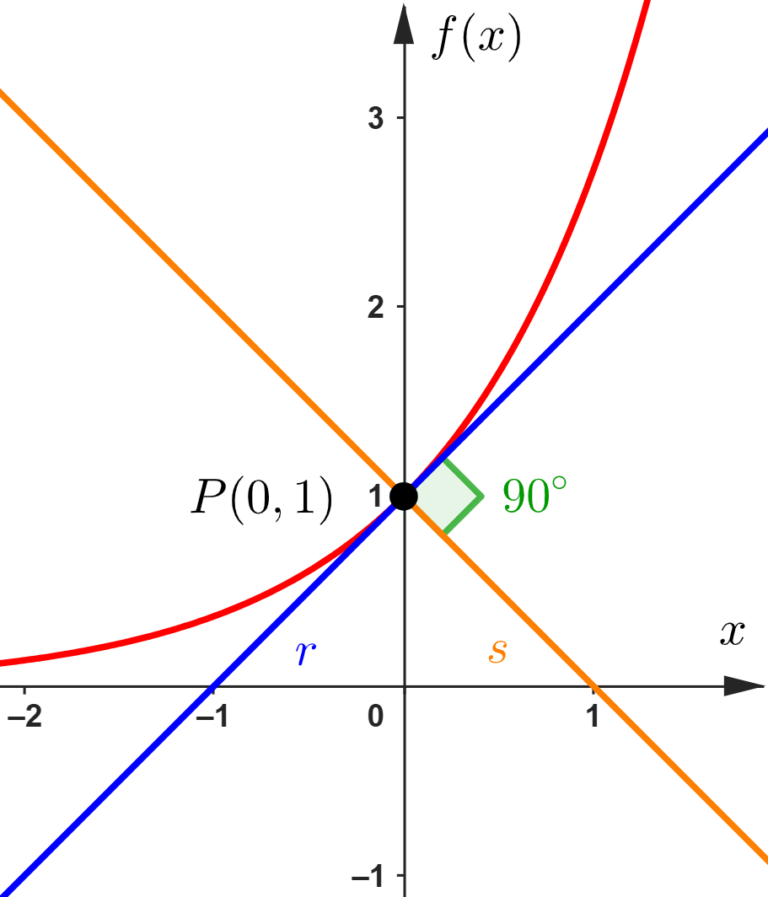
Além da derivada representar a taxa de variação instantânea de uma função, ela também é a inclinação da função em um determinado ponto (caso queira entender o porquê, confira nosso outro artigo sobre a derivada ser a inclinação da função). A partir disso, podemos achar duas retas auxiliares que podem ajudar na análise de uma função, e é sobre isso que falarei neste artigo.
O que é uma reta tangente?
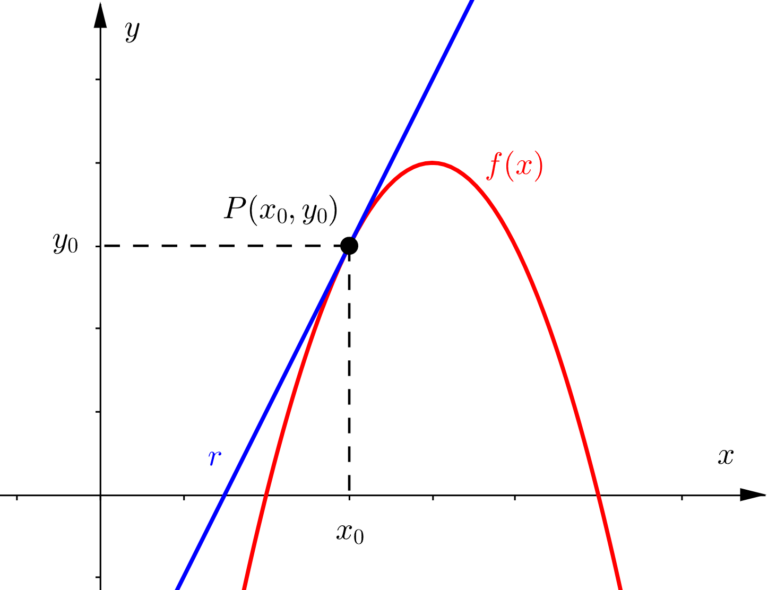
Dizemos que uma reta é tangente a uma curva, quando ela toca essa curva em um único ponto, isso explica a expressão “tangenciar”, que é usada em contextos onde algo toca outra coisa de forma muito sutil, de forma leve, quase imperceptível. Quando trabalhamos com funções, podemos chamar a figura formada pelo gráfico da função de “curva de uma função” (fica a observação que na matemática, uma reta também é uma curva, achei importante mencionar, pois no dia a dia é comum associarmos a palavra “curva” com coisas arredondadas). Assim, quando queremos achar a reta tangente à curva da função em um ponto, significa que precisamos achar a equação da reta tangente que toca o gráfico da função nesse ponto específico.
Tomemos uma função
O que é uma reta normal?
Tanto na matemática quanto na física, quando falamos que algum elemento (reta, vetor, figura) é “normal” em relação a outra coisa, queremos dizer que ele é perpendicular a essa coisa, ou seja, forma uma ângulo de noventa graus (ângulo reto). Então, se eu digo que uma reta é normal a outra reta, significa que o ângulo formado entre elas é de
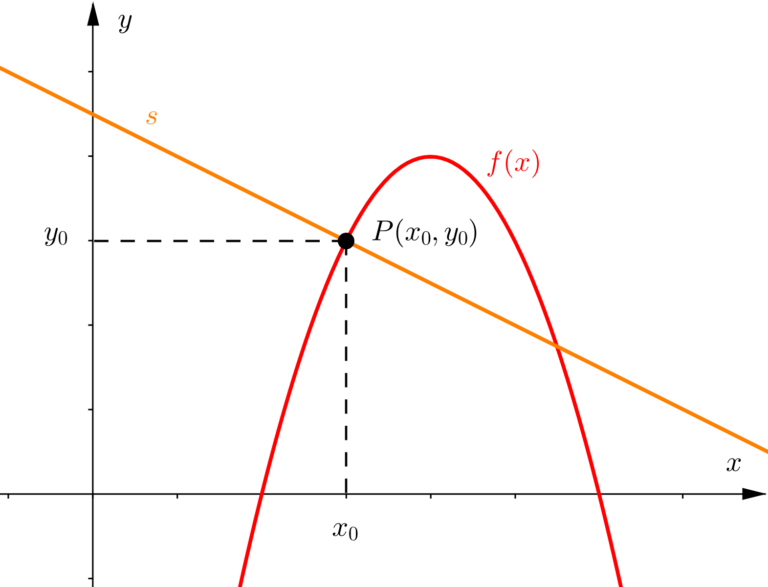
Um fato curioso e importante (guarde essa informação, pois a usarei posteriormente), é que a reta tangente em um ponto é perpendicular à reta normal nesse mesmo ponto.
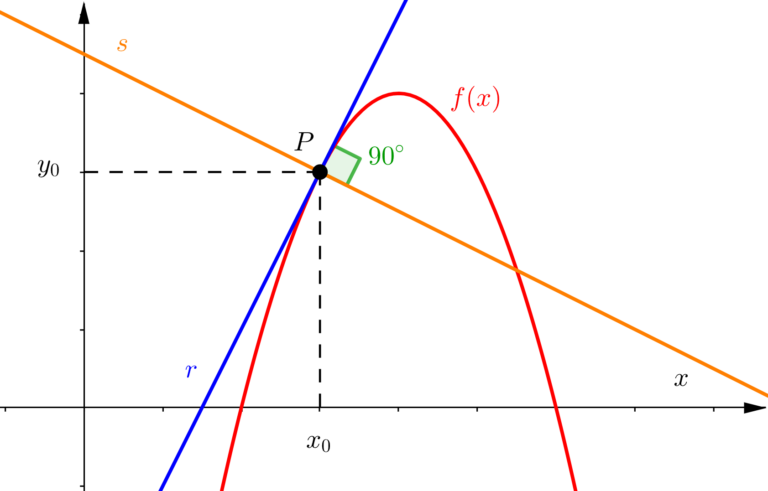
Isso irá acontecer com todas as retas tangentes e normais para quaisquer pontos no gráfico da função.
Como calcular as equações das retas tangente e normal?
Resumidamente, a derivada de uma função em um determinado ponto é igual ao coeficiente angular da reta tangente a esse mesmo ponto, por sua vez, o coeficiente angular indica quão inclinada uma reta está, quanto maior for o valor dele, mais inclinada ela estará (simplificadamente, a inclinação da reta é o ângulo que ela faz com o eixo horizontal, então, quanto maior o coeficiente angular, maior o ângulo entre a reta tangente e o eixo
Onde
Exemplo 1: Ache a equação da reta tangente à curva da função
Primeiramente, precisamos entender o que a questão está pedindo, e para isso, vamos desenhar o gráfico da função quadrática que a questão nos deu (se não souber montar o gráfico, dá uma olhada no nosso artigo sobre função de
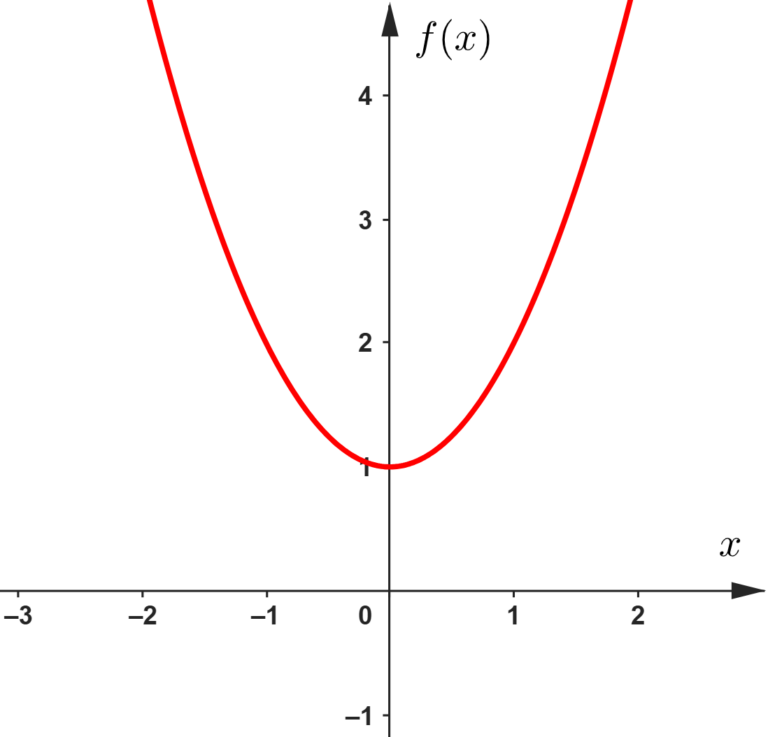
Para marcar o ponto
Portanto, o ponto ao qual a questão se refere é o ponto
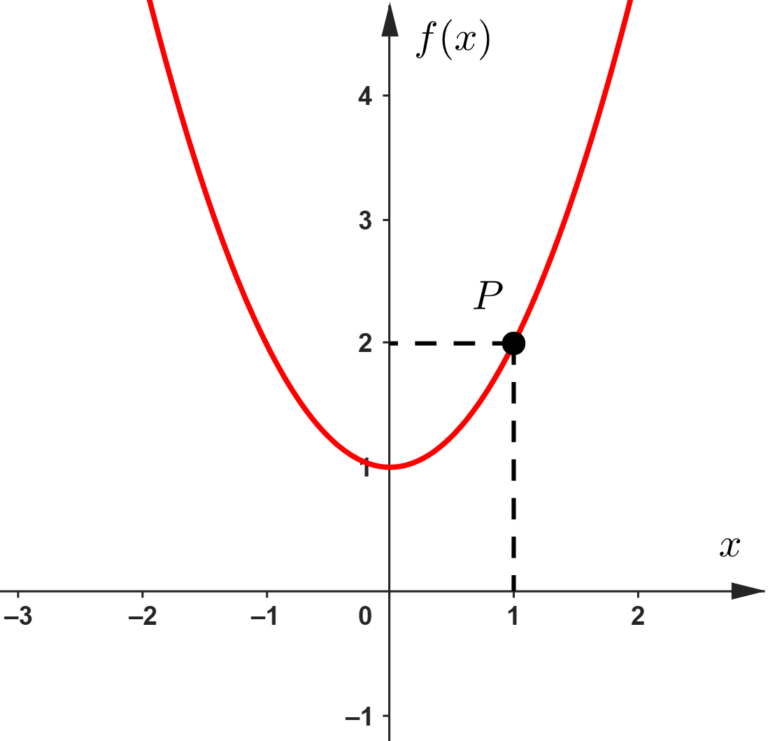
A questão está nos pedindo a equação da reta tangente a esse ponto, ou seja, quer a equação da reta que toca a função apenas nesse ponto
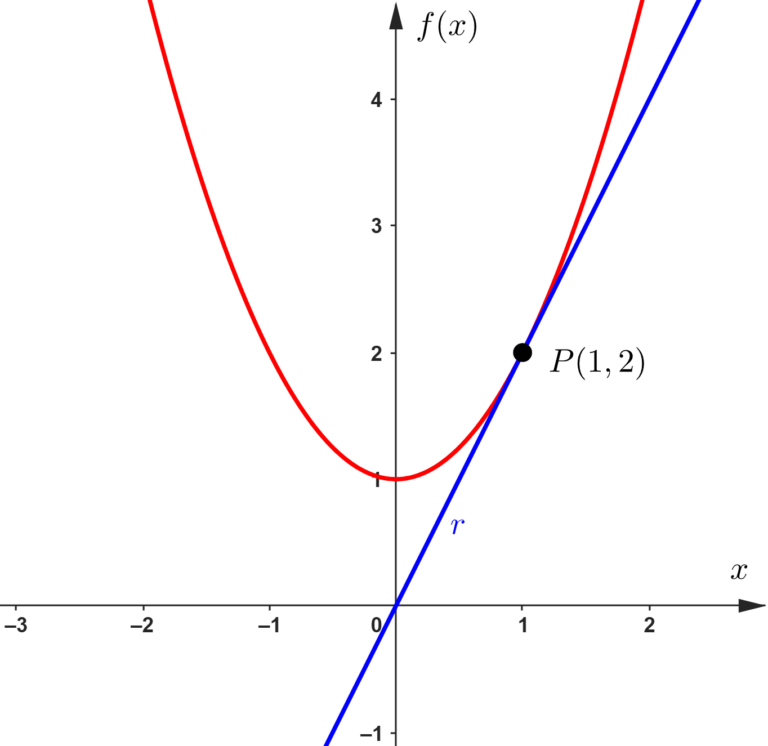
Chamei a reta de
O
Já temos
Portanto, a equação da reta tangente à curva da função
Exemplo 2: Ache a equação da reta normal à curva da função
Primeiramente, vamos desenhar o gráfico da função exponencial
Para marcar o ponto no gráfico, precisamos calcular sua coordenada no eixo
O ponto que a questão se refere é
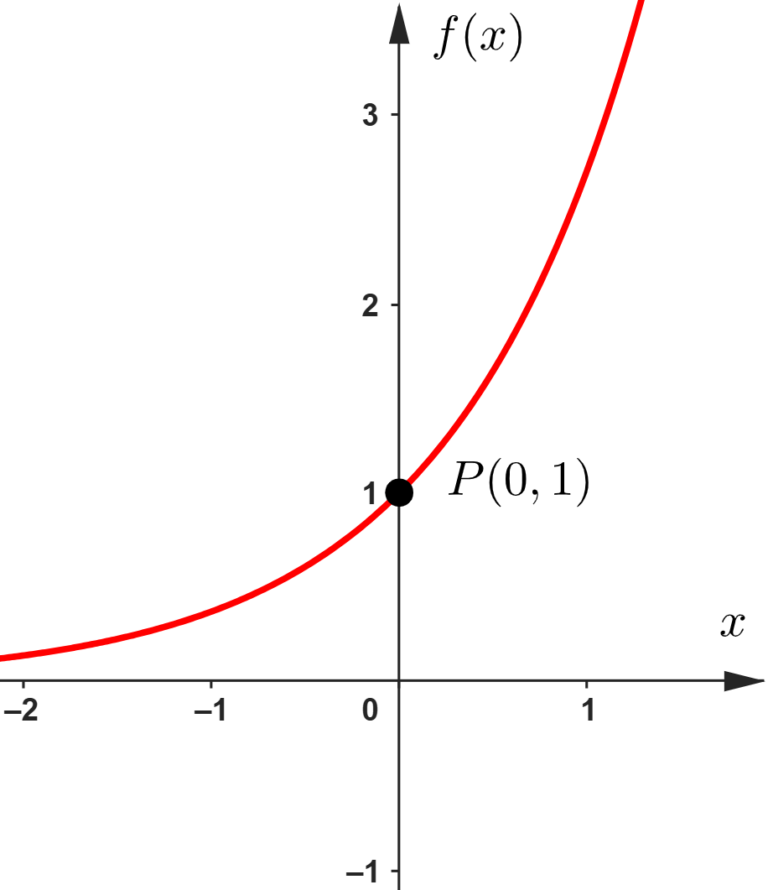
Queremos encontrar a equação da reta normal à curva nesse ponto, que representarei no gráfico (chamarei ela de reta
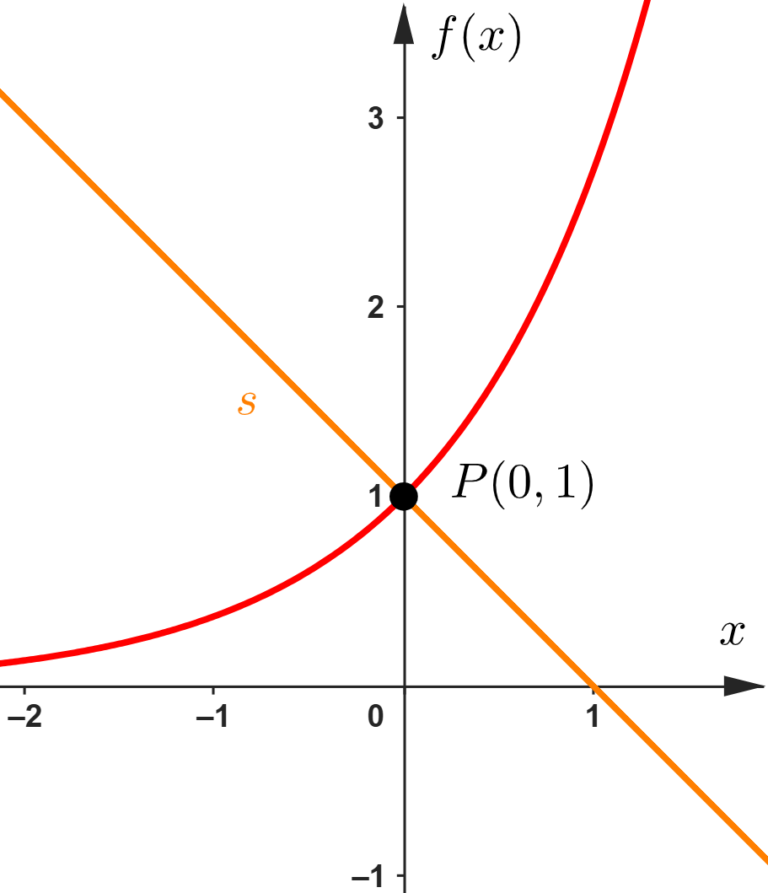
Mas afinal, como achamos a equação da reta normal? Utilizaremos de uma informação que disse anteriormente, que a reta normal é perpendicular à reta tangente, e por causa disso, o coeficiente de uma é o inverso oposto da outra.
Não entendeu nada do que eu disse, não é? Vamos passo a passo, se eu tenho um número
Chamando então o coeficiente angular da reta tangente de
Sabendo que a equação da reta normal tem a seguinte forma:
Podemos reescrever o coeficiente angular da reta normal (
Isso irá nos ser útil, porque sabemos encontrar o coeficiente da reta tangente, ele é igual à derivada da função no ponto
Substituindo na equação da reta
Por fim, encontramos a equação da reta normal à curva da função
Para fechar com chave de ouro, que tal representarmos as duas retas no gráfico?