Eis que você começa a faculdade de engenharia e se depara com uma matéria chamada “Cálculo”, muito provavelmente o primeiro assunto que irás estudar é limites, um conteúdo que causa dor de cabeça em muitos, mas não é nada de outro mundo, como tentarei mostrar nesse artigo.
O que é um limite?
É importantíssimo que saibas bem o que é uma função para que possas entender o conceito de limite. Há algumas funções que possuem restrições em seus domínios, ou seja, para determinados valores de $x$ (variável independente), ao substituirmos na função, chegamos em uma indeterminação matemática (situação em que é impossível obter um resultado). E para sinalizar o valor onde não há função, utilizamos uma bolinha aberta (não pintada) no gráfico:
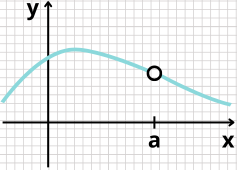
A nível de médio, essa informação e constatação já nos seria suficiente, mas em cursos superiores de exatas, utilizamos o artifício matemático chamado “Limite”, para saber o que acontece com a função quando $x$ se aproxima desse valor que não pertence ao domínio da função, em outras palavras, analisamos o que acontece com a função para valores muito próximos da bolinha aberta. A notação do limite de uma função qualquer é descrita pela seguinte simbologia:
$$\displaystyle \lim_{x\to a} f(x) = L$$
Podemos ler essa expressão assim: “Limite da função $f(x)$, para $x$ tendendo à $a$ é igual a um valor L”. Traduzindo do matematiquês para o bom e velho português, o limite de $f(x)$ (valor ao qual a função se aproxima) para $x$ se aproximando de um valor $a$ (um número ou letra qualquer) é igual a um determinado valor $L$ (assim como $a$, pode ser qualquer valor).
Exemplo: Calcule o limite da função abaixo, quando $x$ tender à $2$
$$f(x)=\frac{x^2-4}{x-2}$$
Antes de calcularmos esse tal de limite, vamos dar uma olhada na função, o que acontecerá se substituirmos $2$ pela variável $x$?
$$f(x)=\frac{x^2-4}{x-2}$$
$$f(2)=\frac{2^2-4}{2-2}$$
$$f(2)=\frac{4-4}{0}$$
$$f(2)=\frac{0}{0}$$
Chegamos em uma indeterminação, pois não é possível resolver uma divisão de zero por zero, portanto, $x=2$ não está no nosso domínio, e como já foi falado no artigo, marcamos no gráfico da função essa indeterminação como uma bolinha aberta
Ou seja, não há função nesse ponto, mas o que acontece com o $f(x)$ à medida que o $x$ se aproxima de $2$? É para responder isso que calculamos o limite de uma função. Primeiramente, vamos montar a expressão do limite:
$$\displaystyle \lim_{x\to2}\frac{x^2-4}{x-2}$$
Para calcular o limite, basta substituirmos o valor para o qual $x$ está tendendo na função
$$\displaystyle \lim_{x\to2}\frac{x^2-4}{x-2}=\frac{2^2-4}{2-2}=\frac{0}{0}$$
Assim como antes, chegamos em um impasse, no entanto, quando estamos calculando o limite de uma função, podemos fazer manipulações de forma a simplificarmos a expressão e eliminarmos a indeterminação, coisa que não poderíamos fazer normalmente. Intuitivamente, podemos concluir que quem está causando a indeterminação é o termo $x-2$, pois o denominador resulta em zero justamente quando substituímos o $2$ nesse termo, então, de alguma forma devemos eliminá-lo para podermos calcular o limite. Irei fatorar o numerador, e logo você entenderá o porquê fiz isso
$$\displaystyle \lim_{x\to2}\frac{x^2-4}{x-2}= \displaystyle \lim_{x\to2}\frac{(x+2)(x-2)}{x-2}$$
Olha só quem apareceu no numerador, $x-2$, uma vez que temos esse termo no numerador e denominador, podemos simplificá-los. Mas antes, um detalhe importante: Enquanto estivermos manipulando a expressão, temos que escrever a notação do limite ($\displaystyle \lim_{x\to a}$), caso não façamos isso, estaremos cometendo um erro matemático e muitos professores penalizam o aluno por isso, mesmo que o cálculo esteja correto.
$$\displaystyle \lim_{x\to2}\frac{(x+2)(x-2)}{x-2}=\displaystyle \lim_{x\to2}x+2$$
Agora, substituímos novamente o valor que $x$ está se aproximando (ao fazermos isso, podemos parar de escrever a notação do limite)
$$\displaystyle \lim_{x\to2}x+2=2+2=4$$
Descobrimos por meio desse cálculo, que à medida que o $x$ se aproxima de $2$, nossa função, $f(x)$, se aproxima de $4$, como podemos constatar no próprio gráfico da função:
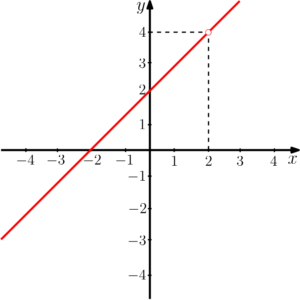
Como os gráficos de algumas funções são complexos, resolver os limites nos ajuda a calcular o que não podemos visualizar graficamente.
Limites laterais
Existe um conceito extremamente importante, chamado “limites laterais”, que nos ajudam a calcular o(s) limite(s) de uma função ao olharmos o gráfico dela. Para que exista limite para uma função em um determinado valor de $x$, os limites laterais devem ser iguais, em outras palavras, o valor que $f(x)$ se aproxima quando $x$ tende a um valor $a$ pelo lado esquerdo (levando em conta um número muito próximo de $a$, mas menor que $a$), deve ser igual ao valor que $f(x)$ se aproxima quando $x$ tende a esse mesmo $a$ pelo lado direito (um valor bem próximo de $a$, mas maior que $a$). Formalizando o que foi dito em termos matemáticos:
$$\displaystyle\lim_{x\to a^-}f(x)=\displaystyle\lim_{x\to a^+}f(x)=\displaystyle\lim_{x\to a}f(x)=L$$
O limite lateral pela esquerda é representado com um sinal de negativo no expoente do $a$ ($-$), já o pelo lado direito tem um sinal de positivo ($+$). Caso um dos limites laterais for diferente, significa que para aquele valor $a$ que o $x$ se aproxima, não existe limite
$$\displaystyle\lim_{x\to a^-}f(x)\neq\displaystyle\lim_{x\to a^+}f(x) ;\;\displaystyle\lim_{x\to a}f(x)=\not\exists$$
É um pouco complicado esse conceito, eu sei, mas vamos resolver um exercício para entendermos melhor
Exemplo: Calcule os limites da função cujo gráfico está representado abaixo:
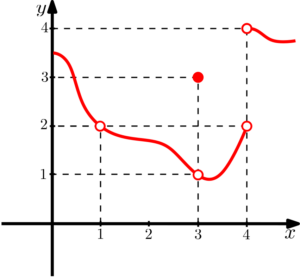
a) $\displaystyle\lim_{x\to1^-}f(x)$
b) $\displaystyle\lim_{x\to1^+}f(x)$
c) $\displaystyle\lim_{x\to1}f(x)$
d) $\displaystyle\lim_{x\to3^-}f(x)$
e) $\displaystyle\lim_{x\to3^+}f(x)$
f) $\displaystyle\lim_{x\to3}f(x)$
g) $\displaystyle\lim_{x\to4^-}f(x)$
h) $\displaystyle\lim_{x\to4^+}f(x)$
i) $\displaystyle\lim_{x\to4}f(x)$
Vamos lá, comecemos pelo limite lateral pela esquerda para $x$ tendendo à $1$. Olhando para o gráfico, quando $x$ vai se aproximando de $1$ pelo lado esquerdo, nossa função se aproxima de $2$, ou seja, ela tende à $2$, portanto:
$$\displaystyle\lim_{x\to1^-}f(x)=2$$
E observando da direita para a esquerda, a medida que o $x$ se aproxima de $1$ pelo lado direito, $f(x)$ se aproxima de $2$:
$$\displaystyle\lim_{x\to1^+}f(x)=2$$
Se os limites laterais para $x$ tendendo à $1$ são iguais, então, existe limite para esse ponto e ele é igual aos limites laterais, traduzindo para o matematiquês:
$$\displaystyle\lim_{x\to1}f(x)=2$$
As letras $d)$ e $e)$ podem causar certa confusão, pois quando olhamos para o gráfico, temos uma bolinha pintada (fechada, desenhada) para $x=3$, e isso só está lá para nos atrapalhar, pois indica apenas que há função para $x=3$ e que vale $3$, portanto, $f(3)=3$. Para os limites, nos interessa apenas o que está acontecendo “ao redor” desse valor, ou seja, quando $x$ está se aproximando de $3$, não quando $x$ é exatamente igual à $3$. Podemos constatar então, que ambos os limites laterais para $x$ tendendo à $3$ são iguais, resultando em $1$, e concluímos com isso, que existe limite nesse ponto e vale também $1$
$$\displaystyle\lim_{x\to 3^-}f(x)= \displaystyle\lim_{x\to 3^+}f(x)=\displaystyle\lim_{x\to a}f(x)=1$$
Agora iremos observar os limites laterais para $x$ tendendo à $4$, nesse caso acontece algo interessante, quando $x$ tende a $4$ pelo lado esquerdo do gráfico, $f(x)$ tende à $2$
$$\displaystyle\lim_{x\to4^-}f(x)=2$$
Já quando olhamos da direita para a esquerda, percebemos que $f(x)$ se aproxima de $4$, à medida que $x$ tende à $4$
$$\displaystyle\lim_{x\to4^+}f(x)=4$$
O que faremos? O limite da função é $2$ ou é $4$? Nenhum dos dois valores, lembra o que eu disse anteriormente? Para que haja limite quando $x$ se aproxima a um determinado valor $a$, os limites laterais devem ser iguais, caso contrário, não existe limite para $x$ tendendo à $a$
$$\displaystyle\lim_{x\to 4^-}f(x)\neq\displaystyle\lim_{x\to 4^+}f(x) ;\;\displaystyle\lim_{x\to 4}f(x)=\not\exists$$
Como calcular um limite algébrico?
Por mais que a principal utilidade do limite seja para analisar o que acontece em indeterminações e descontinuidades de funções, podemos calcular o limite de funções para qualquer ponto, muitas vezes seu valor vai ser o mesmo que o da função, mas não há problema nisso.
Exemplo 1: Calcule o limite abaixo
$$\displaystyle\lim_{x\to -1}x^2+3x+4$$
Para calcular o limite não tem segredo, é só substituirmos o valor para o qual $x$ está tendendo na função
$$\displaystyle\lim_{x\to -1}x^2+3x+4=(-1)^2+3.(-1)+4=1-3+4=2$$
Simples não? Infelizmente, é certo dizer que dificilmente cairá uma questão dessa na sua prova de cálculo, esse tipo de questão só é abordado na hora que os alunos são apresentados ao conceito de limites (fiz diferente nesse artigo, pois achei pertinente)
Exemplo 2: Calcule o limite abaixo
$$\displaystyle\lim_{t\to3^+}=\frac{t^2-1}{t-3}$$
Tudo o que aprendemos utilizando $x$, funciona para outra letra, então não se preocupe com esse $t$. Para resolvermos, substituímos o valor que $t$ está tendendo onde tem $t$ na expressão
$$\displaystyle\lim_{t\to3^+}=\frac{t^2-1}{t-3}=\frac{3^2-1}{3-3}=\frac{9-1}{0}=\frac{8}{0}$$
Chegamos em uma indeterminação, certo? De fato, normalmente, quando chegamos em uma divisão por zero, paramos a conta e escrevemos que não existe resposta, mas ao calcularmos limites, uma divisão por zero não é um problema, pois aquele “zero” ali não é exatamente zero, é um valor muito próximo de zero, tão pequeno, tão pequeno, que tende à zero, mas não é zero, e isso se dá pelo fato de termos substituído um valor que se aproxima de $3$ (mas que não é $3$). Como resolvemos então? Utilizaremos uma noção adquirida na divisão, tomemos por exemplo a seguinte divisão:
$$\frac{100}{10}=10$$
Se ao invés de dividirmos $100$ por $100$, dividíssemos por $4$?
$$\frac{100}{4}=25$$
O resultado da divisão aumentou de $10$ para $25$. E por $2$?
$$\frac{100}{2}=50$$
Aumentou ainda mais, então, por lógica, à medida que diminuímos o valor que divide outro número (e uma fração indica divisão), o resultado vai aumentando. Portanto, se o valor do denominador (quem divide) for tão pequeno, a ponto de se aproximar de zero, podemos deduzir que o resultado dessa divisão vai ser um valor tão grande, tão grande, que tenderá a infinito
$$\displaystyle\lim_{t\to3^+}=\frac{8}{0}=\infty$$
Não esqueça dessa informação, pois será muito importante para você não travar em certas questões de limites. O que dificulta nossa vida na resolução de limites é quando há alguma indeterminação, como vemos antes no caso da função $f(x)=\dfrac{x^2-4}{x-2}$, onde precisamos realizar alguma manipulação algébrica para eliminar a indeterminação e assim resolver o limite.
Limites indeterminados
Há vários tipos de indeterminação, citarei aqui os principais e falarei superficialmente como resolver cada caso, farei dessa forma para que o artigo não fique desnecessariamente grande e enfadonho.
Zero sobre zero:
Quando estamos resolvendo um limite e chegamos em zero dividido por zero, geralmente utilizamos produtos notáveis, fatoração e/ou divisão de polinômios para eliminarmos a indeterminação.
Exemplo: Resolva o limite abaixo
$$\displaystyle\lim_{x\to1}\frac{x^2-3x+2}{x-1}$$
Com a prática, você irá perceber se há indeterminação na maioria dos limites, mas é aconselhável que verifique substituindo o valor que $x$ tende na função, pois alguns professores exigem que você demonstre que se trata de um limite indeterminado
$$\displaystyle\lim_{x\to1}\frac{x^2-3x+2}{x-1}=\frac{1^2-3.1+2}{1-1}=\frac{1-3+2}{0}=\frac{0}{0}$$
Está indeterminado, portanto, precisamos eliminar a indeterminação para resolvermos o limite. Nesse caso, quem está nos trazendo problema é o $x-1$, pois ao substituirmos $1$ nesse termo, chegamos em zero no denominador, e já que o numerador dá zero também, resulta na indeterminação. Vamos fatorar o numerador para fazermos surgir $x-1$ no numerador para simplificar ele como o que está no denominador. Irei utilizar a fatoração por Bhaskara (tem artigo sobre fatoração aqui no blog, confere lá):
$$x^2-3x+2$$
$$a=1,\;b=-3,\;c=2$$
$$x=\frac{-b\pm\sqrt{\Delta}}{2a}$$
$$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$$
$$x=\frac{-(-3)\pm\sqrt{(-3)^2-4.1.2}}{2.1}$$
$$x=\frac{3\pm\sqrt{9-8}}{2}$$
$$x=\frac{3\pm\sqrt{1}}{2}$$
$$x=\frac{3\pm1}{2}$$
$$x_1=\frac{3+1}{2}=\frac{4}{2}=2$$
$$x_2=\frac{3-1}{2}=\frac{2}{2}=1$$
Então, podemos reescrever o polinômio $$x^2-3x+2$$ da seguinte forma:
$$x^2-3x+2=(x-2)(x-1)$$
Fizemos aparecer o $x-1$, nos resta só então a resolução do limite
$$\displaystyle\lim_{x\to1}\frac{x^2-3x+2}{x-1}=\displaystyle\lim_{x\to1}\frac{(x-2)(x-1)}{x-1}=\displaystyle\lim_{x\to1}x-2$$
Por fim, conferimos se a indeterminação foi eliminada substituindo o valor para o qual $x$ tende na função
$$\displaystyle\lim_{x\to1}x-2=1-2=-1$$
Poderíamos resolver essa questão de uma outra forma, utilizando um dispositivo chamado Briot Ruffini (terá um artigo só sobre ele futuramente), que consiste em um método de divisão de polinômios, que facilita a obtenção do termo que causa a indeterminação no limite.
Infinito sobre infinito:
Uma das maravilhosas coisas que os limites nos permitem fazer, é determinar o que acontece com uma função quando a variável tende a um valor infinito (seja ele positivo ou negativo), para isso, montamos a seguinte expressão:
$$\displaystyle\lim_{x\to\infty}f(x)$$
Ou então:
$$\displaystyle\lim_{x\to -\infty}f(x)$$
Exemplo 1: Resolva o limite abaixo
$$\displaystyle\lim_{x\to\infty}x^2-20$$
Faremos o mesmo que fizemos até agora, substituiremos o valor que $x$ se aproxima onde tiver $x$ na expressão matemática
$$\displaystyle\lim_{x\to\infty}x^2-20=(\infty)^2-20$$
Infinito elevado ao quadrado, continua sendo infinito, portanto:
$$(\infty)^2-20=\infty-20$$
Subtrair $20$ unidades de um valor infinito, não o altera em nada, então podemos continuar considerando como infinito o resultado dessa subtração
$$\infty-20=\infty$$
Portanto,
$$\displaystyle\lim_{x\to\infty}x^2-20=\infty$$
Isso significa que quando $x$ crescer a ponto de se aproximar de um valor infinito, nossa função $x^2-20$ também tenderá a infinito
Exemplo 2: Resolva o limite abaixo
$$\displaystyle\lim_{x\to\infty}\frac{2}{\sqrt{x}+5}$$
Vamos começar a resolver para ver o que acontece
$$\displaystyle\lim_{x\to\infty}\frac{2}{\sqrt{x}+5}=\frac{2}{\sqrt{\infty}+5}=\frac{2}{\infty+5}=\frac{2}{\infty}$$
Qual o resultado dessa divisão? Utilizaremos lógica para achá-lo. Suponhamos que dividiremos uma pizza normal (tamanho M) em pedaços iguais para $4$ pessoas, cada uma ficará com $1$ pedaço que corresponderá a um quarto dessa pizza, e se eu dividir para $8$ pessoas? Cada uma ficará com um pedaço, mas que será menor do que aquelas primeiras $4$ pessoas receberam, e se eu tentasse dividir uma pizza para $2$ milhões de pessoas, cada um receberia praticamente um pedaço do tamanho de um grão de areia. Agora pensemos naquela divisão, ao dividirmos $2$ por um valor tão grande, tão grande que se aproxima a infinito, teremos como resultado um valor tão pequeno, tão pequeno, que se aproxima de zero.
$$\displaystyle\lim_{x\to\infty}\frac{2}{\sqrt{x}+5}=\frac{2}{\infty}=0$$
Um detalhe importante a ser considerado, é que esse valor que se aproxima de zero é positivo, pois tanto o $2$, quanto o infinito tinham sinais positivos, e pela análise de sinais, o resultado disso é um valor positivo. Devemos sempre analisar os sinais em exercícios assim, porque caso o numerador fosse negativo, o resultado seria um número bem próximo de zero, só que negativo (para alguns exercícios essa explicação é necessária para justificar a resposta).
Em algumas situações, podemos chegar em infinito sobre infinito, que é uma indeterminação, pois por mais que pareça contraditório, há infinitos maiores que outros, e “infinito” não é um número específico, é um conceito que é utilizado quando temos valores incomensuráveis (que não conseguimos medir de tão grandes), tudo isso faz com que seja impossível determinar o resultado da divisão de um infinito por outro. Para resolver esse tipo de indeterminação, basta eliminarmos a variável de maior grau que os polinômios do numerador e denominador tiverem em comum.
Exemplo 3: Calcule o limite abaixo:
$$\displaystyle\lim_{x\to\infty}\frac{x^3-2}{ x^2+2x+1}$$
Comecemos a resolver
$$\displaystyle\lim_{x\to\infty}\frac{x^3-2}{ x^2+2x+1}=\frac{(\infty)^3-2}{(\infty)^2+2.\infty+1}=\frac{\infty}{\infty}$$
Para limites com indeterminação infinito sobre infinito, só nos interessa os termos de maior grau para eliminarmos a indeterminação, então, podemos reescrever ao limite da seguinte maneira:
$$\displaystyle\lim_{x\to\infty}\frac{x^3}{x^2}$$
Podemos simplificar os termos utilizando a propriedade da divisão de potências de mesma base
$$\displaystyle\lim_{x\to\infty}\frac{x^3}{x^2}=\displaystyle\lim_{x\to\infty}x^{3-2}=\displaystyle\lim_{x\to\infty}x$$
Uma vez que eliminamos o $x$ do denominador, não chegaremos em infinito sobre infinito, nos restando apenas finalizar o cálculo
$$\displaystyle\lim_{x\to\infty}x=\infty;\;\displaystyle\lim_{x\to\infty}\frac{x^3-2}{x^2+2x+1}=\infty$$
Tipos específicos de limites
Há alguns tipos de limites, que exigem métodos específicos para se resolver, irei mencionar a solução e mostrar a aparência deles.
Limites modulares:
Limites que tiverem o dispositivo “módulo”, devem ser resolvidos utilizando os conceitos sobre a aplicação do módulo, pois ele altera o valor que estiver dentro dele para garantir que o resultado seja sempre positivo.
Exemplos de limites modulares:
1) $\displaystyle\lim_{x\to2}|x|$
2) $\displaystyle\lim_{x\to3}\frac{|x^2-9|}{x-3}$
3) $\displaystyle\lim_{x\to1}\frac{x^2+2x-3}{|x-1|}$
Limites fundamentais:
Os limites fundamentais, são determinados tipos de limites, trigonométricos (que possuem funções trigonométricas, como seno e cosseno) ou exponenciais, que conseguimos resolver utilizando uma ou mais das relações abaixo:
Primeira relação:
$$\displaystyle\lim_{x\to0}\frac{sen(x)}{x}=1$$
Segunda relação:
$$\displaystyle\lim_{x\to0}\frac{1-cos(x)}{x}=0$$
Terceira relação:
$$\displaystyle\lim_{x\to0}\frac{tan(x)}{x}=1$$
Quarta relação:
$$\displaystyle\lim_{x\to\pm\infty}\left(1+\frac{1}{x}\right)^x=e$$
Quinta relação:
$$\displaystyle\lim_{x\to0}\frac{a^x-1}{x}=\ln(a)$$
Sexta relação:
$$\displaystyle\lim_{x\to\pm\infty}\left(1+x\right)^{\frac{1}{x}}=e$$
Exemplos de limites fundamentais:
1) $\displaystyle\lim_{x\to0}\frac{sen(4x)}{4x}$
2) $\displaystyle\lim_{x\to\pm\infty}\left(1+\frac{1}{x}\right)^{5x}$
3) $\displaystyle\lim_{x\to0}\frac{3^x-1}{x}$
Conceitos relevantes dos limites
É possível determinar algumas informações de funções utilizando os limites, como descobrir se a função é descontínua em determinado ponto e encontrar o limite de uma função qualquer com base em outras duas conhecidas. Discorrerei sobre eles sucintamente (de forma resumida), pois cada um merece um artigo próprio, tamanha utilidade que esses possuem.
Teorema do confronto:
O Teorema do Confronto, ou Teorema do Sanduíche, afirma que se uma função está “espremida” entre duas outras funções que têm o mesmo limite em um ponto, então a função intermediária também deve ter esse limite. É particularmente útil quando a função não pode ser facilmente avaliada diretamente, ou quando não conhecemos sua lei de formação (expressão ou “corpo” da função). Podemos descrever isso com a seguinte sentença matemática:
Se,
$$g(x)\leq f(x)\leq h(x)$$
E,
$$\displaystyle\lim_{x\to a}g(x)=\displaystyle\lim_{x\to a}h(x)=L$$
Então,
$$\displaystyle\lim_{x\to a}f(x)=L$$
Continuidade:
Os limites são fundamentais para definir a continuidade de uma função em um ponto. Uma função é contínua em um ponto se o limite da função, enquanto se aproxima desse ponto, é igual ao valor da função no ponto, ou seja, $f(x)$ é contínua para $x=a$ se:
$$f(a)=\displaystyle\lim_{x\to a}f(x)$$
Assíntotas:
Assíntotas descrevem o comportamento de funções à medida que se aproximam de pontos ou linhas específicas (imaginárias), que representam uma descontinuidade de ou a convergência do gráfico para um valor finito. Utilizamos os limites para determinar se existem e quais são as assíntotas horizontais, verticais e oblíquas de uma função, colaborando para entender o comportamento delas.
Exercícios resolvidos de limites
1. Calcule o limite abaixo
$$\displaystyle\lim_{x\to 0}\frac{x^3}{x^2+2x}$$
Primeiramente, substituímos o valor para o qual $x$ está tendendo onde tiver $x$ para verificar se há indeterminação
$$\displaystyle\lim_{x\to 0}\frac{x^3}{x^2+2x}=\frac{0^3}{0^2+2.0}=\frac{0}{0}$$
Indeterminado, para calcular o limite, precisamos eliminar essa indeterminação, mas quem poderia estar ocasionando isso? O próprio $x$, pois ao substituirmos ele por zero, zeramos numerador e denominador, então, vamos colocá-lo em evidência e simplificá-lo
$$\displaystyle\lim_{x\to 0}\frac{x^3}{x^2+2x}=\displaystyle\lim_{x\to 0}\frac{x^3}{x(x+2)}=\displaystyle\lim_{x\to 0}\frac{x^2}{x+2}$$
Agora, vamos substituir $x$ por zero novamente e vermos se solucionamos o problema
$$\displaystyle\lim_{x\to 0}\frac{x^2}{x+2}=\frac{0^2}{0+2}=\frac{0}{2}=0$$
2. Resolva o limite abaixo
$$\displaystyle\lim_{x\to -3}\frac{x^2+6x+9}{x^2-9}$$
Como antes, verificamos se há indeterminação
$$\displaystyle\lim_{x\to -3}\frac{(-3)^2+6.(-3)+9}{(-3)^2-9}=\frac{9-18+9}{9-9}=\frac{0}{0}$$
Para quem chegou até aqui, irei dar uma dica valiosíssima para resolver limites polinomiais (que têm polinômios se dividindo), o termo responsável pela indeterminação será sempre, sempre, $x$ e o valor oposto ao qual ele está tendendo, nessa questão o $x$ está tendendo à $-3$, então, precisamos eliminar o termo $x+3$ para acabarmos com a indeterminação. Farei aparecer esse termo fatorando os polinômios (é indispensável dominar a matemática básica para entender e resolver limites)
$$\displaystyle\lim_{x\to -3}\frac{x^2+6x+9}{x^2-9}=\displaystyle\lim_{x\to -3}\frac{(x+3)(x+3)}{(x+3)(x-3)}=\displaystyle\lim_{x\to -3}\frac{x+3}{x-3}$$
Uma vez eliminado o termo problemático, vamos resolver o limite
$$\displaystyle\lim_{x\to -3}\frac{x+3}{x-3}=\frac{-3+3}{-3-3}=\frac{0}{-6}=0$$
3. Calcule, se existir, o limite para $x\rightarrow2$ da função abaixo:
$$f(x)=\begin{cases}x^2+4;\; se\;x<2\\x^3;\;se\;x\geq2\end{cases}$$
Antes de você abandonar o artigo ao se deparar com a expressão acima, respire, e vamos passo a passo destrinchá-la. O que essa sentença quer dizer é que a função $f(x)$ vai assumir o comportamento descrito pela expressão $x^2+4$ para valores de $x$ menores que $2$ e para valores maiores ou iguais a $2$, ela se comportará como $x^3$. Para calcular o limite de uma função como essa, utilizaremos o conceito de limites laterais, se eles forem iguais, significa que a função possui limite para $x$ tendendo à $2$
$$\displaystyle\lim_{x\to2^-}x^2+4=2^2+4=8$$
O limite lateral tendendo pelo lado esquerdo representa um valor muito próximo de $2$, e menor que $2$, por isso utilizei a expressão acima. Para calcular o outro limite lateral, devemos utilizar $x^3$
$$\displaystyle\lim_{x\to2^+}x^3=2^3=8$$
Os limites laterais são iguais, portanto,
$$\displaystyle\lim_{x\to2}f(x)=8$$
Formado em Eletrotécnica pelo IFRN, além de ter cursos de Matemática Básica e Cálculo pela empresa Help Engenharia.
