Graças a sua característica principal, a função logarítmica permite analisar situações em que há várias multiplicações envolvidas, como juros compostos e modelos populacionais que levam em conta múltiplos fatores, podendo ser usada até para analisar um terremoto e determinar sua magnitude. Muito parecida com a função exponencial, ela pode ser tão útil e interessante quanto.
O que é uma função logarítmica?
Ela é uma função que possui um logaritmo, e cuja variável (letra) está em seu logaritmando.
Exemplos:
1) $log_{3}x$
2) $log_{\frac{1}{5}}x$
3) $ln(x)$
Sua forma geral é:
$$f(x)=log_{b}x$$
A base do logaritmo ($b$) deve ser maior que zero e diferente de $1$, e no logaritmando só são admitidos números positivos maiores que zero. Por esse motivo, o domínio (valores possíveis para a variável independente, nesse caso o $x$) é restrito aos números reais positivos, sem incluir o zero. Já o contradomínio da função não possui restrição, portanto, inclui todo o conjunto dos números reais.
Gráfico da função logarítmica
Há duas possibilidades de gráfico para a função logarítmica, o primeiro é um gráfico à direita do eixo $f(x)$ (eixo $y$), ou seja, para valores positivos de $x$, e assim como a função exponencial, há dois tipos de formatos para o gráfico da função logarítmica, o primeiro consiste em uma curva crescente que começa com valores próximos a zero, abaixo do eixo horizontal (eixo $x$) e vai crescendo de forma acentuada depois de intersectá-lo
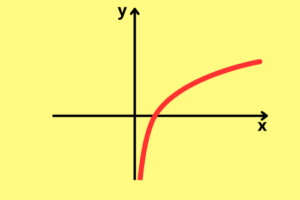
O segundo possui comportamento contrário ao anterior, começando com valores muito pequenos a medida, e crescendo de forma gradual ao se aproximar do eixo $x$ pela parte de cima do eixo $y$ e após cortar o eixo horizontal, começa a crescer rapidamente
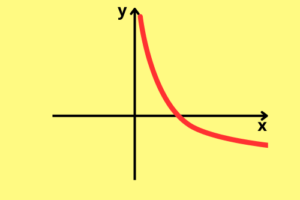
O que irá determinar se a função resultará em um ou outro é a base do log, se ela for maior que $1$, teremos o primeiro caso, crescente de baixo para cima, e se tiver valor entre $0$ e $1$, será decrescente, nesse mesmo sentido. A segunda possibilidade de gráfico é quando temos $-x$ no logaritmando do log, fazendo com que o gráfico fique à esquerda do eixo $f(x)$, podendo ter os mesmos comportamentos, só que de forma “espelhada”.
Gráfico da função $f(x)=log_2{}-x$:
Como fazer o gráfico da função logarítmica?
As funções logarítmicas que estiverem em sua forma padrão ($f(x)=log_{b}x$) intersectarão o eixo $x$ em $x=1$, pois para acharmos onde o gráfico toca no eixo horizontal, zeramos o valor de $f(x)$, e ao isolarmos o $x$, sempre teremos $1$ como resultado, portanto, independentemente do valor da base, o gráfico irá intersectar o eixo das abscissas em $(1,0)$. Vale ressaltar que o gráfico nunca irá tocar o eixo $y$.
Para descobrirmos os valores de $f(x)$, escolheremos para $x$ números que resultem em valores inteiros ao resolver o logaritmo, tomemos como exemplo a função abaixo
$$f(x)=log_{2}x$$
O gráfico será crescente, pois a base é maior que $1$, mas além disso, os valores que ao substitui-los no lugar de $x$ resultarão em números inteiros, serão potências de $2$ e seus inversos:
$$f(x)=log_{2}x$$
1)
$$f(2)=log_{2}2=1$$
2)
$$f(4)=log_{2}4=2$$
3)
$$f(8)=log_{2}8=3$$
4)
$$f(\frac{1}{2})=log_{2}\frac{1}{2}=-1$$
5)
$$f(\frac{1}{4})=log_{2}\frac{1}{4}=-2$$
6)
$$f(\frac{1}{8})=log_{2}\frac{1}{8}=-3$$
Não é necessário selecionar tantos pontos assim, basta pegar umas três potências e o resto do gráfico será um prolongamento disso
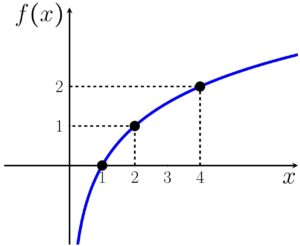
Se a base for um valor entre $0$ e $1$, o processo será o mesmo, a única coisa que mudará é que o gráfico será decrescente, ou seja, à medida que o valor de $x$ aumenta, o $f(x)$ diminui
Exemplo:
Determine o gráfico da função $f(x)=log_{\frac{1}{3}}x$
Um dividido por três dá aproximadamente $0,33$, portanto, o gráfico terá uma curva decrescente. E pegaremos algumas potências de base $3$ para montarmos os primeiros pontos no gráfico. Dica: Escolha potências de base inteira, como $3$, $9$, $27$, pois independentemente se o gráfico é crescente ou decrescente, ao mesmo tempo que o $x$ aumenta, o $f(x)$ irá crescer ou decrescer de forma acentuada após a intersecção do gráfico com o eixo $x$
$$f(x)=log_{\frac{1}{3}}x$$
1)
$$f(3)=log_{\frac{1}{3}}3=-1$$
2)
$$f(9)=log_{\frac{1}{3}}9=-2$$
3)
$$f(27)=log_{\frac{1}{3}}27=-3$$
Agora podemos esboçar o gráfico
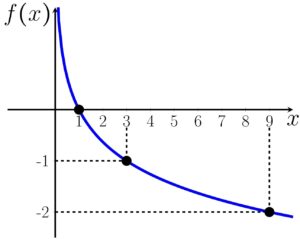
Aconselho fortemente que você leia o nosso artigo sobre logaritmo e que estude sobre as potências, para que tenha pleno entendimento do porquê de escolhermos esses valores para substituir na variável independente.
Relação entre a função logarítmica e a função exponencial
Toda semelhança entre a função logarítmica e a função exponencial não é mera coincidência, pois uma é o inverso da outra, fatores que dão indícios disso é o domínio e contradomínio, o gráfico e a intersecção com um dos eixos.
Exercícios resolvidos de função logarítmica
1. Desenhe o gráfico da função $f(x)=ln(x)$
Esse é um famoso log, chamado “logaritmo natural”, presente em cálculos de diversos fenômenos da natureza, ele é o log na base $e$ (constante de Euler, valendo aproximadamente $2,718$). Para montarmos o gráfico faremos o mesmo processo, só que dessa vez as potências terão como base a constante $e$. Ah e não vamos esquecer que o gráfico será crescente, pois a base é maior que $1$
$$f(x)=ln(x)=log_{e}x$$
1)
$$f(e^1)=log_{e}e^1=1$$
2)
$$f(e^2)=log_{e}e^2=2$$
3)
$$f(e^3)=log_{e}e^3=3$$
Com essas informações, podemos plotar o gráfico aproximado
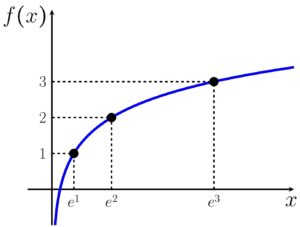
2. Calcule $f(4)$, para a função abaixo
$$f(x)=log_{4}\sqrt[3]{x}+log_{4}\sqrt[3]{4x}$$
Antes de substituirmos o valor de $x$ na função, vamos juntar esses logs em um único, para simplificarmos a expressão
$$f(x)=log_{4}\sqrt[3]{x}+log_{4}\sqrt[3]{4x}$$
$$f(x)=log_{4}\sqrt[3]{x.4x}$$
$$f(x)=log_{4}\sqrt[3]{4x^2}$$
Agora substituímos o valor de $x$
$$f(x)=log_{4}\sqrt[3]{4x^2}$$
$$f(4)=log_{4}\sqrt[3]{4.4^2}$$
$$f(4)=log_{4}\sqrt[3]{4.16}$$
$$f(4)=log_{4}\sqrt[3]{64}$$
$$f(4)=log_{4}4$$
$$f(4)=1$$
Formado em Eletrotécnica pelo IFRN, além de ter cursos de Matemática Básica e Cálculo pela empresa Help Engenharia.
