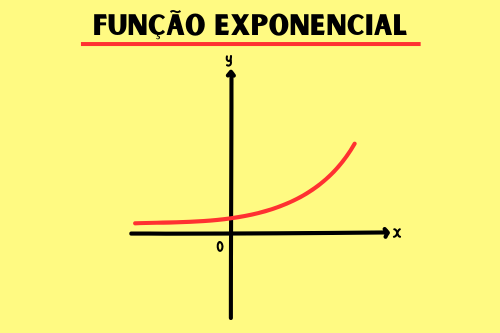
Onde há crescimento ou decrescimento de algo, a função exponencial estará presente, devido a suas características, ela é um ótimo modelo para se analisar o aumento populacional, taxa de juros e até mesmo a propagação de um vírus de acordo com o número de pessoas infectadas.
O que é uma função exponencial?
Ela é uma função que possui um exponencial, ou seja, uma constante elevada a uma letra (variável).
Exemplos:
1)
2)
3)
Sua forma geral é:
Onde
O sinal da variável que vai no expoente pode ser negativo, isso irá impactar única e exclusivamente o comportamento do gráfico da função, como veremos ao longo do artigo.
Gráfico da função exponencial
Há dois tipos de formatos para o gráfico da função exponencial, o primeiro e mais conhecido é o de uma curva que cresce infinitamente, iniciando com valores muito baixos de
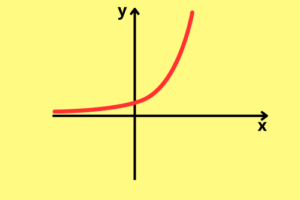
E o outro é uma curva que da esquerda para a direita parte de um valor muito alto de
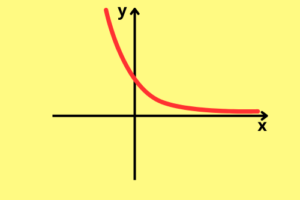
O que vai determinar se teremos a primeira ou a segunda situação é a base do exponencial, se ela for maior que
Como fazer o gráfico da função exponencial?
Todas as funções exponenciais “puras” (no formato
Se a função for crescente, o gráfico começará a aumentar bem devagar, e após intersectar o eixo vertical em
Exemplo:
Determine o gráfico da função
A base é maior que
1)
2)
3)
Agora montamos o gráfico, não será uma representação perfeita, mas será o suficiente para entendermos o comportamento da função
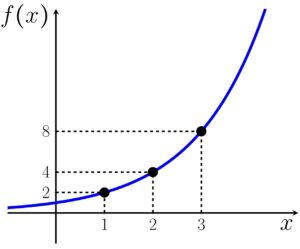
Uma consideração importante a ser feita é que a variável pode ter sinal negativo, isso não fará com que a função deixe de ser exponencial, só que o comportamento do gráfico em relação a base irá se inverter, ou seja, se
Exemplo:
Determine o gráfico da função
Normalmente, essa função resultaria em um gráfico crescente, pois a base é maior que zero, só que o expoente é negativo, ou seja, a curva do gráfico será decrescente. Nesse caso, vamos substituir os valores
1)
2)
3)
Então, podemos montar o gráfico aproximado
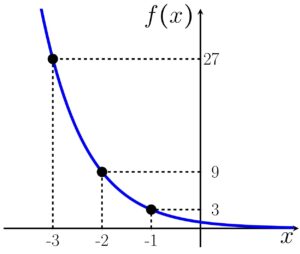
Podemos enxergar essa função de uma outra forma, para que fique fácil a visualização de o porquê ela é decrescente:
Fiz essa manipulação utilizando conhecimentos de potenciação. Implicitamente, a base possui um valor entre
Relação entre a função exponencial e a função logarítmica
Vale ressaltar que a função exponencial é a função inversa da função logarítmica, portanto, a maioria das características se comportam de maneira inversa, tomemos como exemplo o gráfico, que nunca intersecta o eixo
Exercícios resolvidos de função exponencial
1. Desenhe o gráfico da função
Primeiramente, de onde surgiu esse “
1)
2)
3)
Criamos então o gráfico da famosa função
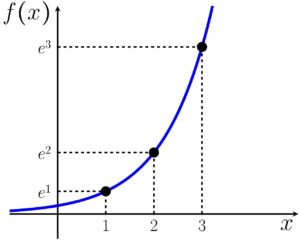
2. O crescimento de uma população de bactérias é dado pela função abaixo, onde
Quantas bactérias haverá após dois dias?
Basta substituirmos o número de dias no lugar de
Multiplicar por
Portanto, passados
3. O gráfico abaixo é de qual função?
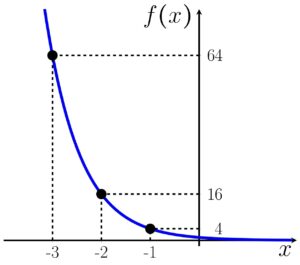
a)
b)
c)
d)
Como o gráfico é decrescente, não pode ser a letra A nem a B, agora nos resta analisar os pontos demarcados no gráfico para definirmos a função que gerou esse gráfico. Podemos substituir os valores de
Opa, já achamos nossa resposta, esse gráfico é da função que está na alternativa C. Outra forma que você poderia matar a questão é ao perceber que os números no eixo