Sendo a mais simples das funções polinomiais, e responsável por nos possibilitar a análise de coisas que crescem ou decrescem de forma uniforme, é indispensável estudá-la para entendermos o processo de criação do gráfico de uma função e suas aplicações.
O que é uma função de 1° grau?
Muitas vezes chamada de função afim ou função linear, ela é uma função, regra matemática que relaciona duas ou mais variáveis, que possui um polinômio de grau $1$, ou seja, o maior grau da variável é $1$.
Exemplos:
1) $f(x)=2x-3$
2) $f(x)=-x+1$
3) $f(x)=x$
Sua forma geral é dada por:
$$f(x)=ax+b$$
ou
$$y=ax+b$$
Onde $a$ e $b$ podem ser números quaisquer, geralmente pertencentes ao conjunto dos números reais (mas caso a questão especifique outro conjunto, consideraremos válidos apenas valores que pertençam a ele), e o $a$ deve ser diferente de zero, pois se o $a$ for igual à zero, teremos uma função constante.
Gráfico da função de 1° grau
O formato do gráfico da função linear é uma reta, que pode ser crescente ou decrescente, diferentemente do gráfico da função constante, cujo $f(x)$ não varia.
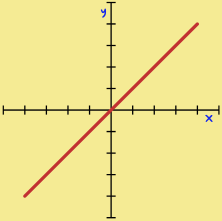
Como fazer o gráfico da função de 1° grau?
Para desenharmos o gráfico dessa função, precisamos apenas de dois pontos, mas quais devem ser eles? Podemos escolher alguns valores para $x$ e com o valor resultante da função marcamos dois pontos no plano cartesiano, mas há uma forma mais eficaz e que funcionará para toda e qualquer função afim. O método consiste em acharmos os pontos em que o gráfico intersecta os eixos $x$ e $y$, e podemos fazer isso ao zerarmos a variável dependente ou independente, vamos entender melhor por meio de um exemplo.
Exemplo:
Determine o gráfico da função $f(x)=2x-4$
Primeiramente, vamos zerar o $x$, para encontrarmos o valor em que o gráfico cruza o eixo $y$
$$f(x)=2x-4$$
$$f(0)=2.0-4$$
$$f(0)=0-4$$
$$f(0)=-4$$
Agora, zeramos o valor de $f(x)$ (ou $y$), para sabermos o valor em que o gráfico intersecta (toca) o eixo $x$, com a observação de que temos que isolar o $x$ nesse processo
$$f(x)=2x-4$$
$$0=2x-4$$
$$-2x=-4$$
$$x=\frac{-4}{-2}$$
$$x=2$$
Então, marcamos os pontos cujas coordenadas são $(0,-4)$ e $(2,0)$ no plano cartesiano e os ligamos
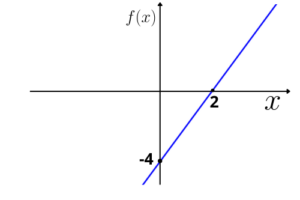
De forma geral, o valor que representa a intersecção do gráfico com o eixo $y$ é o coeficiente $b$, e podemos encontrar o ponto de toque com o outro eixo através da fórmula $-b/a$, utilizemos o exemplo acima para comprovar o que acabei de explicar
$$f(x)=2x-4$$
O coeficiente $b$, é o número que não estiver acompanhado da variável independente (nesse caso, o $x$), que na função em questão é $-4$, agora vamos usar a fórmula para descobrir onde o gráfico intersecta o eixo $x$
$$\frac{-b}{a}=\frac{-(-4)}{2}=\frac{4}{2}=2$$
Olha só, achamos os mesmos valores, só que de uma forma bem mais prática e rápida, e isso funciona para qualquer função linear. O único cuidado que você deve ter é de identificar corretamente os coeficientes $a$ e $b$, para isso, basta comparar a função dada na questão com a forma geral $f(x)=ax+b$.
Função de 1° grau crescente:
Quando a função tiver o coeficiente $a$ (quem multiplica a variável independente) positivo, ela será crescente, ou seja, à medida que o valor de $x$ aumentar, o valor de $f(x)$ também aumentará
Gráfico de uma função afim crescente:
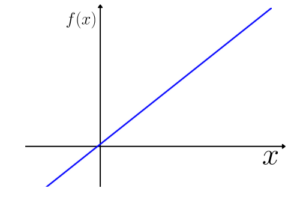
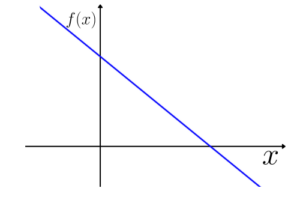
Função de 1° grau decrescente:
E quando o coeficiente $a$ for negativo, ela será decrescente, em outras palavras, à medida que o valor de $x$ aumentar, o valor de $f(x)$ diminuirá
Gráfico de uma função afim decrescente:
É importante ressaltar que o $a$ é chamado “coeficiente angular”, pois determina se a inclinação da função será positiva ou negativa (crescente ou negativa), e o $b$ é chamado “coeficiente linear” e como já foi explicado, determina o ponto de intersecção com o eixo $y$.
Aplicações da função de 1° grau
Sempre que possuirmos algo que cresce ou decresce de forma constante, dependendo de um outro valor, podemos utilizar a função de primeiro grau para representar graficamente essa situação.
Economia:
Podemos escrever a receita, lucro ou gasto total de uma transação financeira como uma função linear, desde que o valor de venda do produto seja constante.
Pesagem:
Podemos descrever o preço de determinado alimento aumentando ou diminuindo de acordo com o peso dele através de uma função afim.
Táxi:
Mesmo que já esteja em certo desuso por causa dos aplicativos de transporte, o táxi ainda é um meio de transporte muito usado e é um exemplo clássico de uso de função de 1° grau, pois o preço a pagar por uma viagem de táxi é dado por um valor fixo mais uma taxa de acordo com os quilômetros rodados.
Exercícios resolvidos de função de 1° grau
1. Determine o gráfico da função abaixo e seu valor para $x=3$
$$f(x)=x$$
Primeiramente, vamos substituir o valor de $x$ que é dado no enunciado para encontrarmos o valor de $f(x)$ correspondente
$$f(x)=x$$
$$f(3)=3$$
O valor de $f(x)$ é igual ao valor de $x$ e isso não é por acaso, essa função é uma velha conhecida da matemática, pois nela o valor da variável dependente será sempre igual ao valor da variável independente, e a ela é dada um nome especial: “Função identidade”. Agora vamos desenhar o gráfico dela, e bom, não temos nenhum número sozinho, isso significa que o gráfico não intersecta o eixo vertical? Não, pois podemos reescrever a função da seguinte forma (para facilitar a visualização)
$$f(x)=x+0$$
Quando não há nenhum valor aparente sem multiplicar a variável independente, significa que o coeficiente $b$ é igual à zero. E por fim, utilizaremos a fórmula citada anteriormente para achar o ponto de intersecção com o eixo horizontal, mas não vamos esquecer que $b=0$
$$\frac{-b}{a}=\frac{-0}{1}=0$$
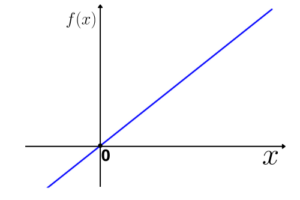
Portanto, o gráfico da função identidade será:
2. Um rapaz costuma emprestar $50$ reais a seus amigos, com a seguinte condição: para cada mês que não for devolvido o valor, será acrescentado mais $10$ ao valor inicial. Qual será a dívida após três meses sem pagar?
Através da modelagem matemática, vamos transformar essa situação em uma função. Temos um valor inicial ($50$ reais) que não muda, e um valor que varia de acordo com a passagem dos meses, então, podemos escrever a seguinte expressão:
$$D(t)=50+10t$$
Onde $D(t)$ é a dívida a ser paga, $t$ a quantidade de meses e o $10$ é o valor que será acrescentado à dívida a cada mês. Para calcular o montante a ser pago após três meses, basta substituir $3$ na variável que representa o tempo, na expressão acima
$$D(t)=50+10t$$
$$D(3)=50+10.3$$
$$D(3)=50+30$$
$$D(3)=80$$
Portanto, a pessoa que demorar três meses para devolver o dinheiro, terá que pagar $80$ reais, ou seja, trinta reais à mais do que os $50$ reais que foram emprestados.
