Praticamente tudo na física consiste em estudar e trabalhar com grandezas, dos mais diversos tipos e naturezas, sendo assim essencial entender o que elas são e como identificá-las de acordo com suas características.
O que é uma grandeza?
Em poucas palavras, uma grandeza é tudo o que conseguimos ou podemos medir, mensurar ou contar, independentemente do instrumento ou método que utilizamos para isso. E os exemplos de grandezas são infinitos, pois podemos medir desde o comprimento de um móvel, a profundidade de uma piscina, quantos litros há em uma garrafa, até o volume de areia que uma caçamba comporta, quantas estrelas há em um determinado sistema e a quantidade de pessoas que moram em uma cidade.
Exemplos de grandezas:
1) Tempo;
2) Comprimento;
3) Massa;
4) Velocidade;
5) Volume.
É importantíssimo mencionar que as grandezas possuem representações específicas chamadas Unidades de Medida, e elas nos ajudam a saber qual a natureza daquela grandeza, ou seja, qual tipo de fenômeno ou propriedade ela representa e o que ela indica. Há inúmeras unidades de medida, com várias grandezas possuindo mais de uma, e para definir um padrão afim de facilitar a comunicação e trabalho em escala mundial, foram determinadas pelo “Sistema Internacional de Unidades (SI)”, unidades de medida padrões para as grandezas mais importantes.
Exemplos de unidades de medida:
1) Metros [m] – Utilizado em grandezas que medem ou tem relação com comprimento;
2) Quilogramas [kg] – Utilizado em grandezas que envolvem peso ou massa de algo;
3) Segundos [s] – Utilizado na grandeza tempo ou grandezas que necessitam do tempo.
Tipos de grandezas
Há dois principais tipos de grandezas, as escalares e as vetoriais, saber diferenciá-las é essencial para entendermos o processo feito no cálculo envolvendo um ou outro tipo.
Grandezas escalares:
São as mais simples, que exigem que saibamos apenas seu valor numérico para que possamos manipulá-las e entender seu significado. Por exemplo: olhemos para a grandeza tempo, quando dizemos que “se passaram duas horas”, não é necessário dizer mais nada para entendermos quanto tempo se passou, da mesma forma, quando uma questão nos informa que um objeto tem massa igual à $80$ quilogramas, ela não dará informações adicionais como “são $80$ $kg$ para na vertical” ou ainda “tem massa de $80$ kg para a esquerda”, nos basta apenas saber o valor numérico para entendermos o dado que nos foi fornecido.
Exemplos de grandezas escalares:
1) Massa [$kg$ – quilograma];
2) Distância [$m$ – metro];
3) Tempo [$s$ – segundo];
4) Área [$m^2$ – metros quadrados];
5) Volume [$m^3$ – metros cúbicos];
6) Temperatura [$K$ – kelvin].
Grandezas vetoriais:
Diferentemente das escalares, as grandezas vetoriais necessitam de duas informações à mais do que apenas o valor numérico para que possamos entender o significado delas, é preciso sabermos a direção e sentido da grandeza.
Tomemos como exemplo a grandeza deslocamento, caso uma questão tenha em seu enunciado “um carro se deslocou”, nos falta informação, pois o carro pode ter se deslocado para esquerda, para direita, se a pista for plana ele terá se deslocado horizontalmente, no entanto, caso haja uma inclinação, ele deslocará verticalmente, dependendo da questão isso será essencial para a resolvermos. E caso tenha dúvidas sobre direção e sentido, a diferença entre eles, sinto em lhe informar, mas apenas com a resolução de vários exercícios você irá conseguir associar corretamente o que cada um descreve.
Características das grandezas vetoriais:
Módulo ou magnitude: Valor numérico (exemplos: 2, 10, 55);
Direções: Vertical, horizontal e diagonal;
Sentidos: Esquerda, direita, para cima e para baixo.
Exemplos de grandezas vetoriais:
1) Deslocamento [$m$ – Metros];
2) Velocidade [$\frac{m}{s}$ – Metros por segundo];
3) Aceleração [$\frac{m}{s^2}$ – Metros por segundo ao quadrado];
4) Força [$N$ – Newtons];
Posição [$m$ – Metros].
Grandezas fundamentais
Existem sete grandezas tidas como fundamentais na física, elas foram definidas pelo SI, assim como suas unidades, que são justamente as unidades-padrão, utilizadas por todo o mundo.
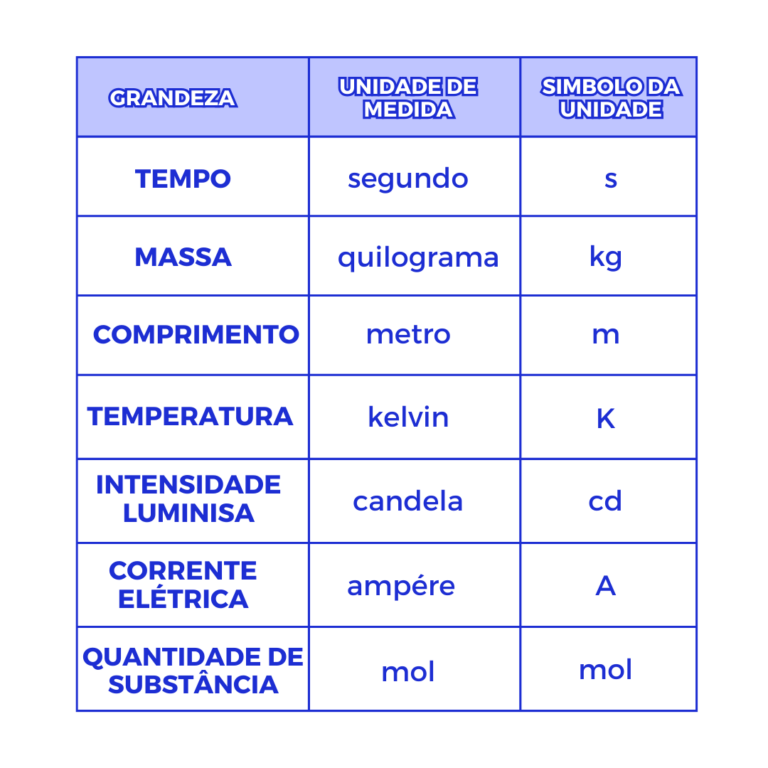
A partir delas surgem todas as outras grandezas conhecidas.
Grandezas derivadas
As grandezas que derivam das fundamentais, ou seja, que são formadas pela junção de duas ou mais dentre as sete principais, são denominadas “grandezas derivadas”, e suas unidades de medida são uma mescla das unidades-padrão; na tabela abaixo podemos ver algumas delas:
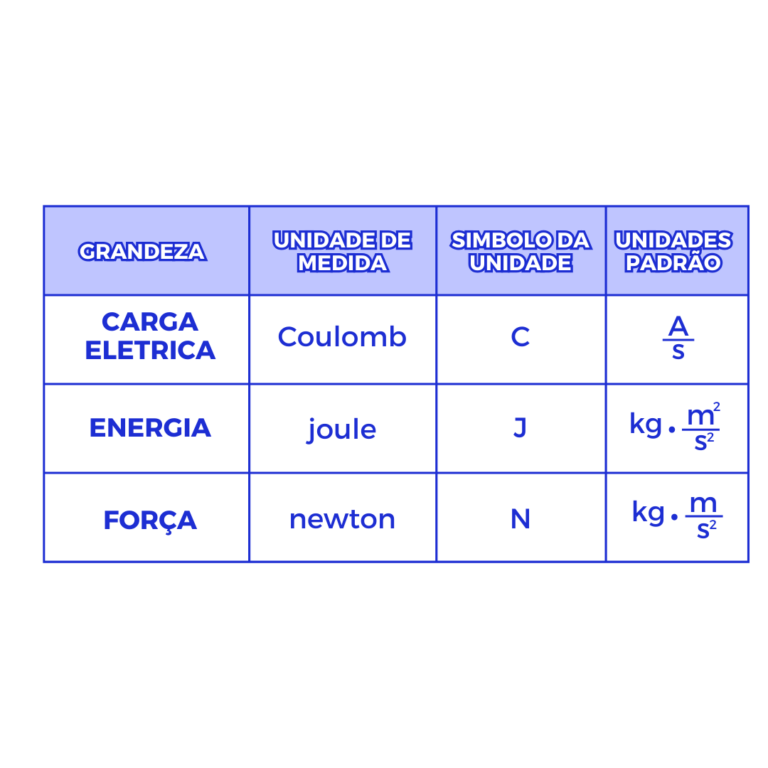
Grandezas direta e inversamente proporcionais
Podemos classificar as grandezas de uma outra forma, que pode nos ajudar a entender uma das formas em que elas se relacionam entre si. Dizemos que as grandezas são diretamente proporcionais em uma equação, quando ao aumentarmos uma, a outra tende a aumentar também, exemplo:
$$v=\frac{\Delta s}{\Delta t}$$
Tomemos a equação da velocidade média, caso aumentemos a distância percorrida ($\Delta s$), a velocidade aumentará
$$v=\frac{\Delta s}{\Delta t}$$
$$v=\frac{20}{10}=2$$
$$v=\frac{40}{10}=4$$
$$v=\frac{100}{10}=10$$
Então, podemos dizer que a grandeza “distância percorrida”, é diretamente proporcional a grandeza “velocidade”. Utilizando essa mesma equação, podemos visualizar o conceito de grandezas inversamente proporcionais, que por sua vez são grandezas que se comportam de forma oposta no que diz respeito a seus valores, quando uma aumenta a outra diminui e vice-versa. Na equação da velocidade média, se aumentarmos o tempo, a velocidade diminuirá de valor.
$$v=\frac{\Delta s}{\Delta t}$$
$$v=\frac{100}{10}=10$$
$$v=\frac{100}{20}=5$$
$$v=\frac{100}{50}=2$$
