Caso tenha dúvidas em relação as resoluções, recomendo que leia os artigos de operações básicas, regra de sinais, equação e equação logarítmica. Se quiseres questões contextualizadas sobre equação logarítmica, futuramente haverá artigo aqui no blog.
Questão 1:
Resolva a equação logarítmica abaixo
$$\log_{2}x=4$$
Resolução da questão 1:
Condição de existência:
$$x>0$$
Resolvendo a questão:
$$\log_{2}x=4$$
$$x=2^4$$
$$x=16$$
Prova real da questão 1:
$$\log_{2}x=4$$
$$\log_{2}16=4$$
$$4=4$$
Questão 2:
Resolva a equação logarítmica abaixo
$$\log_{3}(x-1)=2$$
Resolução da questão 2:
Condição de existência:
$$x-1>0$$
$$x>1$$
Resolvendo a questão:
$$\log_{3}(x-1)=2$$
$$x-1=3^2$$
$$x-1=9$$
$$x-1=9$$
$$x=9+1$$
$$x=10$$
Prova real da questão 2:
$$\log_{3}(x-1)=2$$
$$\log_{3}(10-1)=2$$
$$\log_{3}9=2$$
$$2=2$$
Questão 3:
Resolva a equação logarítmica abaixo
$$\log_{x}32=5$$
Resolução da questão 3:
Condições de existência:
1)
$$x>0$$
2)
$$x\neq0$$
Resolvendo a questão:
$$\log_{x}32=5$$
$$x^5=32$$
$$\sqrt[5]{x^5}=\sqrt[5]{32}$$
$$x=2$$
Prova real da questão 3:
$$\log_{x}32=5$$
$$\log_{2}32=5$$
$$5=5$$
Questão 4:
Determine, se existir, a solução da equação logarítmica abaixo
$$\log_{x^4}64=\frac{1}{2}$$
Resolução da questão 4:
Condições de existência:
1)
$$x\neq1$$
2)
$$x\neq0$$
Resolvendo a questão:
$$\log_{x^4}64=\frac{1}{2}$$
$$(x^4)^{\frac{1}{2}}=64$$
$$x^{\frac{4}{2}}=64$$
$$x^2=64$$
$$\sqrt{x^2}=\sqrt{64}$$
$$x=\pm8$$
Prova real da questão 4:
Substituindo $x=8$
$$\log_{x^4}64=\frac{1}{2}$$
$$\log_{8^4}64=\frac{1}{2}$$
$$\log_{8^4}8^2=\frac{1}{2}$$
$$\frac{\log_{8}8^2}{\log_{8}8^4}=\frac{1}{2}$$
$$\frac{2}{4}=\frac{1}{2}$$
$$\frac{1}{2}=\frac{1}{2}$$
Substituindo $x=-8$
$$\log_{x^4}64=\frac{1}{2}$$
$$\log_{(-8)^4}64=\frac{1}{2}$$
$$\log_{4096}64=\frac{1}{2}$$
$$\log_{8^4}8^2=\frac{1}{2}$$
$$\frac{\log_{8}8^2}{\log_{8}8^4}=\frac{1}{2}$$
$$\frac{2}{4}=\frac{1}{2}$$
$$\frac{1}{2}=\frac{1}{2}$$
Questão 5:
Determine, se existir, a solução da equação logarítmica abaixo
$$\log(x+1)=\log(-x+3)$$
Resolução da questão 5:
Condições de existência:
1)
$$x+1>0$$
$$x>-1$$
2)
$$-x+3>0$$
$$-x>-3$$
$$x<3$$
Resolvendo a questão:
$$\log(x+1)=\log(-x+3)$$
$$x+1=-x+3$$
$$x+x=3-1$$
$$2x=2$$
$$x=\frac{2}{2}$$
$$x=1$$
Prova real da questão 5:
$$\log(x+1)=\log(-x+3)$$
$$\log(1+1)=\log(-1+3)$$
$$\log2=\log2$$
Questão 6:
Determine, se existir, a solução da equação logarítmica abaixo
$$\log_{3}x^2=\log_{3}50-log_{3}2$$
Resolução da questão 6:
Condição de existência:
$$x\neq0$$
Resolvendo a questão:
$$\log_{3}x^2=\log_{3}50-log_{3}2$$
$$\log_{3}x^2=\log_{3}\frac{50}{2}$$
$$\log_{3}x^2=\log_{3}25$$
$$x^2=25$$
$$\sqrt{x^2}=\sqrt{25}$$
$$x=\pm5$$
Prova real da questão 6:
Substituindo $x=5$
$$\log_{3}x^2=\log_{3}50-log_{3}2$$
$$\log_{3}5^2=\log_{3}\frac{50}{2}$$
$$\log_{3}25=\log_{3}25$$
Substituindo $x=-5$
$$\log_{3}x^2=\log_{3}50-log_{3}2$$
$$\log_{3}(-5)^2=\log_{3}\frac{50}{2}$$
$$\log_{3}25=\log_{3}25$$
Questão 7:
Ache o valor de $x$ para que a igualdade seja verdadeira
$$\log_{2x}(3x-4)=1$$
Resolução da questão 7:
Condições de existência:
1)
$$3x-4>0$$
$$3x>4$$
$$x>\frac{4}{3}$$
$$x>1,33$$
2)
$$2x>0$$
$$x>\frac{0}{2}$$
$$x>0$$
3)
$$2x\neq1$$
$$x\neq\frac{1}{2}$$
Resolvendo a questão:
$$\log_{2x}(3x-4)=1$$
$$\frac{\log(3x-4)}{\log2x}=1$$
$$\log(3x-4)=1.\log2x$$
$$\log(3x-4)=\log2x$$
$$3x-4=2x$$
$$3x-2x=4$$
$$x=4$$
Prova real da questão 7:
$$\log_{2x}(3x-4)=1$$
$$\log_{2.4}(3.4-4)=1$$
$$\log_{8}(12-4)=1$$
$$\log_{8}8=1$$
$$1=1$$
Questão 8:
Ache o valor de $x$ para que a igualdade seja verdadeira
$$\log_{-x+1}(-3x)=8^0$$
Resolução da questão 8:
Condições de existência:
1)
$$-x+1>0$$
$$-x>-1$$
$$x<1$$
2)
$$-3x>0$$
$$3x<0$$
$$x<\frac{0}{3}$$
$$x<0$$
Resolvendo a questão:
$$\log_{-x+1}(-3x)=8^0$$
$$\log_{-x+1}(-3x)=1$$
$$\frac{\log(-3x)}{\log(-x+1)}=1$$
$$\log(-3x)=1.\log(-x+1)$$
$$-3x=-x+1$$
$$-3x+x=1$$
$$-2x=1$$
$$x=-\frac{1}{2}$$
Prova real da questão 8:
$$\log_{-x+1}(-3x)=8^0$$
$$\log_{-(-\frac{1}{2})+1}(-3\cdot(-\frac{1}{2}))=1$$
$$\log_{\frac{1}{2}+1}(\frac{3}{2})=1$$
$$\log_{\frac{1+2}{2}}(\frac{3}{2})=1$$
$$\log_{\frac{3}{2}}(\frac{3}{2})=1$$
$$1=1$$
Questão 9:
Ache o valor de $x$ para que a igualdade seja verdadeira
$$(\log_{2}x)^2-3\log_{2}x=-2$$
Resolução da questão 9:
Condição de existência:
$$x>0$$
Resolvendo a questão:
$$(\log_{2}x)^2-3\log_{2}x=-2$$
Vou substituir o $\log_{2}x$ por $y$, para poder resolver a questão
$$y^2-3y=-2$$
$$y^2-3y+2=0$$
$$a=1,b=-3,c=2$$
$$y=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$$
$$y=\frac{-(-3)\pm\sqrt{(-3)^2-4.1.2}}{2.1}$$
$$y=\frac{3\pm\sqrt{9-8}}{2}$$
$$y=\frac{3\pm\sqrt{1}}{2}$$
$$y=\frac{3\pm1}{2}$$
$$y_1=\frac{3+1}{2}=\frac{4}{2}=2$$
$$y_2=\frac{3-1}{2}=\frac{2}{2}=1$$
Ainda não achei a resposta, pois a resposta deve ser em relação à $x$
1)
$$y_1=2$$
$$\log_{2}x=2$$
$$x=2^2$$
$$x=4$$
2)
$$y_2=1$$
$$\log_{2}x=1$$
$$x=2^1$$
$$x=2$$
Prova real da questão 9:
Substituindo $x=4$
$$(\log_{2}x)^2-3\log_{2}x=-2$$
$$(\log_{2}4)^2-3\log_{2}4=-2$$
$$2^2-3.2=-2$$
$$4-6=-2$$
$$-2=-2$$
Substituindo $x=2$
$$(\log_{2}x)^2-3\log_{2}x=-2$$
$$(\log_{2}2)^2-3\log_{2}2=-2$$
$$1^2-3.1=-2$$
$$1-3=-2$$
$$-2=-2$$
Questão 10:
Ache o valor de $x$ para que a igualdade seja verdadeira
$$\log_{3}(x-2).(x+1)=\log_{3}x^2$$
Resolução da questão 10:
Condições de existência:
1)
$$(x-2).(x+1)>0$$
$$x^2-x-2>0$$
$$x^2-x-2=0$$
$$a=1,b=-1,c=-2$$
$$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$$
$$x=\frac{-(-1)\pm\sqrt{(-1)^2-4.1.(-2)}}{2.1}$$
$$x=\frac{1\pm\sqrt{1+8}}{2}$$
$$x=\frac{1\pm\sqrt{9}}{2}$$
$$x=\frac{1\pm3}{2}$$
$$x_1=\frac{1+3}{2}=\frac{4}{2}=2$$
$$x_2=\frac{1-3}{2}=\frac{-2}{2}=-1$$
Devemos analisar o gráfico para entender para quais valores de $x$ teremos valores maiores que zero, ou seja, positivos.
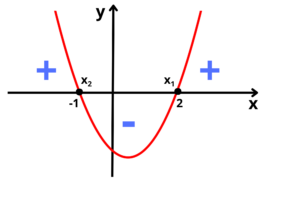
Para valores menores que $-1$ e maiores que $2$, temos o gráfico acima do eixo $x$, portanto:
$$x<-1$$
e
$$x>2$$
2)
$$x\neq0$$
Resolvendo a questão:
$$\log_{3}(x-2).(x+1)=\log_{3}x^2$$
$$\log_{3}x^2-x-2=\log_{3}x^2$$
$$x^2-x-2=x^2$$
$$x^2-x-2-x^2=0$$
$$-x-2=0$$
$$-x=2$$
$$x=-2$$
Prova real da questão 10:
$$\log_{3}(x-2).(x+1)=log_{3}x^2$$
$$\log_{3}(-2-2).(-2+1)=log_{3}(-2)^2$$
$$\log_{3}(-4).(-1)=log_{3}4$$
$$\log_{3}4=log_{3}4$$
Formado em Eletrotécnica pelo IFRN, além de ter cursos de Matemática Básica e Cálculo pela empresa Help Engenharia.
