Dois conceitos matemáticos que são muito vistos no ensino fundamental, mas que podem ser úteis em diversos momentos da vida acadêmica de qualquer estudante, o MMC e o MDC serão os protagonistas desse artigo, onde explicarei o que significam e como usá-los.
O que é MMC?
MMC é a abreviação para Mínimo Múltiplo Comum, e como o nome sugere, se trata de um número que é o menor múltiplo de dois ou mais números.
Como calcular o MMC?
Podemos listar alguns múltiplos dos números que queremos encontrar o MMC, e então comparar as listas, o menor número que for múltiplo que estiver presente em todas as listas, será o MMC.
Exemplo:
Encontre o MMC entre
Primeiro, vamos escrever uns seis múltiplos dos dois números
Múltiplos de
Múltiplos de
Podemos perceber que o número
Imagina só se ao invés de termos dois números pequenos, tivéssemos números maiores e em maior quantidade, daria um trabalhão para listarmos os múltiplos, mas não se desespere, há uma maneira prática e rápida para descobrirmos o MMC de quaisquer números. Primeiramente, organize os números um do lado do outro, separando-os com uma vírgula, depois, trace uma linha do lado direito deles
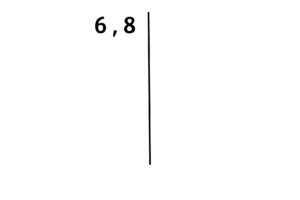
No lado direito da linha, você irá colocar um número primo que divida pelo menos um dos dois números, começando pelo
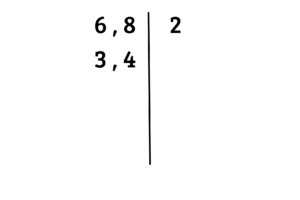
O
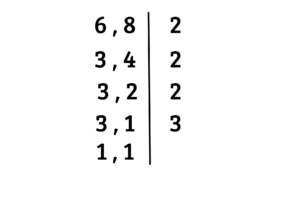
Uma vez finalizado o processo, multiplique os números que estão à direita da linha e o resultado dessa multiplicação será o MMC entre
Já sabíamos que o MMC era
O que é MDC?
MDC é a abreviação para Máximo Divisor Comum, e é o maior número que divide dois ou mais números.
Como calcular o MDC?
Listarmos todos os divisores dos números que queremos encontrar o MDC, e comparamos as listas, o maior número que estiver contido em todas as listas será o MDC.
Exemplo:
Encontre o MDC entre
Iniciamos montando a lista de divisores dos dois números
Divisores de
Divisores de
O maior número que é divisor tanto de
Da mesma forma que no MMC, caso tivéssemos que calcular o MDC de vários números, que possuem vários divisores, seria demasiadamente trabalhoso realizar esse processo, então, podemos utilizar um método (bem parecido com o que aprendemos no MMC) que nos permite achar o maior divisor facilmente. Primeiro, escreva os números um ao lado do outro, separando-os com uma vírgula e trace uma linha à direita deles
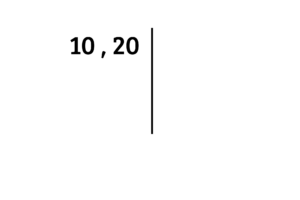
Agora, escreva do lado direito da linha um número primo que divida o
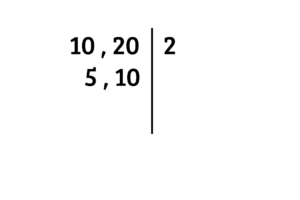
O
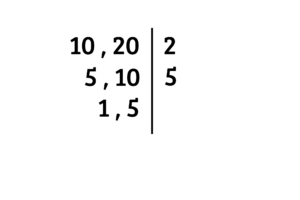
Não há um número primo capaz de dividir o
Com a prática, você irá realizar essa técnica rapidamente, e não irá confundir com o processo para achar o MMC. E a ponto de curiosidade, o que fizemos nesses dois métodos práticos, foi fatoração por números primos.
Método alternativo para achar MMC e MDC:
Há um jeito diferente de calculá-los, que pode parecer complicado para alguns, mas intuitivo para outros, sendo assim, importante conhecer para aumentar sua bagagem de ferramentas matemáticas.
MMC: Primeiro, fatoramos os números em fatores primos se multiplicando, juntamos as potências de mesma base e por fim, multiplicamos as potências de maior expoente.
Exemplo:
Ache o MMC entre
Vamos fatorar ambos
1)
2)
Juntamos as potências de mesma base
1)
2)
Agora, multiplicamos as potências de bases distintas, com os maiores expoentes
Podemos escrever a resposta em sua forma “formal”:
MDC: O método é quase igual ao de MMC, com uma pequena diferença. Para calculá-lo, fatoramos os números em fatores primos, depois juntamos as bases que se repetem e por fim, multiplicamos os fatores de menor expoente.
Exemplo:
Ache o MDC entre
Primeiro, transformamos eles na multiplicação entre números primos
1)
2)
Em seguida, juntamos a potências de mesma base
1)
2)
Agora pegamos as potências de base diferentes de menor expoente e a multiplicamos, o resultado será o MDC entre
A forma “formal” de escrever a resposta é:
Exercícios resolvidos de MMC e MDC
1. Encontre o MDC entre
Aplicamos o método prático para MDC, organizamos os números lado a lado, traçamos uma linha à direita, escrevemos os números primos que dividem ambos os números, executamos as divisões e repetimos isso até não encontrarmos um número primo que divida todo mundo
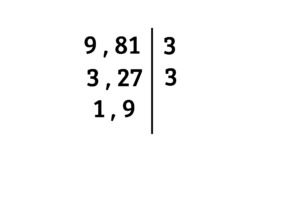
Para finalizar, multiplicamos os números à direita da linha
Portanto,
2. Encontre o MMC entre
Aplicamos o método prático para MMC, organizamos os números lado a lado, traçamos uma linha à direita, escrevemos os números primos que dividem pelo menos um dos dois números, executamos as divisões e repetimos isso até sobrar somente números

Então, multiplicamos os números do lado direito da linha
Portanto,
3. Encontre o MMC e o MDC entre
Realizamos o processo para encontrar o MMC
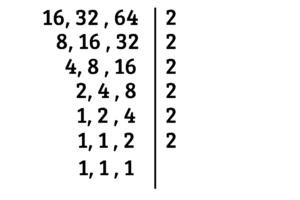
E multiplicamos os números primos que estão no lado direito da linha
Obtemos o MMC, que é $64, agora calculamos o MDC
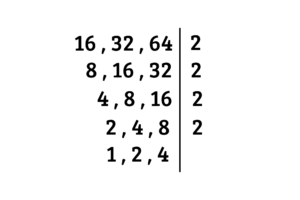
Multiplicamos os números à direita e finalizamos a questão ao encontrarmos o MDC
Importância de aprender MMC e MDC
Além de serem conhecimentos matemáticos básicos que podem ser cobrados em questões de nível fundamental, eles são extremamente úteis ao somar frações com denominadores diferentes, além de serem utilizados na simplificação de termos em uma equação.

Formado em Eletrotécnica pelo IFRN, além de ter cursos de Matemática Básica e Cálculo pela empresa Help Engenharia.




