O que é logaritmo?
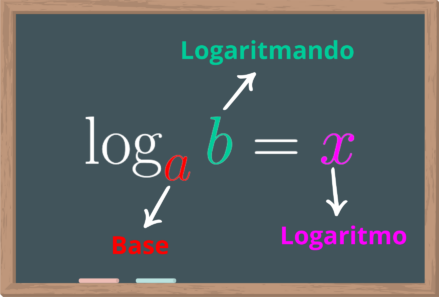
Temido por uns, amado por outros, o logaritmo é uma operação matemática que nos permite descobrir o expoente de uma potência, conhecendo sua base e o resultado da potência. Sua forma geral é:
$log_{B}A=C$
Essa expressão é lida: “Log de $A$ na base $B$”, sendo $B$ a base do log (representa a base de uma potência qualquer) e $C$ é o expoente que eleva a base para resultar em $A$ (o $A$ é chamado de logaritmando). Até então, pode parecer confuso, mas fica comigo até o final, que vai valer à pena.
Como resolver um logaritmo?
Para resolvermos um log, fazemos a seguinte pergunta: “Qual expoente a base precisa ter para que resulte no número que está no logaritmando?” para respondermos essa pergunta, é necessário dominarmos tanto a potenciação, quanto a radiciação (não se preocupe, pois tem artigos no blog sobre esses assuntos). Podemos resolver de forma direta, caso já saibamos a resposta, ou manipulamos o logaritmando para transformarmos ele em uma potência com a mesma base que a base do log.
Exemplo 1:
Ache o resultado de $log_{2}8$
Primeiro, identificamos a base e o logaritmando, nesse caso a base é $2$ e o logaritmando é $8$, então verificamos: temos que elevar o $2$ a quanto para chegarmos em $8$? Vamos testar alguns valores
$2^1=2$
$2^2=2.2=4$
$2^3=2.2.2=8$
O valor que queremos é $3$, pois $2^3$ é igual à $8$, então a resposta do log é $3$
$log_{2}8=3$
Podemos escrever a resposta da seguinte forma:
$B^C=A$
Substituindo os valores
$2^3=8$
Exemplo 2:
Ache o resultado de $log_{3}81$
Que valor elevamos o $3$ para chegarmos em $81$? Agora resolverei da outra forma, sabemos que $81$ é o mesmo que $9.9$, então podemos reescrever o log
$log_{3}9.9$
Só que $9$, é a mesma coisa que $3^2$
$log_{3}3^2.3^2$
Temos duas potências de bases iguais se multiplicando no logaritmando, então podemos utilizar uma propriedade de potenciação para simplificar
$log_{3}3^2.2^2=log_{3}3^{2+2}=log_{3}3^4$
Transformamos o $81$ em uma potência de base $3$, que não coincidentemente é igual à base do log, com isso, já conseguimos saber a resposta, pois constatamos que $81=3^4$, portanto, o expoente que o $3$ deve ter para resultar em $81$ é $4$
$log_{3}81=4$
Considerações importantes sobre o logaritmo
Nem sempre será tão fácil identificar a resposta do logaritmo, precisando as vezes fazer manipulações no logaritmando e na base, para simplificar o log e facilitar a visualização da resposta, então é essencial que saibamos algumas considerações que podem facilitar nossa vida
a) O $A$ deve maior que $0$, já a base ($B$), deve ser maior que $0$ e diferente de $1$;
b) Se a base for igual ao logaritmando, então a resposta do log será $1$;
Exemplos:
1) $log_{2}2=1$
2) $log_{7}7=1$
3) $log_{245}245=1$
c) Se o logaritmando ($A$) for $1$, independentemente do valor da base, o resultado do log será zero, pois qualquer número elevado à $0$ é igual à $1$;
Exemplos:
1) $log_{3}1=0$
2) $log_{10}1=0$
3) $log_{200}1=0$
d) Se o log não tiver uma base explícita (visível), significa que a base é igual à $10$;
Exemplos:
1) $log_{}25=log_{10}25$
2) $log_{}10=log_{10}10$
3) $log_{}π=log_{10}π$
e) Se uma potência estiver elevada a um log com base igual a base dela, o logaritmando será a resposta dessa expressão.
Exemplos:
1) $2^{log_{2}16}=16$
2) $3^{log_{3}81}=81$
3) $10^{log_{}1000}=1000$
O que é ln?
Denominado “logaritmo natural”, muitas pessoas o encaram como algo de outro mundo, em parte porque já possuem dificuldade em entender o que é logaritmo e por não ser explicado para elas de uma forma simples. Assim como pi ($π$) é um número irracional e constante, ou seja, um valor que não pode ser escrito na forma de fração, possui infinitas casas decimais e não varia, existe uma constante chamada constante de Euler, que é um número fundamental da matemática e aparece em várias aplicações, a representação dela é “$e$”, e ela vale aproximadamente $2,718$. O ln é basicamente, um log cuja base é a constante de Euler, ou seja, é um logaritmo na base $e$:
$log_{e}=ln$
O surgimento dessa simbologia se deu pelo fato de aparecer tantas vezes $\log_{e}$ nos cálculos, que os matemáticos acharam mais conveniente chamar tudo isso de algo mais simples, daí vem o ln.
Propriedades dos logaritmos
Como dito anteriormente, as vezes não será tão intuitivo e simples encontrar a resposta de um log, e além das considerações, existem quatro propriedades que irão lhe fazer poupar muito tempo e evitar dores de cabeça desnecessárias ao resolver logaritmos.
Log de uma multiplicação:
Quando tivermos dois (ou mais números) se multiplicando no logaritmando, ao invés de calcular essa multiplicação, que pode resultar em um valor muito alto, podemos separar em dois logs de mesma base se somando, cujos logaritmandos serão justamente, os números que estavam se multiplicando.
Exemplo 1:
Ache o resultado de $log_{2}16.8$
Temos dois números se multiplicando no logaritmando, então, podemos separar esse log em dois logs de base $2$, com logaritmandos $16$ e $8$, se somando
$log_{2}16.8=log_{2}16+log_{2}8$
Ou seja, transformamos o log de uma multiplicação, em uma soma de logs mais simples, e resolvendo eles, teremos a resposta do log original
$log_{2}16+log_{2}8=4+3=7$
Então a resposta do $log_{2}16.8$ é $7$. Uma forma de conferir se você acertou, é calcular quanto é $2^7$ e comparar com o resultado da multiplicação do logaritmando, se forem iguais, então você acertou. É trabalhoso, mas se você não possuir uma calculadora científica, ou não puder usá-la, será útil para saber se cometeu algum erro no cálculo.
Exemplo 2:
Ache o resultado de $log_{4}64$
O logaritmando possui um número um pouco grande, no entanto, podemos transformar ele em uma multiplicação de números menores, nesse caso $64$ é igual à $4.4.4$, então podemos reescrever o log como:
$log_{4}64=log_{4}4.4.4$
Agora podemos separar esse log utilizando a propriedade e resolvê-lo
$log_{4}4.4.4=log_{4}4+log_{4}4+log_{4}4=1+1+1=3$
Portanto,
$log_{4}64=3$ ou $4^3=64$
Log de uma divisão:
E se tivermos uma divisão no logaritmando? Simples, podemos transformar o log em dois logs se subtraindo, e os logaritmandos deles serão respectivamente os valores do numerador e denominador da fração (lembrando que eles devem possuir a mesma base do original). Podes simplificar a fração antes de resolver, mas haverá frações que não resultarão em valores exatos, para esses casos essa propriedade será indispensável.
Exemplo 1:
Ache o resultado de $log_{5}\frac{125}{25}$
Caso não saibas o resultado da divisão de $125$ por $5$, podes transformar essa expressão em log na base $5$ de $125$ menos log na base $5$ de $25$. E ao resolvermos ambos, teremos o resultado do log original, e isso funcionará para todas as propriedades, ou seja, ao resolvermos a expressão depois de aplicada(s) a(s) propriedade(s), acharemos o resultado do primeiro log de todos.
$log_{5}\frac{125}{25}=log_{5}125-log_{5}25=3-2=1$
Portanto,
$log_{5}\frac{125}{25}=1$
Por curiosidade, $125$ dividido por $25$ é igual à $5$, por isso que o resultado deu $1$.
Exemplo 2:
Ache o resultado de $log_{4}\frac{64}{256}$
Separamos em dois logs se subtraindo
$log_{4}\frac{64}{256}=log_{4}64-log_{4}256=3-4=-1$
Isso mesmo, você não está enxergando mal, a resposta é um número negativo, pois o resultado da divisão é $\frac{1}{4}$, que é a mesma coisa que $4^{-1}$, essa manipulação é possível graças a uma “propriedade” de potenciação.
Log de uma potência:
Essa propriedade só não é melhor que a próxima, mas é impressionante o que ela permite fazer. Basicamente, podemos pegar o expoente que estiver elevando o logaritmando, e “tombá-lo”, onde ele passará a multiplicar o log, só que diferente da regra do tombo nas derivadas (assunto do ensino superior), ao fazermos isso, não alteraremos em nada o valor do log, somente reescreveremos ele de uma forma equivalente. Esse artifício é extremamente útil quando o expoente for uma fração.
Exemplo 1:
Ache o resultado de $log_{2}\sqrt[3]{4^2}$
Temos uma raiz no logaritmando, mas não criemos pânico, primeiramente, transformaremos essa raiz em expoente, utilizando uma propriedade de radiciação
$log_{2}4^{\frac{2}{3}}$
Com a terceira propriedade do log, podemos tombar esse expoente, e ele agora ficará multiplicando o log de $4$ na base $2$
$log_{2}4^{\frac{2}{3}}=\frac{2}{3}.log_{2}4=\frac{2}{3}.2=\frac{4}{3}$
Por mais estranho que pareça, a resposta está correta
$log_{2}\sqrt[3]{4^2}=\frac{4}{3}$
Aqui vai a prova:
$log_{2}\sqrt[3]{4^2}=log_{2}\sqrt[3]{(2^2)^2}=log_{2}\sqrt[3]{2^4}=log_{2}2^{\frac{4}{3}}=\frac{4}{3}$
Exemplo 2:
Ache o resultado de $log_{6}\frac{\sqrt{6}}{36}$
Na maioria dos exercícios, será necessário utilizar mais de uma propriedade, nesse caso, temos uma divisão no logaritmando, então podemos separar em dois logs se subtraindo
$log_{6}\frac{\sqrt{6}}{36}=log_{6}\sqrt{6}-log_{6}36$
Como a raiz quadrada de $6$ não é um número exato, é interessante transformarmos a raiz em expoente e utilizarmos a propriedade do log de uma potência para tombá-lo
$log_{6}\sqrt{6}-log_{6}36=log_{6}6^{\frac{1}{2}}-log_{6}36$
$\frac{1}{2}.log_{6}6-log_{6}36$
Então, resolvemos os logs e somamos os resultados para achar a resposta da questão
$\frac{1}{2}.log_{6}6-log_{6}36=\frac{1}{2}.1-2=\frac{1}{2}-2=\frac{-3}{2}$
Mudança de base:
Até agora, só vimos casos em que a base do log é igual ou menor que o logaritmando, mas e se ela for maior? Como acharemos um expoente que transforma um número maior em um número menor, é para resolver casos como esse ou quando a base é uma fração, que existe a quarta e indiscutivelmente sensacional, propriedade de logaritmo.
Com ela podemos mudar a base do nosso log, e para isso, montamos uma divisão (fração) de dois logs, cujo logaritmando do numerador será o mesmo que o log original e o logaritmando do denominador será a base antiga, mas qual será a base desses logs? A que você quiser, isso mesmo, podemos escolher qualquer base, independentemente do valor (contanto que ela seja maior que $0$), só que para podermos calcular manualmente, é importante escolhermos uma base que nos permita resolver tanto o log do numerador, quanto o do denominador. Vamos para os exemplos.
Exemplo 1:
Ache o resultado de $log_{8}2$
Vejamos, qual expoente que elevamos o $8$ para chegar em $2$? Difícil né, pois $8^1=8$, que é maior que $2$, então utilizaremos a mudança de base ao nosso favor. Primeiramente, escreveremos uma fração, onde o numerador será o log de $2$ (logaritmando do log original) e o denominador será o log de $8$ (base antiga)
$\frac{log_{?}2}{log_{?}8}$
Mas falta definirmos uma coisa, qual base escolhemos? Uma base que possamos resolver ambos os logs, a base $4$ e base $8$ permitiriam resolver o log de $8$, mas não o log de $2$, só que a base $2$, permite a solução de ambos
$\frac{log_{?}2}{log_{?}8}=\frac{log_{2}2}{log_{2}8}$
Agora é só resolvermos e comemorarmos!
$\frac{log_{2}2}{log_{2}8}=\frac{1}{3}$
Portanto,
$log_{8}2=\frac{1}{3}$
Duas observações importantes, primeiro, a nova base escolhida deve ser a mesma para os dois logs, e você pode escolher sim, quaisquer números para ser a nova base, só que você ou terá mais trabalho para resolver, ou não conseguirá resolver manualmente, tendo que utilizar uma calculadora para achar a resposta.
Exemplo 2:
Ache o resultado de $log_{3.27}9$
Temos uma base maior que o logaritmando, portanto, vamos utilizar a mudança de base
$log_{3.27}9=\frac{log_{?}9}{log_{?}3.27}$
A nova base será $3$, pois tanto o log de $9$, quanto o log de $3.27=81$, podem ser resolvidos na base $3$. Poderíamos resolver a multiplicação que está no logaritmando de baixo, mas vamos supor que você não saiba o resultado da multiplicação ou o log de $3$ na base $81$, podemos utilizar a primeira propriedade vista nesse artigo para simplificar a expressão
$\frac{log_{?}9}{log_{?}3.27}=\frac{log_{3}9}{log_{3}3.27}$
$\frac{log_{3}9}{log_{3}3+log_{3}27}$
Basta resolvermos os três logs e partir para o abraço
$\frac{log_{3}9}{log_{3}3+log_{3}27}=\frac{2}{1+3}=\frac{2}{4}=\frac{1}{2}$
O que é cologaritmo?
Pouco conhecido, o colog é um tipo especial de logaritmo e saber sobre ele pode ajudar a resolver alguns tipos específicos de questões. Sua representação geral é:
$colog_{B}A=-log_{B}A$
Ou
$colog_{B}A=log_{B}\frac{1}{A}$
Exemplos:
1) $colog_{4}16=-log_{4}16$
2) $colog_{36}6=-log_{36}6$
3) $colog_{2}8=log_{2}\frac{1}{8}$
Exercícios resolvidos de logaritmo
1. Se $log_{}2\approx0,3$, $log_{}3\approx0,5$ e $log_{}5\approx0,7$, calcule $log_{}30$
A questão nos dá o valor aproximado de três logs, e isso não é por acaso, de alguma forma, precisamos manipular o $log_{}30$ para chegarmos nos logs que foram mencionados no enunciado, e para isso, utilizaremos a boa e velha matemática básica e uma propriedade de log. Primeiramente, vamos analisar o $30$, podemos reescrevê-lo como $2.15$ ou $3.10$, em ambos os casos, fizemos aparecer um dos números que precisamos encontrar, utilizarei o $3.10$
$log_{}30=log_{}3.10$
O $10$, por sua vez, é a mesma coisa que $2.5$, e olha só, temos os outros dois números que faltavam, vamos reescrever o log utilizando essa informação
$log_{}3.10=log_{}3.2.5$
Temos o log de uma multiplicação de três termos, podemos separar em três logs de mesma base, se somando
$log_{}3.2.5=log_{}3+log_{}2+log_{}5$
Encontramos os logs do enunciado, agora é só substituir eles pelos seus valores, somar tudo e assim, achar a resposta de $log_{}30$
$log_{}3+log_{}2+log_{}5=0,5+0,3+0,7\approx1,5$
Coloquei o sinal de aproximadamente, pois a questão nos deu valores aproximados, então a resposta final também é uma aproximação, há professores rigorosos que tiram pontos por causa disso, então é importante mencionar.
2. Se $log_{2}x+log_{4}x=3$, qual é o valor de $x$?
Temos uma equação, especificamente uma equação logarítmica, mas para resolvermos a questão, só precisamos saber que para achar o valor da variável (letra) em uma equação, basta isolarmos ela, ou seja, deixarmos ela sozinha em um dos lados da equação (caso tenha dúvida sobre equações, sugiro ler nosso artigo sobre ela).
Temos dois logs se somando, será que não poderíamos juntá-los? A resposta é sim, no entanto, é necessário deixar eles com a mesma base, pois para juntar temos semelhantes em uma equação, eles devem ser iguais. Vamos fazer a mudança para a base $2$, do $log_{4}x$
$log_{2}x+log_{4}x=3$
$log_{2}x+\frac{log_{2}x}{log_{2}4}=3$
Resolvemos o que está no denominador e somamos as frações
$log_{2}x+\frac{log_{2}x}{log_{2}4}=3$
$log_{2}x+\frac{log_{2}x}{2}=3$
$\frac{2.log_{2}x+log_{2}x }{2}=3$
$\frac{3.log_{2}x }{2}=3$
Agora, vamos passar tanto o $3$, quanto o $2$ para o lado direito da equação, para deixar o $log_{2}x$ sozinho
$\frac{3.log_{2}x }{2}=3$
$log_{2}x=\frac{2}{3}.3$
$log_{2}x=2$
Lembra de uma das considerações que foram feitas no início do artigo? Que $B^{log_{B}A}=A$, se transformarmos ambos os termos em expoentes de uma potência de base $2$, poderemos eliminar o log e deixar somente o $x$, e como em uma equação podemos fazer qualquer manipulação, desde que seja feito em ambos os lados da igualdade e que esteja matematicamente correto, isso é completamente possível
$log_{2}x=2$
$2^{log_{2}x}=2^2$
$x=2^2=4$
Então a respostas é $4$, e para conferirmos se acertamos, basta substituir na equação que foi dada no enunciado e se a igualdade for verdadeira, está correta a resposta
$log_{2}x+log_{4}x=3$
$log_{2}4+log_{4}4=3$
$2+1=3$
$3=3$
Importância de aprender logaritmo
O logaritmo é uma ferramenta excepcional, que permite transformar multiplicações em soma, divisões em subtrações, tombar o expoente de uma potência sem alterar o valor dela e nos permite escolher dentro de uma infinidade de valores, qual será a nova base para nosso log (nenhum outro assunto da matemática nos dá essa liberdade), além disso, para resolvermos algumas equações exponenciais mais complexas, cujo método de igualar bases seja inviável, o log pode solucionar o problema.
