Utilizados em representações de pontos em um espaço cartesiano, para indiciar as coordenadas de um vetor com três componentes e em funções de duas variáveis, os ternos ordenados tão importantes quanto os pares ordenados.
O que é um terno ordenado?
O terno ordenado é uma representação matemática de três elementos de um conjunto numérico, coordenadas de um vetor ou de um ponto em um espaço cartesiano. Sim, parece a mesma definição de par ordenado, e isso não é por acaso, pois o terno é uma extensão do par ordenado, suas aplicações são praticamente as mesmas e a ordem dos elementos importam, assim como nos pares. Portanto, o terno
Exemplos:
1)
2)
3)
A simbolização do terno ordenado se dá por um parêntese, com três elementos um do lado do outro, separados por uma vírgula, com cada um deles representando um determinado valor, pertencente geralmente ao conjunto dos números reais.
O valor
Como representar o terno ordenado no espaço cartesiano?
Diferentemente do par ordenado, o terno pode ser utilizado para demarcar pontos em um espaço cartesiano, não em um plano, ou seja, há três eixos (
De forma geral, para qualquer ponto, o terno terá a seguinte aparência:
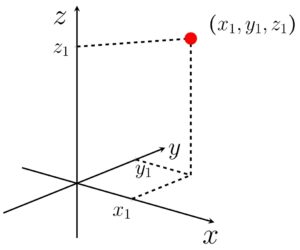
Onde os valores
Exercícios resolvidos de terno ordenado
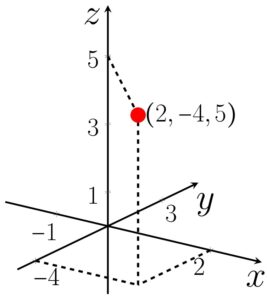
1. Represente graficamente o ponto de coordenadas
Já que temos um terno ordenado, representaremos o ponto em um espaço cartesiano. O primeiro elemento corresponde ao valor no eixo
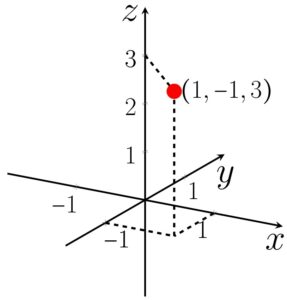
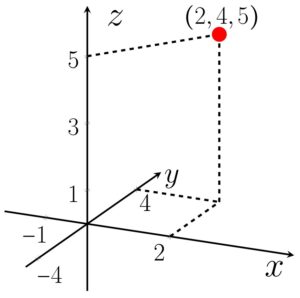
2. Dada a equação
Outra aplicação do terno é em equações de três variáveis, onde cada elemento deve ser substituído na variável correspondente para se obter determinado valor. Na questão acima, substituiremos
Então isolamos o
Nosso terno ordenado, ao substituirmos o valor que encontramos para
O que isso significa? Significa que ao substituirmos esses valores nas variáveis correspondentes, a igualdade se tornará verdadeira, pois é dito no enunciado da questão que o terno ordenado é uma solução para a equação. Por fim, vamos representar graficamente o terno, como foi pedido.
Formado em Eletrotécnica pelo IFRN, além de ter cursos de Matemática Básica e Cálculo pela empresa Help Engenharia.
