Muitos confundem os significados desses assuntos, pois eles são muito parecidos, se não tivermos cuidado ao estudá-los, ou se nos for ensinado de qualquer forma. Tentarei, dentro de minha capacidade, lhes explicar o que são e a diferença entre distância, posição e deslocamento.
O que é distância?
O mais simples dentre os três, distância é a quantidade total de espaço que percorremos, considerando todos os desvios e caminhos, independentemente se voltarmos para o mesmo lugar ou se pararmos em um lugar diferente de onde começamos a nos movimentar. Geralmente nos referimos a ela como “distância percorrida” ou “espaço percorrido”, que pode estar na unidade padrão, metros, ou em alguma outra unidade a depender da situação (quilômetros para distâncias maiores ou centímetros para movimentos muito sutis).
Exemplo 1:
Uma família pretende fazer uma viagem no final do ano, e apesar de eles poderem chegar mais cedo na cidade destino, preferem fazer um desvio para visitarem um familiar. Qual é a distância percorrida por eles durante todo o percurso?
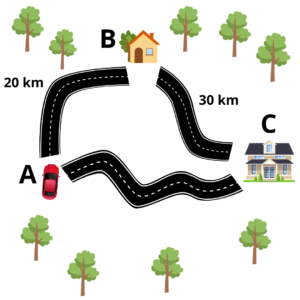
Para acharmos a distância que o carro percorreu, basta somarmos todos a distância, nesse caso em quilômetros, de todos os trajetos
$$20+30=50\;km$$
Simples não? Vale pontuar que a distância é uma medida positiva, ou seja, caso calculemos e encontremos um valor negativo, há algo errado em nosso cálculo.
Exemplo 2:
Se a mesma família do exercício anterior, tiverem esquecido de um compromisso e decidirem voltar assim que chegarem no destino (casa de férias), qual seria a distância percorrida?
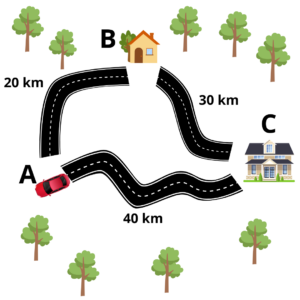
Mais uma vez, a única coisa que precisamos fazer é somar os valores em quilômetros dos trechos percorridos pelo veículo
$$20+30+40=90/;km$$
O que é posição?
Esse conceito pode ser um pouco “indigesto” de se compreender, mas tenhamos calma que não é algo de outro mundo. A posição, de forma bem simplificada, é o espaço exato em que o corpo (qualquer objeto que tenha massa) está ocupando no momento analisado, em outras palavras, é o local em que o objeto está. Só que para determinar a posição (ou espaço) de algo, precisamos ter um ponto de referência (referencial), podendo ser o ambiente em que ele se encontra (quarto, carro, terreno) ou até mesmo outro objeto.
Comecemos com um exemplo mais cotidiano, imaginemos uma estrada reta, que possui marcos demarcando os Km’s da pista, e suponhamos que há um carro percorrendo essa rodovia. Nos importa aqui apenas o lugar em que ele está, sem nos preocuparmos com velocidade, tamanho do carro ou curvas.
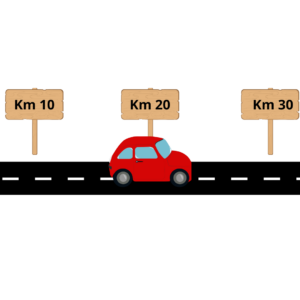
O carro acima está passando por um dos marcos da estrada, portanto, a posição dele nesse instante é $Km\;20$, ou seja, ele está no quilômetro $20$ da rodovia. Outra forma de analisar essa informação é dizer que “o carro está $20$ quilômetros de distância do início da rodovia”, levando em conta que a pista começa no $Km\;0$. O que nos permitiu delimitar a posição que o carro está foram os marcos, que são a nossa referência.
Antes de dar outros exemplos sobre esse conceito, preciso lhe explicar o que é trajetória. Em poucas palavras, a trajetória é o caminho que um corpo percorre, geralmente é representado por uma linha (reta ou não) que ilustra exatamente por onde o corpo passou no seu percurso. Se fôssemos desenhar a trajetória do carro daquela família que vimos anteriormente, teríamos o seguinte desenho:
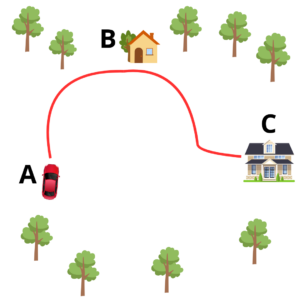
Traçamos trajetórias para que possamos ter referências a fim de nos ajudar a analisar a situação que envolve o movimento de um determinado corpo. Com isso em mente, tracemos uma trajetória com uma dimensão (que começa na esquerda e vai para a direita)
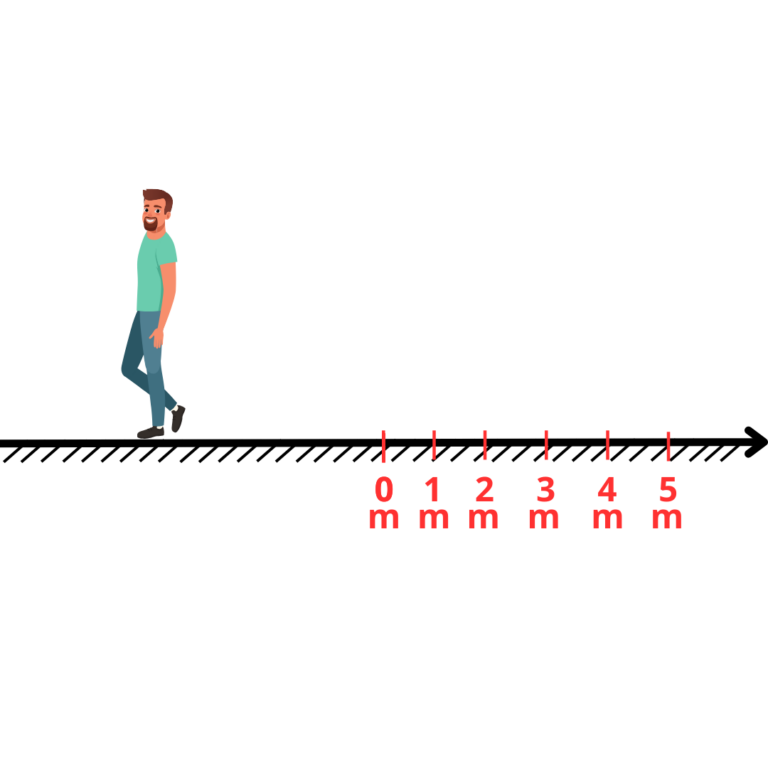
Imaginemos uma pessoa percorrendo essa trajetória
Então, vamos marcar o ponto que indica o início dessa trajetória, que seria o lugar onde o indivíduo começou a se movimentar, de onde ele partiu, esse será nosso ponto zero
Agora dividimos essa trajetória, partindo do zero, em vários pontos (marcos)
Para finalizar nosso cenário de estudo, vamos escolher um o “metro” como unidade de medida dos marcos
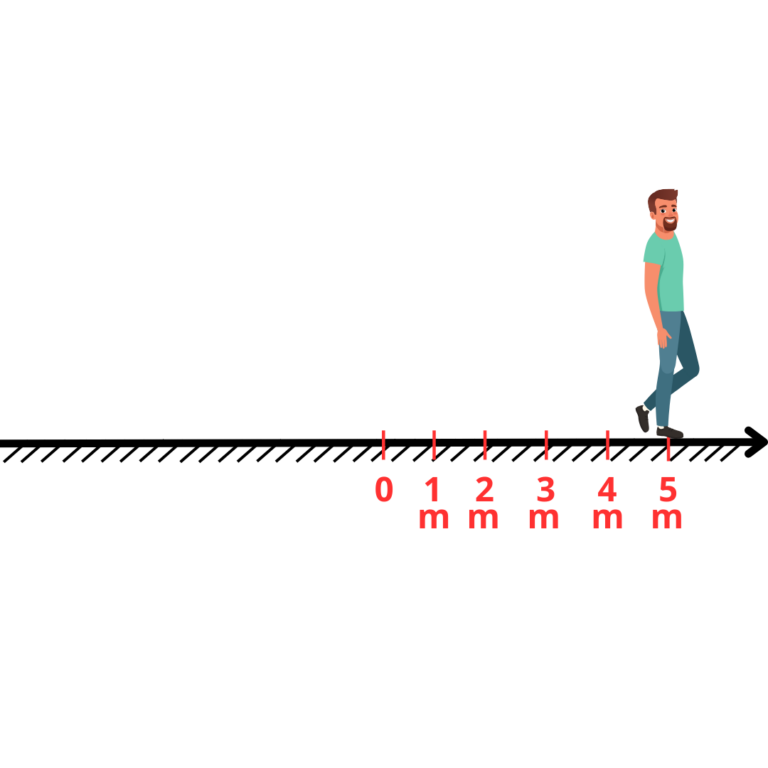
Prontinho, nessa situação, podemos dizer que a pessoa está na posição “$5$ metros” ou que ela está $5$ metros à direita da origem da trajetória (ponto $0$m). Se ele continuar andando para a direita, o valor que representa a posição dele irá aumentar, nessa situação dizemos que o corpo está indo a favor da trajetória ou no “sentido positivo da trajetória”. E o que aconteceria, nesse exemplo, se a pessoa começasse a voltar, passando para a esquerda da origem da trajetória?
Nesse caso, criaríamos marcos negativos, para indicar que ele está do lado oposto ao sentido positivo da trajetória, o que representaria uma meia volta, ou seja, ele se encontra em uma posição anterior a posição que ele estava quando começou a andar
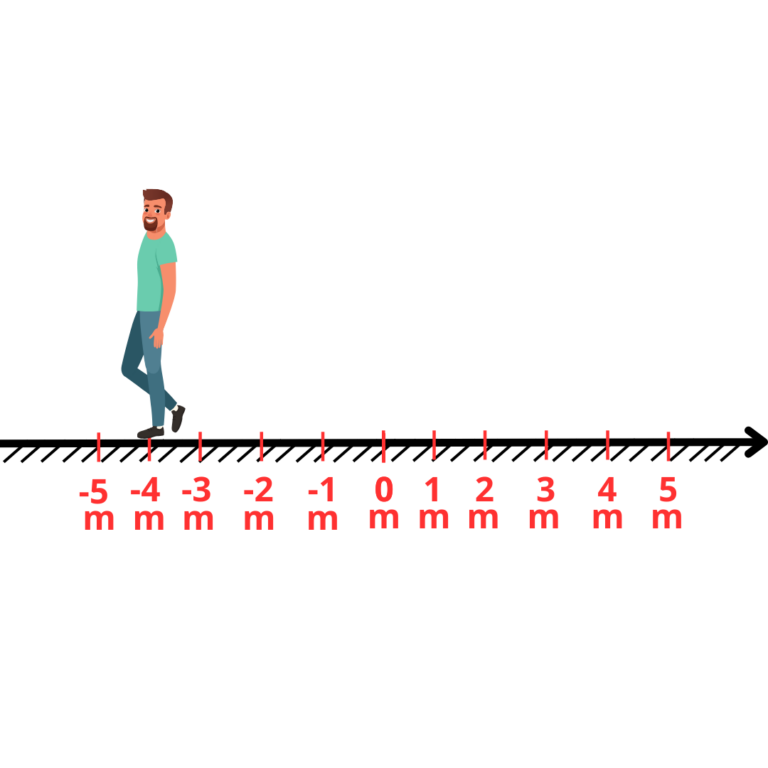
Na foto acima, podemos dizer que a pessoa está na posição “-4m”, isso significa que ela está $4$ metros à esquerda do início do percurso. Você pode se perguntar: “Mas e se a trajetória fosse considerada como sendo da direita para a esquerda?”, então os valores iriam crescer à esquerda do ponto $0$ metros e à direita dele estariam os números negativos.
O que é deslocamento?
O deslocamento pode ser descrito como o quanto um corpo se distanciou da sua posição inicial, ao final do movimento observado. Devemos ter cuidado, pois apesar de parecido, o deslocamento não é a mesma coisa que distância percorrida, uma vez que se um corpo começar seu movimento e terminar no mesmo lugar, ele não terá se deslocado nenhum milímetro sequer, porque ele não se afastou em nada da posição inicial. Podemos dizer também, que o deslocamento é a “menor distância entre dois pontos”, pontos esses que são a posição inicial e final de um corpo.
Exemplo:
Qual é o deslocamento do veículo representado na imagem abaixo?
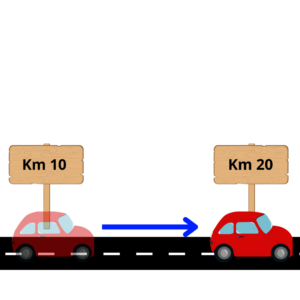
Só nos é importante a posição final e inicial do veículo, e para calcular o deslocamento ou variação do espaço, utilizamos a seguinte equação:
$$\Delta s=s_f-si$$
Ou seja, a variação ($\Delta$) do espaço é igual a posição final ($s_f$, espaço final) menos a posição inicial ($s_i$, espaço inicial). A posição em que o carro começa a trajetória é no $Km\;10$ e a finaliza no $Km/;30$, então seu deslocamento é de $20\;km$, em outras palavras, ele dista $20$ quilômetros do ponto inicial ao final do movimento
$$\Delta s=s_f-si$$
$$\Delta s=30-10=20$$
Quando o valor dessa variação dá positivo, significa que o corpo se movimentou a favor da trajetória, nesse caso dizemos que ele está em um movimento progressivo, e caso achássemos um valor negativo, teríamos um movimento retrógrado (ou regressivo), que por sua vez, significa que o corpo está indo no sentido contrário à trajetória. Agora imaginemos que o veículo dessa questão finalizasse sua trajetória no $Km\;10$, qual seria seu deslocamento? Basta calcularmos
$$\Delta s=s_f-si$$
$$\Delta s=10-10=0$$
Isso mesmo, zero, como disse antes, para a grandeza deslocamento, só nos interessa as posições em que o carro começou e terminou seu trajeto, não importando quantos quilômetros ele percorreu até chegar em seu destino (que seria a distância percorrida).
Formado em Eletrotécnica pelo IFRN, além de ter cursos de Matemática Básica e Cálculo pela empresa Help Engenharia.
