Em conjunto com as definições de deslocamento e aceleração, a velocidade é um dos conceitos mais importantes da física clássica, especificamente da cinemática (estudo dos movimentos), e nos acompanhará durante todo o estudo dessa grande área do conhecimento.
O que é velocidade?
De forma simplificada, a velocidade é a medida do quão rápido um objeto, veículo ou ser vivo percorre uma determinada distância. Agora em termos formais, a velocidade é uma grandeza vetorial (além do valor numérico, possui direção e sentido), que quantifica quanto um corpo (qualquer coisa que possua matéria) se deslocou em um intervalo de tempo limitado. Apesar disso, para situações mais simples, onde há movimento em apenas uma direção (chamados movimentos unidimensionais), tratamos a velocidade como uma grandeza escalar, onde só nos interessa seu valor numérico.
A unidade de medida padrão da velocidade, definida pelo Sistema Internacional de Unidades (SI), é “metros por segundo”, cujo símbolo é
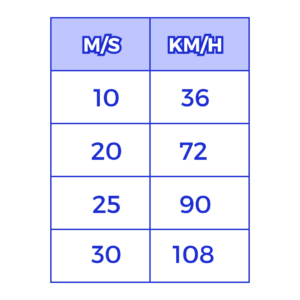
Tipos de velocidade
Podemos classificar a velocidade em dois tipos: Instantânea e média, cada uma com suas características e usadas em diferentes situações, a depender do exercício.
Velocidade instantânea:
Essa é aquela velocidade que percebemos ao olharmos para o velocímetro de um carro quando a velocidade não está mudando, ou seja, é a velocidade em que o veículo (corpo) está naquele único instante, nos ajudando a analisar o que está acontecendo em um momento específico, não refletindo a velocidade em um período um pouco mais extenso.
Velocidade média:
Calculamos a velocidade média de um corpo, ao dividirmos a distância percorrida por ele, pelo tempo que demorou para o trajeto ser finalizado.
As vezes nos são dadas as variações tanto da distância quanto do tempo, no entanto, em alguns exercícios temos apenas os espaços e instantes iniciais e finais, sendo necessário calcular as variações (delta) ao substituir na equação da velocidade média. E vale ressaltar que, na maioria dos exercícios, o tempo inicial será considerado como o instante
Exemplo 1:
Um casal planeja viajar de férias e a distância a ser percorrida até o destino é de
Temos tudo o que precisamos para calculá-la, toda a distância percorrida e o tempo, nos resta substituir na equação
Devemos sempre respeitar as unidades de medida, se a distância estava em quilômetros e o tempo em horas, a velocidade calculada deve estar em
Exemplo 2:
Um motorista foi multado por excesso de velocidade, pois estava com uma velocidade maior que a permitida no trecho, que era de
Há duas diferenças em relação ao exercício anterior, primeiramente, não temos a distância percorrida de forma explícita, tempos as posições final e inicial, e o tempo está em minutos, como a questão pede que a velocidade fique em
Exemplo 3:
Um carro percorreu
Essa questão é um pouco mais complexa, e nos exige uma certa manipulação algébrica. Para calcular a velocidade média de um veículo, precisamos da distância total percorrida e dividir pelo tempo total, então para calcularmos a velocidade média nessa questão, precisamos considerar os dois trechos e somar, suas distâncias e tempos.
Antes de substituirmos os valores, vamos converter as unidades, pois nossa resposta deve estar em
Há duas sutilezas ao trabalhamos com a velocidade média que devem ser levadas em consideração, por ser uma média, ela não nos dá informações sobre variações da velocidade durante o percurso, ou seja, um veículo pode manter uma velocidade constante o tempo todo ou variar sua velocidade, não impactando em nada o resultado que iremos calcular.
Também não podemos concluir nada sobre o deslocamento total (caso não saiba a diferença entre distância percorrida e deslocamento, confira nosso artigo sobre esse assunto), pois para o cálculo da velocidade média, nos interessa apenas a posição que o veículo começou o trajeto e a posição em que ele o finalizou, não importando ou sendo possível saber se foi feita uma pausa para abastecer ou se ele deu ré em algum momento. Essas informações são importantes, pois muitas vezes nos sentimos tentados a concluir mais coisas do que é possível ou permitido, e com isso podemos errar uma questão por falta de atenção.
Os livros geralmente diferenciam “velocidade média” de “velocidade escalar média”, sendo a primeira expressão utilizada quando consideramos a velocidade como um vetor, possuindo módulo, direção e sentido; e o segundo é para casos mais simples, onde podemos tratar a velocidade como grandeza escalar, onde o valor numérico da velocidade média já é suficiente.
Velocidade relativa
Um conceito interessante, que merece uma menção honrosa nesse artigo é o de “velocidade relativa”, que diz respeito a velocidade de um corpo em relação a outro, e há três tipos de situações que a englobam.
1) Corpos com mesma velocidade e mesmo sentido
Para simplificar o entendimento, falarei de veículos, mas essas considerações servem para qualquer tipo de corpo. Se dois carros estão rodando em uma mesma velocidade, a velocidade relativa entre eles é zero, ou seja, olhando da perspectiva (referencial) de um dos ocupantes desses carros hipotéticos, se não houvesse indicativos na pista e a paisagem fosse totalmente ignorada, um carro estaria “parado” em relação ao outro.
2) Corpos com um mesmo sentido em uma trajetória
Quando dois carros estão trafegando em um mesmo sentido, ou seja, estão indo para um mesmo lugar, e estão com velocidades diferentes, a velocidade relativa entre eles é calculada como o módulo da diferença entre suas velocidades. Então se o carro A tiver a
3) Corpos com sentido opostos em uma trajetória
Quando dois carros estão em sentidos opostos, o cálculo da velocidade relativa entre eles é feito pela soma do módulo (valor positivo) das velocidades, é por isso que uma colisão é mais brutal e “potente” quanto poderíamos pensar, pois quando veículos estão indo em sentidos opostos, caso eles colidam, as velocidades de ambos se somam, contribuindo para um impacto mais forte.
Gráfico da velocidade
Por fim, mas não menos importante, para que o artigo fique recheado de conteúdo, irei falar um pouco sobre o gráfico da velocidade em relação ao tempo. Tomemos como exemplo um veículo qualquer que possui o seguinte comportamento quanto a sua velocidade:
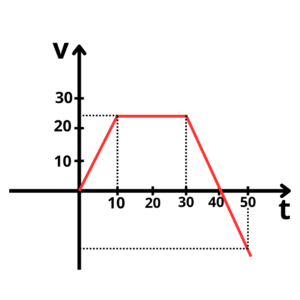
Podemos afirmar algumas coisas a partir do gráfico, no intervalo entre
Se estais lendo até aqui, parabéns, você gosta mesmo de física, e como presente, lhe darei duas dicas valiosíssimas. Caso você calcule a área embaixo de um gráfico de velocidade por tempo (como na última figura), o resultado dessa área vai ser numericamente igual ao espaço percorrido (distância percorrida). Além disso, a inclinação do gráfico nos dá indicação do quão acelerado o corpo está, quanto mais inclinado o gráfico estiver, maior sua aceleração, com o contrário também sendo verdade; e caso o gráfico forme uma reta horizontal, significa que não há inclinação, portanto, não há aceleração, trata-se de um movimento uniforme.

Formado em Eletrotécnica pelo IFRN, além de ter cursos de Matemática Básica e Cálculo pela empresa Help Engenharia.




