Capaz de solucionar diversos cálculos e uma ferramenta essencial para todo estudante, a regra de 3 é muito útil independentemente do seu grau de escolaridade e até para quem irá prestar algum concurso cujas questões de matemática possuem um nível mais tranquilo.
O que é regra de 3 simples?
É um método/dispositivo matemático que nos permite encontrar um valor ou uma quantidade de algo, com base em outros valores já conhecidos. Por exemplo, digamos que você quer contratar um pedreiro para fazer uma reforma, no entanto, tu prezas por ter privacidade e conforto e não queres que a obra dure muito tempo, o pedreiro disse que precisaria de um servente, e juntos terminariam a reforma em 12 dias, mas precisas que tudo termine em no máximo 4 dias, quantos serventes à mais precisam ser contratados para que a obra termine dentro do prazo? É esse tipo de pergunta que a regra de 3 ajuda a responder.
De um jeito formal e geral, a regra de 3 relaciona duas grandezas, a fim de facilitar a obtenção de um valor desconhecido dentre elas, mas antes de irmos para os exercícios para que possa explicar como usá-la, preciso que saibas o que é uma grandeza e outras coisas mais.
Grandezas direta e inversamente proporcionais
Em termos simples, grandeza é tudo o que podemos medir, mensurar ou contar, desde a quantidade de pães, quantos litros de água há em um garrafão, até a velocidade de um carro ou a força aplicada em uma bola de vôlei em uma cortada. E para entendermos a regra de 3 é fundamental que saibamos a diferença entre grandezas diretamente proporcionais e inversamente proporcionais, o primeiro tipo é quando ambas se comportam de forma parecida em relação a quanto elas aumentam ou diminuem.
Tomemos como exemplo uma fábrica de sorvete que possui
Agora vamos pensar em outro exemplo, suponhamos que ao percorrermos um determinado trajeto de carro a uns
Como usar a regra de 3 simples?
Há várias formas de se aplicar a regra de 3, mostrarei a que acho mais simples e que mais vejo sendo utilizada, primeiramente devemos identificar quais são as duas grandezas importantes na questão, depois analisamos se elas são direta ou inversamente proporcionais (isso mudará um pouco a forma de resolver), por fim, montaremos uma equação de
Exemplo 1:
Dedicando
Começamos identificando as grandezas, que nesse caso são o “tempo” em horas e a “quantidade de máscaras”. Em seguida, organizaremos da seguinte forma: Duas colunas, cada uma com o nome de uma grandeza, colocamos na primeira linha abaixo desses nomes a quantidade (ou valor) inicial e na linha abaixo a quantidade final, com a observação de que como a questão nos pede a quantidade de máscaras final (quando o artesão trabalhar

Então, analisamos como as grandezas se relacionam, se o artesão trabalhar mais horas, mantendo a produtividade, ele conseguirá produzir mais ou menos máscaras? Mais máscaras, pois ele tem mais tempo para produzir mais máscaras, uma vez que a produção dele não irá diminuir e mesmo que diminuísse, por ter mais tempo, a quantidade seria maior no final, portanto, elas são diretamente proporcionais, enquanto uma cresce a outra cresce também. Sabendo disso, multiplicaremos os valores em cruz os valores da tabela que montamos, como mostra a figura abaixo:
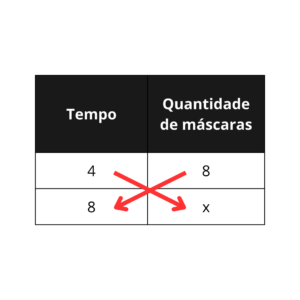
E então, igualamos as multiplicações, montando uma equação de
Para finalizar a questão, resolvemos a equação (tem artigo aqui no canal sobre ela)
O artesão confeccionará
Exemplo 2:
Um tanque de água demora
Primeiramente, vamos identificar as grandezas, só que temos que descartar uma possibilidade, o tanque não será considerado em nossos cálculos, pois apesar de ele ser uma grandeza (podemos contar a quantidade de tanques), seu valor não muda, temos um tanque no início e no final continuamos somente com ele, então, as grandezas importantes serão a “quantidade de torneiras” e o “tempo”. Agora, organizaremos a tabela do mesmo jeito que no exercício anterior, com uma coluna para a cada grandeza:
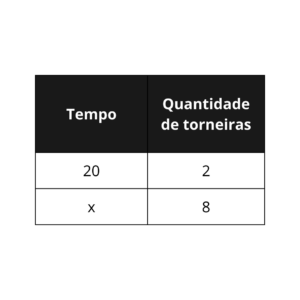
Uma vez organizada a minitabela, analisemos a proporcionalidade entre as grandezas, se aumentaram o número de torneiras, o tanque será cheio em mais ou menos tempo? Menos tempo, pois quanto mais torneiras, mais água será injetada no tanque, fazendo com que ele encha mais rápido, então, já que uma grandeza cresce, enquanto a outra diminui, elas são inversamente proporcionais. O que isso impacta na questão? Multiplicaremos os valores da primeira linha (de cima para baixo) e os da segunda linha entre si:
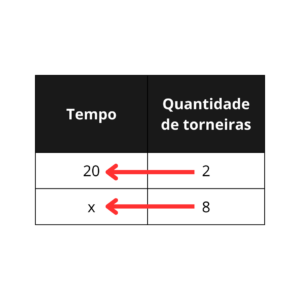
E então montamos uma equação linear igualando ambas as multiplicações
Por fim, resolvemos a equação, achando assim a resposta do exercício (lembre-se de colocar a unidade de medida correta)
Demorará
Regra de 3 composta
A extensão da regra de 3 simples é a regra de 3 composta, cujas diferenças são a quantidade de grandezas, que são
Exercícios resolvidos de regra de 3 simples
1. Um trabalhador recebe
Definir as grandezas é muito importante para acertarmos a questão, no caso acima temos as grandezas “dinheiro” e “dias”, então, podemos montar a tabela, com a incógnita no valor monetário:
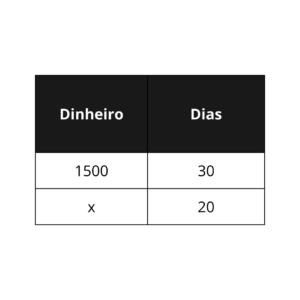
Se ele trabalhar menos dias, seu salário diminuirá, portanto, são grandezas diretamente proporcionais. Multipliquemos então em cruz os valores da tabela
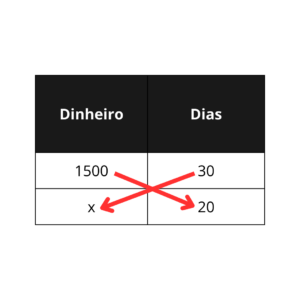
Montamos a equação e a resolvemos
O trabalhador receberá mil reais se trabalhar por
2. Um embalador consegue completar
As grandezas nessa segunda questão são “caixas” e “tempo”, mas temos que nos atentar a um detalhe, em todos as outras situações abordadas no artigo, as unidades das grandezas eram as mesmas, só que nessa questão temos o tempo em horas e em minutos, precisamos deixá-los com a mesma unidade antes de montarmos a tabela. Por comodidade irei transformar minutos para horas, mas caso a questão pedisse o tempo em minutos ao invés da quantidade de caixas, precisaria ser feita a conversão contrária. Basta dividir a quantidade de minutos por
Agora podemos montar a tabela
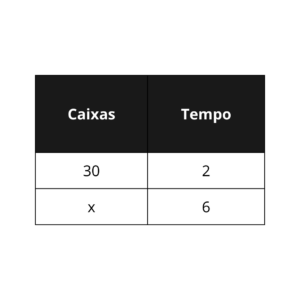
Se em certo tempo o embalador finaliza
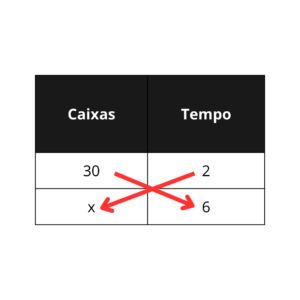
Enfim, resolvemos a equação
Serão embaladas
3. Uma família nas férias costuma demorar
As grandezas dessa vez são “tempo” e “velocidade”, dessa vez o segundo valor de tempo está implícito, mas é possível deduzi-lo facilmente, a metade de algo significa esse algo dividido por
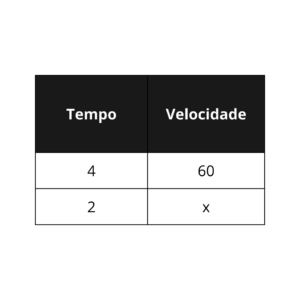
Já que o percurso deve ser finalizado em menor tempo, a velocidade do carro deve aumentar, ou seja, as grandezas são inversamente proporcionais, teremos que multiplicar os valores das respectivas linhas, não de forma cruzada
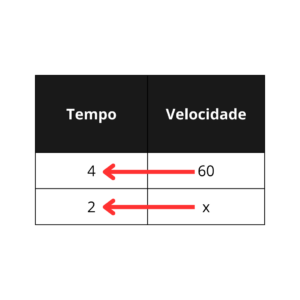
E como sempre, resolvemos a equação
Como a questão não especificou a unidade de medida, mantemos ela como sendo quilômetros por hora, portanto, o carro deve manter a velocidade de

Formado em Eletrotécnica pelo IFRN, além de ter cursos de Matemática Básica e Cálculo pela empresa Help Engenharia.




