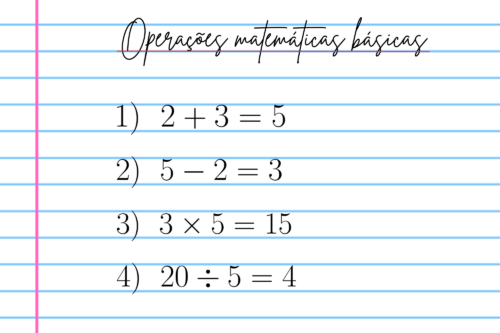Primeiramente, o que é uma operação matemática? Em poucas palavras, são processos que realizamos com números (que representam quantidades de algo) e seguem uma lógica bem definida. Existem quatro fundamentais, que nos permite estudar e trabalhar com todos os outros assuntos. São elas a adição, subtração, multiplicação e divisão, e cada uma possui características e propriedades específicas. Dominar essas operações é essencial para resolver problemas mais complexos e entender outros conceitos matemáticos.
Revisão de números reais e inteiros
Antes de abordarmos as operações, precisamos revisar alguns conceitos de conjuntos numéricos. Para fazermos cálculos da matemática básica, os números inteiros são essenciais, eles incluem todos os números negativos, o zero e números positivos.
Já os números reais englobam todos os números inteiros, além de frações e decimais, permitindo uma maior variedade e precisão nos cálculos. Eles são representados pela letra $\mathbb{R}$ e incluem números naturais, inteiros, racionais e irracionais. Os números reais são indispensáveis para medidas e cálculos mais complexos, como em geometria e álgebra.
Adição
Conhecida também como soma, envolve juntar dois ou mais números (que na adição são chamados de parcelas) para obter um valor maior. Por exemplo, ao adicionarmos $3$ e $5$, obtemos $8$. Ela é representada pelo símbolo $+$
Exemplos:
1) $2+2=4$
2) $1+3+5=9$
3) $5+2+6+5=18$
Propriedades da adição:
As principais propriedades da adição incluem a comutatividade (a ordem dos números não altera o resultado) e a associatividade (a forma de agrupar os números não muda a soma). E caso não saiba o que é uma propriedade, basicamente, é um certo padrão que se aplica na maioria ou em todos os casos.
Exemplo de comutatividade:
$$2+3+1=2+1+3=1+2+3=6$$
Independentemente da ordem dos números, o resultado do cálculo não se altera
Exemplo de associatividade:
$$(4+5)+2=4+(5+2)=11$$
Se todas as parcelas estiverem se somando, não importa como são agrupados os números, o resultado será o mesmo
Subtração
A subtração, ou diferença, envolve retirar uma quantidade de um número. Subtraindo $3$ unidades de $8$, chegamos a $5$. Ela é representada pelo símbolo $-$
Exemplos:
1) $8-6=2$
2) $10-3-4=3$
3) $8-4+7-3=8$
Toda subtração pode ser considerada uma soma, pois se analisar os sinais, o cálculo não se altera e o resultado continua o mesmo (tem artigo aqui no blog sobre análise de sinais). E diferentemente da soma, a subtração não é comutativa ou associativa, podemos visualizar isso ao tentarmos subtrair $3$ de $10$, cujo resultado vai ser $7$, agora se subtrairmos $10$ de $3$, o resultado será $-7$.
Elemento neutros e números opostos
Na adição (e na subtração), o elemento neutro é $0$, porque qualquer número adicionado (ou subtraído) a $0$ permanece o mesmo, por exemplo: $6+0=6$ ou $5-0=5$. Há um conceito importante, chamado elemento oposto ou “número oposto”, que são números de sinais diferentes, que caso sejam somados o resultado dá zero, por exemplo, o oposto de $7$ é $-7$, pois $7+(-7)=0$ (o conceito de número oposto só se aplica na soma e subtração). Saber esses conceitos ajuda a simplificar cálculos e a resolver problemas mais rapidamente.
Multiplicação
Também chamado de produto, nada mais é do que várias somas de um mesmo número (chamado de fator na multiplicação). Por exemplo, $4$ multiplicado (ou quatro vezes) por $3$ é o mesmo que somar $4$ três vezes $(4+4+4)$, resultando em $12$. O número $1$ é conhecido como o elemento neutro da multiplicação, pois qualquer número multiplicado por $1$ permanece inalterado. Ela é representada pelo símbolo $\times$ (ou por um pontinho, exemplo: $4.3=12$)
Exemplos:
1) $2\times3=3+3=6$
2) $10\times1=10$
3) $4\times(-2)=-2+(-2)+ (-2)+ (-2)=-2-2-2-2=-8$
Propriedades da multiplicação:
A multiplicação também é comutativa e associativa, facilitando bastante os cálculos. Além disso, existe a propriedade do elemento neutro (multiplicar por $1$ não altera o valor). É importante entender as propriedades, pois deixa mais prática a manipulação dos fatores.
Exemplo de comutatividade:
$$4\times5\times2=5\times2\times4=40$$
Exemplo de associatividade:
$$2\times(3\times6)=(2\times3)\times6=36$$
Há também a propriedade distributiva da multiplicação, que se aplica quando temos um número, multiplicando um parênteses que contém uma soma ou subtração de dois ou mais números (podem ser letras também). Ela consiste em distribuir a multiplicação desse número por todos os termos dentro do parênteses, em outras palavras, ele irá multiplicar todo mundo.
Exemplos:
1) $2\times(3+4)=2\times3+2\times4=6+8=14$
2) $-1\times(1+2-3)=-1\times1+(-1)\times2+(-1)\times(-3)=-1-2+3=0$
3) $3\times(x-2)=3\times x+3\times(-2)=3x-6$
Divisão
Muitas vezes chamada de quociente, é uma operação que nos permite separar um valor em partes iguais. Se temos a divisão entre $12$ e $3$, estamos implicitamente perguntando quantas unidades teremos se dividirmos $12$ em $3$ partes iguais, e o resultado é $4$. Assim como na multiplicação, o elemento neutro da divisão é o número $1$, pois dividir qualquer número por $1$ não altera em nada o valor. Ela é representada pelo símbolo $\div$ (ou por uma fração, exemplo: $\frac{4}{2}=2$)
Exemplos:
1) $6\div3=2$
2) $10\div2=5$
3) $25\div1=25$
Caso a divisão não resulte em um número inteiro, dizemos que o que sobrou (o que não pôde ser dividido) é o resto da divisão, mas para facilitar os cálculos, utilizaremos nesse artigo apenas divisões exatas (que resultam em números inteiros).
Exercícios resolvidos de operações matemáticas básicas
1. Numa pequena fábrica de laticínios, foi anotada a quantidade de garrafas de leite produzidas nos três primeiros dias da semana
Segunda: $80$ garrafas
Terça: $70$ garrafas
Quarta: $100$ garrafas
Quantas garrafas de leite foram produzidas ao todo?
Quando a questão nos dá vários valores e nos pede o valor total, significa que precisamos soma-los. Nesse caso, precisamos somar as garrafas que foram produzidas em cada dia
$$80+70+100=250$$
Ou seja, foram produzidas um total de $250$ garrafas
2. Um senhor chamado José, quer calcular quanto vai restar em sua conta, após pagar sua dívida em um supermercado. Sabendo que o saldo bancário dele é de $2000$ reais e que ele está devendo $700$, quanto lhe restará após quitar a dívida?
Sempre que for citado o nome dívida, déficit ou diferença, significa que há uma subtração a ser feita. Na questão acima, precisamos subtrair o valor que será usado para pagar a dívida, do valor que está na conta bancária
$$2000-700=1300$$
O senhor José ainda terá $1300$ reais, após pagar o que deve
3. Lúcia quer comprar um guarda-roupas, mas não possui todo o valor para pagar à vista, só que está acontecendo uma promoção que qualquer produto acima de $2000$ reais, pode ser parcelado em até $12$ vezes sem juros. Sabendo que cada parcela do guarda-roupas é $300$ reais, quanto ele custa?
Quando temos o valor de uma unidade de algo e é solicitado o valor de várias unidades dessa mesma coisa, significa que precisamos fazer múltiplas somas, ou seja, realizar uma multiplicação. Se cada parcela é $300$ reais e ao todo são $12$ parcelas, precisamos multiplicar $300$ por $12$ para sabermos o valor do guarda-roupas
$$300\times12=3600$$
O móvel que a Lúcia quer comprar, custa $3600$ reais.
4. Um jovem chamado Allef quer se desvencilhar de sua coleção de cartinhas, pois precisa juntar dinheiro para comprar um vídeo game. Ele tem três amigos que também colecionam, e para não desagradar ninguém, quer distribui-las igualmente entre eles. Sabendo que sua coleção contém $180$ cartas, com quantas cada um de seus amigos irá ficar?
Temos um valor, que será distribuído em quantidades iguais, isso te lembra algo? Toda vez que for dito que alguma coisa será distribuída (ou dividida), significa que teremos que realizar uma divisão. Nesse caso, precisamos dividir a quantidade de cartinhas pelo número de amigos
$$180\div3=60$$
Portanto, cada amigo ficará com $60$ novas cartas em sua coleção.
Importância de aprender as operações matemáticas básicas
Durante toda sua jornada acadêmica na matemática, você irá precisar realizar operações básicas, então é indispensável entender bem elas. Essas operações, juntamente com os assuntos de frações e expressões matemáticas, são a base da matemática básica, sem um entendimento completo dessas operações, enfrentamos dificuldades em assuntos como álgebra e cálculos mais complicados. Além disso, elas nos ajudam a resolver problemas do dia a dia, como calcular troco, estimar gastos e dividir contas.
Formado em Eletrotécnica pelo IFRN, além de ter cursos de Matemática Básica e Cálculo pela empresa Help Engenharia.
