O Teorema de Ptolomeu é um resultado clássico da geometria euclidiana que descreve uma relação fundamental entre os lados e as diagonais de um quadrilátero inscrito em uma circunferência, ou seja, um quadrilátero cujos quatro vértices estão localizados exatamente sobre o contorno de uma circunferência. Nomeado em homenagem a Claudius Ptolomeu, um proeminente matemático e astrônomo da antiguidade, este teorema desempenhou um papel crucial no desenvolvimento da trigonometria e continua a ser amplamente utilizado em problemas de geometria plana. Neste artigo, apresentaremos a formulação do Teorema de Ptolomeu, acompanhada de exemplos e aplicações que ilustram sua relevância e elegância.
Enunciado do Teorema de Ptolomeu
Seja $ABCD$ um quadrilátero inscrito em uma circunferência, com os vértices $A$, $B$, $C$ e $D$ dispostos nesta ordem, conforme mostrado na figura.
O Teorema de Ptolomeu afirma que:
$$ AC \cdot BD = AB \cdot CD + AD \cdot BC. $$
Em palavras, o Teorema de Ptolomeu afirma que, em um quadrilátero inscrito em uma circunferência, o produto dos comprimentos das diagonais é igual à soma dos produtos dos comprimentos de seus pares de lados opostos.
Exemplos de aplicações
O primeiro exemplo de aplicação é um caso clássico que demonstra como o teorema pode ser utilizado.
Exemplo 1: Considere um quadrilátero $ABCD$ inscrito em uma circunferência, onde os comprimentos dos lados e das diagonais são dados por: $AB = 8 \ m$, $BC = 7 \ m$, $ CD = 5 \ m$, $AD = 6 \ m$, $BD = 10 \ m$, conforme a figura:
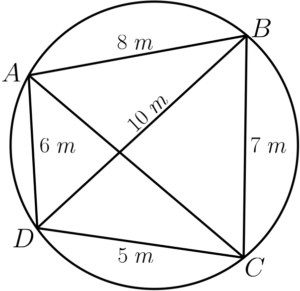
Determine o comprimento da diagonal $AC$.
Solução: De acordo com o Teorema de Ptolomeu:
$$AC \cdot BD = AB \cdot CD + AD \cdot BC. $$ Substituímos os valores conhecidos, temos:
$$ AC \cdot 10 = 8 \cdot 5 + 6 \cdot 7$$
$$ AC \cdot 10 = 40 + 42 $$
$$ AC \cdot 10 = 82. $$
Dividindo ambos os lados por $10$, obtemos:
$$ AC = 8,2 \ m.$$
Portanto, o comprimento da diagonal $AC$ é $8,2 \ m$.
Essa segunda aplicação ilustra como o teorema pode ser utilizado em problemas de nível olímpico.
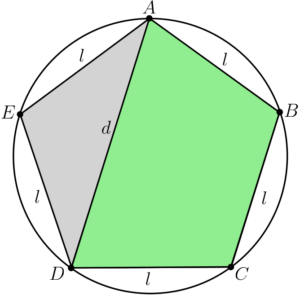
Exemplo 2: Prove que, em um pentágono regular, a razão entre a diagonal $d$ e o lado $l$ é um número irracional. Além disso, determine qual é esse número irracional.
Solução: Considere um pentágono regular $ABCDE$ de lado $l$ inscrito em uma circunferência.
Traçamos a diagonal $AD$, que chamaremos de $d$, formando o quadrilátero $ABCD$, destacado em verde na figura.
Agora, considere as diagonais $AC$ e $BD$. Como a figura é um pentágono regular, todas as diagonais têm o mesmo comprimento. Assim, $AC = BD = d$.
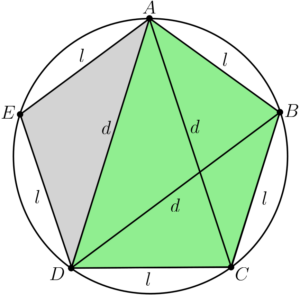
Aplicando o teorema de Ptolomeu ao quadrilátero $ABCD$, obtemos:
$$d \cdot d=l \cdot d + l \cdot l$$
$$d^2=ld+l^2$$
$$d^2-ld-l^2=0$$
Estamos diante de uma equação quadrática. Utilizando a fórmula de Bhaskara para encontrar $d$:
$$d=\frac{-(-l)\pm\sqrt{(-l)^2-4\cdot 1\cdot-l^2}}{2}$$
$$d =\frac{l\pm \sqrt{l^2+4l^2}}{2}$$
Colocando $l^2$ em evidência e utilizando propriedades de radiciação, temos:
$$d=\frac{l\pm \sqrt{l^2(1+4)}}{2}=\frac{l\pm \sqrt{l^2}\sqrt{5}}{2}$$
$$d=\frac{l\pm l\sqrt{5}}{2}$$
Como o problema pede a razão entre $d$ e $l$, dividindo ambos os lados da equação por $l$:
$$ \frac{d}{l}=\frac{\frac{l\pm l\sqrt{5}}{2}}{l}$$
Resolvendo a divisão de frações e simplificando, obtemos:
$$\frac{d}{l}=\frac{l\pm l\sqrt{5}}{2l}$$
Colocando $l$ em evidência no numerador:
$$\frac{d}{l}=\frac{l(1\pm \sqrt{5})}{2l} $$
Simplificando, encontramos a seguinte expressão:
$$\frac{d}{l}=\frac{1\pm\sqrt{5}}{2}$$
Temos duas soluções, mas note que $1 < \sqrt{5}$, logo
$$ \frac{1-\sqrt{5}}{2}$$
É negativa e, portanto, inválida para medidas de comprimento. Assim, a razão entre a diagonal $d$ e o lado $l$ é a solução positiva:
$$\frac{d}{l}=\frac{1+\sqrt{5}}{2}.$$
O resultado encontrado é o famoso número de ouro, um número irracional que é muito presente na matemática.
Licenciado em Matemática pela UEPB.
