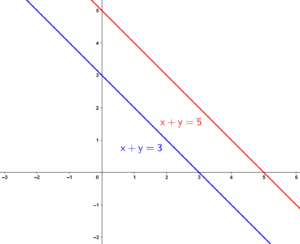
Neste artigo, falarei sobre os sistemas de equações lineares, fundamentais na matemática, e como resolvê-los por diferentes métodos, como substituição, comparação, adição ou subtração, além de técnicas avançadas como a regra de Cramer e o escalonamento. Por meio de exemplos e exercícios resolvidos, mostrarei como aplicar esses métodos para encontrar as soluções dos sistemas.
O que é um sistema de equações?
Um sistema de equações é um conjunto de duas ou mais equações que compartilham as mesmas variáveis. O objetivo ao resolver um sistema é encontrar os valores dessas variáveis que tornam todas as equações do sistema verdadeiras simultaneamente. Os sistemas de equações podem ser lineares ou não lineares, dependendo do tipo das equações envolvidas.
Exemplos de sistemas de equações:
1)
2)
3)
Tipos de sistemas de equação
Podemos separar os sistemas de equação em três tipos, de acordo com o grau das incógnitas (letras) e número de equações e incógnitas.
Sistema linear:
Denominamos de lineares os sistemas que possuem apenas equações com variáveis de grau
Exemplos de sistemas lineares:
1)
2)
3)
Sistema não linear:
Se houver ao menos uma variável com grau
Exemplos de sistemas não lineares:
1)
2)
3)
Sistemas quadrados:
Sistemas quadrados são os que possuem o mesmo número de equações e incógnitas, e essa denominação vale independentemente se o sistema é linear ou não.
Exemplos de sistemas quadrados:
1)
2)
3)
Geralmente nos referimos a sistemas quadrados com a mesma nomenclatura que usamos em relação a matrizes quadradas. Chamamos um sistema com duas equações e duas variáveis de “sistema
Como resolver um sistema de equações?
A resolução de um sistema de equações pode ser feita por diferentes métodos, dependendo do tipo do sistema e da quantidade de equações e incógnitas. Entre os métodos mais comuns, estão o da substituição, comparação, adição ou subtração, e especificamente para sistemas quadrados, podemos utilizar a regra de Cramer e o escalonamento. Irei explicar cada um desses métodos de resolução a seguir.
Mas antes, falarei algo de extrema importância, só podemos resolver um sistema de equações, se ele possuir um número de equações igual ou maior que o número de variáveis, caso tenhamos mais letras que equações, não conseguiremos resolver o sistema.
Método da substituição:
No método da substituição, escolhemos uma das equações e isolamos uma das variáveis. Depois, substituímos essa expressão na outra(s) equação(s), obtendo uma equação com apenas uma incógnita. Resolvendo essa equação, podemos substituir o valor encontrado na equação original para determinar as outras variáveis. A depender se temos três ou mais variáveis, esse processo pode ter que ser feito repetidas vezes, ou se for um sistema mais simples, onde uma das equações possui uma variável, é possível resolver facilmente por esse método.
Exemplo: Resolva o sistema de equações abaixo
Primeiramente, escolhemos a variável que iremos isolar. Escolherei o
Agora, substituímos o
Em seguida, inserimos esse valor de
Se você quiser ter certeza de que acertou, ou se seu professor pedir que prove que as soluções são válidas para o sistema, deves substituir os valores encontrados em ambas as equações, caso as igualdades se tornem verdadeiras, as respostas encontradas serão solução do sistema
A primeira deu certo, vamos verificar a outra
Método da comparação:
Esse método, que é mais utilizado em sistemas com duas equações, consiste em isolarmos uma mesma variável e igualarmos as expressões, a fim de a eliminarmos do sistema, restando apenas uma equação simples com uma variável. Depois que acharmos o valor numérico dessa incógnita que sobrou, substituímos em uma das equações para obter o valor da outra e assim resolvermos o sistema.
Exemplo: Ache, se houver, a solução do sistema linear abaixo
Pouco usual, a técnica da comparação é basicamente o método da substituição utilizado duas vezes. Ela consiste em isolarmos a mesma variável em todas as equações, e igualamos os resultados, a fim de termos uma única equação com uma incógnita (ou seja, simplificarmos o sistema)
1° equação:
2° equação:
Então, igualamos os resultados e tentamos encontrar o valor de
Quando chegamos em zero igual à zero, significa que o sistema não possui apenas uma solução, mas infinitas. No final do artigo explicarei o nome para cada tipo de sistema de acordo com o número de soluções possível. Aconselho utilizar o método da substituição ao invés desse, mas fica a critério do leitor, caso ache mais simples
Método da adição ou subtração:
O método da adição ou subtração (também conhecido como método da eliminação) é utilizado quando é possível somar ou subtrair as equações de forma a eliminar uma das variáveis. Isso pode ser feito se os coeficientes de uma das variáveis forem opostos. Após eliminar uma variável, basta resolver a equação resultante e substituir o valor obtido nas demais equações.
Exemplo: Encontre a solução para o sistema:
Nesse terceiro método, alinhamos as equações com seus termos correspondentes na mesma ordem (
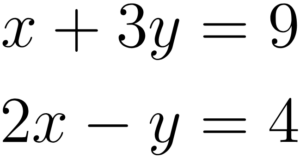
Traçamos uma linha horizontal logo abaixo das equações
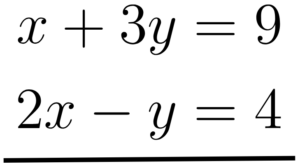
Em seguida, manipulamos uma das equações de forma a elas ficarem com um dos termos literais com sinais opostos e mesmo coeficiente. Fazemos isso para quando somarmos as equações (juntarmos elas), eliminemos uma das variáveis. Nessa questão irei eliminar o

Por fim, realizamos a soma das equações, operacionalizando os termos semelhantes
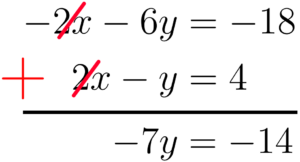
Restando assim, apenas uma simples equação de primeiro grau para ser resolvida
Substituímos o valor de
Para finalizar a questão, verificamos substituindo nas equações originais
1° equação:
2° equação:
Resolução de sistema pela regra de Cramer:
A regra de Cramer é uma técnica usada para resolver sistemas lineares quadrados, ou seja, sistemas em que o número de equações é igual ao número de incógnitas. Primeiramente, montamos uma matriz com três linhas e três colunas, cujos elementos serão os coeficientes das variáveis, no entanto, precisamos organizar as equações de tal forma que fiquem todas com a mesma ordem de variáveis, além dos termos literais ficarem isolados de um lado e as constantes do outro (parece confuso, mas irei resolver uma questão e será mais fácil a visualização). Em seguida, substituímos os elementos da coluna referente a variável a qual queremos descobrir o valor, pelas constantes, em seguida dividimos o determinante dessa nova matriz, pelo determinante da matriz original, obtendo-se assim o valor numérico da variável escolhida; repetimos o processo para as demais e resolvemos o sistema.
Exemplo: Resolva o seguinte sistema linear:
Para começarmos a resolver, alinhamos os termos que possuem a mesma letra em todas as equações, no exemplo acima isso já está feito, portanto, partiremos para o passo seguinte, que consiste em montarmos uma matriz
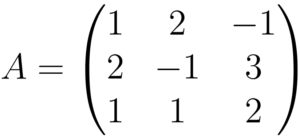
Agora colocamos a matriz com a notação de determinante
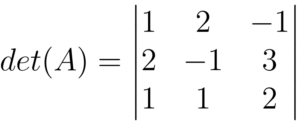
Em seguida, duplicamos as duas primeiras colunas
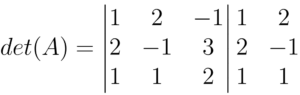
Multiplicamos os termos das diagonais principais (que estarão em vermelho na próxima foto) e repetimos o processo para as diagonais secundárias
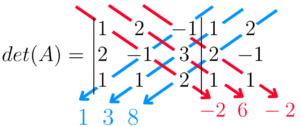
Por fim, somamos os resultados das multiplicações dos termos das diagonais principais e tiramos do valor resultante, a soma dos produtos das diagonais secundárias
Temos o determinante da matriz “original”, agora precisamos montar outras três matrizes e repetir o processo que acabamos de fazer. Para montar a primeira matriz, substituímos os elementos da primeira coluna (da esquerda para a direita), pelas constantes as quais cada equação está igualada no sistema:
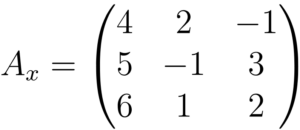
Chamei de
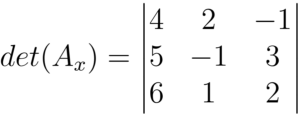
Duplicamos as duas primeiras colunas
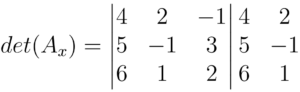
Agora realizamos o produto das diagonais principais e secundárias
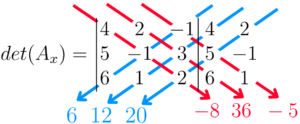
Para finalizar, somamos os resultados das multiplicações das diagonais principais e secundárias, e então subtraímos um do outro (o valor resultante das principais menos da secundária
Repetiremos o processo mais duas vezes, agora criaremos a segunda matriz, substituindo a coluna dos coeficientes das variáveis
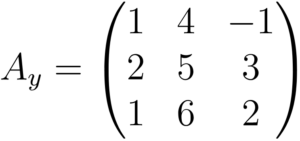
Montamos o determinante
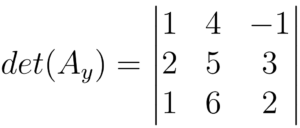
Criamos mais duas colunas que são cópias das primeiras
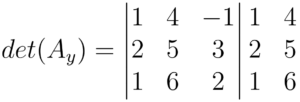
E fazemos todo aquele processo que já foi executado duas vezes
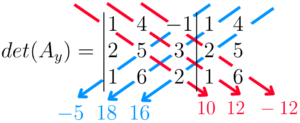
Calculamos o determinante ao subtraímos os valores resultantes das somas dos produtos das diagonais
Só nos resta calcular o determinante da matriz
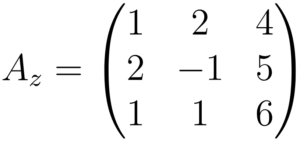
Deixamos na notação de determinante
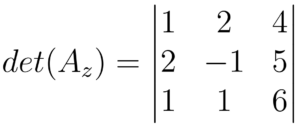
Duplicamos as primeiras duas colunas
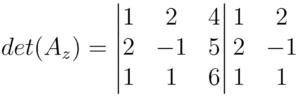
Como feito anteriormente, realizamos o produto dos termos das diagonais
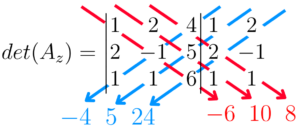
E finalizamos achando o valor do determinante da matriz
Uma vez calculados os determinantes, para encontrarmos o valor das variáveis e resolvermos o sistema, dividimos os determinantes correspondentes a cada uma das incógnitas pelo determinante da matriz
Valor de
Valor de
Valor de
Para conferirmos se acertamos, substituímos os valores nas equações (eu sei, é cansativo e longo o processo, mas o próximo método será mais simples e rápido). Para facilitar os cálculos, ao invés de utilizar a resposta simplificada para
Primeira equação:
Segunda equação:
Terceira equação:
Esse método é mais utilizado em sistemas
Método do escalonamento:
O método do escalonamento é um processo de manipulação das equações para transformá-las em uma forma mais simples, envolvendo uma série de operações básicas de forma a deixar as equações com uma quantidade crescente de incógnitas, com uma delas tendo apenas uma. Uma vez que deixarmos os sistemas nesse formato, podemos isolar a variável na menor equação e com o resultado substituir na que tem uma variável à mais e repetir o processo até todas as variáveis serem encontradas. Utilizarei a questão do exemplo anterior para efeito de comparação dos métodos
Exemplo: Resolva o sistema
A princípio, o processo de escalonar irá parecer complicado, mas com a prática ficará mais fácil e poupará tempo, em comparação a regra de Cramer. Começamos montando uma matriz
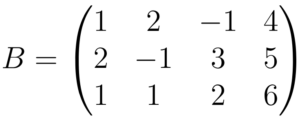
Para identificamos bem quem são as constantes, podemos passar uma linha tracejada na matriz, isolando a quarta coluna
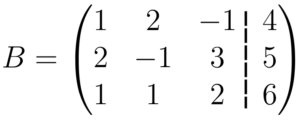
O escalonamento, como já mencionado, tem como objetivo simplificarmos as equações do sistema, de forma a conseguimos resolver uma delas e com a resposta resolver a outra e assim por diante, e para fazemos isso, temos que realizar operações de adição ou subtração entre as equações, visando eliminarmos termos com variáveis, para no final termos uma equação com uma variável, outra com duas e a terceira permanecer com as três incógnitas. Poderíamos fazer de forma mais manual e um pouco menos intuitiva, que é utilizando as equações do jeito que estão no sistema, ou utilizarmos apenas os coeficientes nos cálculos (que é da forma que irei fazer), facilitando as contas.
Após montarmos matriz, fixamos a primeira linha da matriz (não necessariamente precisa ser a primeira, mas de preferência a que for mais simples, ou seja, a que tiver coeficientes menores, como
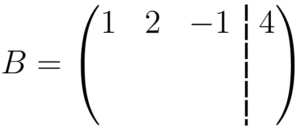
O que precisamos fazer em seguida é zerarmos os elementos que estão abaixo do
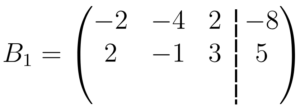
Somamos então, os elementos que estão abaixo um do outro, e com os resultados dessa soma, preenchemos a terceira linha da matriz
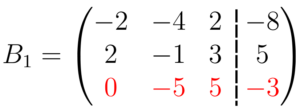
Essa linha resultante da soma das outras duas será a nova segunda linha da matriz
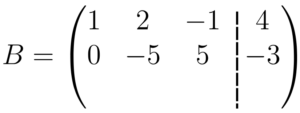
Mas afinal, o que acabamos de fazer? Simplificamos a segunda equação do sistema, ou melhor, substituímos ela por uma mais simples, com uma variável à menos. Cada um dos elementos de uma linha dessa matriz, representa, respectivamente, os coeficientes de
Repetimos esse mesmo processo, só que com a primeira e terceira linha da matriz
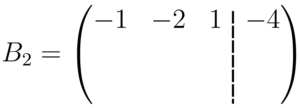
A segunda linha da matriz
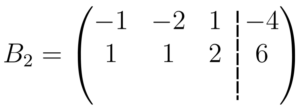
Agora somamos os elementos que estão na mesma coluna e colocamos o resultado nos espaços faltantes da matriz
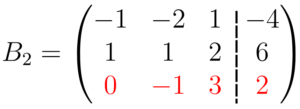
Substituímos então, essa linha resultante na matriz principal (matriz
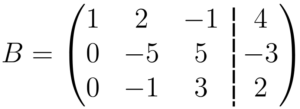
Falta pouco para terminarmos, agora não mais precisaremos de matrizes auxiliares, trabalharemos apenas com a matriz
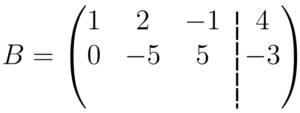
Nosso objetivo é zerar o elemento da segunda coluna da terceira linha, ou seja, o que está abaixo do
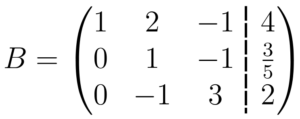
Para finalizar o escalonamento, somamos a segunda e terceira linha da matriz
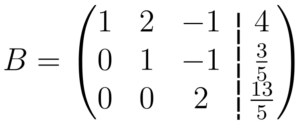
Por fim, transformamos cada linha em equação, montando assim um sistema escalonado, onde as equações estão simplificadas, e então resolvemos as equações
Começamos pela equação mais simples (a com menor número de variáveis)
Substituímos o valor encontrado na variável
Por fim, substituímos as respostas para
Achamos exatamente as mesmas respostas que utilizando o método de Cramer, só que por outro caminho.
Como classificar um sistema linear
Um sistema linear pode ser classificado em três tipos principais:
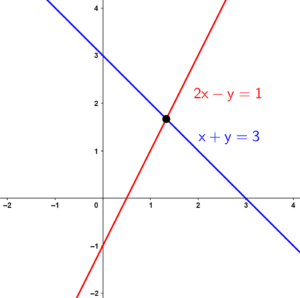
Sistema possível e determinado (SPD):
Quando há exatamente uma solução. Graficamente, a solução desse sistema é representada por retas concorrentes (que se intersectam em um único ponto)
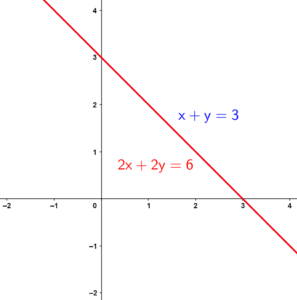
Sistema possível e indeterminado (SPI):
Quando há infinitas soluções. Graficamente, a solução desse sistema é representada por retas coincidentes (que se intersectam em infinitos pontos, ou seja, retas que são sobrepostas)
Sistema impossível (SI):
Quando não há solução. Graficamente, a solução desse sistema é representada por retas paralelas (que nunca se intersectam)