Inúmeros alunos em todo o mundo possuem dificuldade em realizar cálculos com frações, mas apesar de parecerem complicadas, elas são simples e são bem mais fáceis de se trabalhar do que com números decimais.
O que é uma fração?
É uma representação matemática de uma divisão entre dois números inteiros, mas é utilizada também para simbolizar partes de um todo.
Na barra de chocolate acima, foram comidos $2$ quadradinhos de um total de $6$ (dois sextos), então podemos representar o número de quadradinhos comidos pelo número total que a barra possuía por uma fração:
$$\frac{2}{6}$$
Mas caso queiramos representar a quantidade de quadradinhos que restaram, em relação ao total, conseguimos montar outra fração:
$$\frac{4}{6}$$
Portanto, temos quatro sextos da barra representados em forma de fração.
Caso a barra de chocolate estivesse completa, ainda poderíamos representá-la em forma de fração:
Temos $6$ quadradinhos de um total de $6$, portanto, temos seis sextos de uma barra de chocolate:
$$\frac{6}{6}$$
Que é a mesma coisa que uma barra completa de chocolate, então podemos reescrever a fração dessa forma:
$$\frac{6}{6}=1$$
Exemplos de divisões utilizando frações:
1)
$$\frac{2}{3}$$
2)
$$-\frac{7}{3}$$
3)
$$\frac{3}{\frac{1}{2}}$$
4)
$$\frac{\frac{-5}{3}}{4}$$
A forma geral da fração é:
$$\frac{a}{b}$$
O $a$ é chamado de numerador, já o $b$ é o denominador e obrigatoriamente, o $b$ deve ser diferente de zero, pois não existe divisão por zero. O número que fica em cima da fração é o que está sendo dividido (dividendo) e o que fica em baixo é o divisor, ou seja, quem divide.
O termo “razão” é sinônimo de fração, e quando for necessário representar uma proporção entre dois valores, também estaremos trabalhando de fração.
Operações com frações
Podemos realizar vários tipos de operações com frações, no entanto, irei me ater as operações básicas, que são a soma, subtração, multiplicação e divisão de frações.
Soma e subtração de frações:
Somar e subtrair frações pode ser muito simples ou um pouco trabalhoso, tudo vai depender se os denominadores (parte de baixo da fração) são iguais ou diferentes.
Frações com denominadores iguais:
Caso tenhamos frações com denominadores iguais, basta repeti-lo e somarmos (ou subtrairmos) os números que estão nos numeradores das frações.
Exemplo 1:
Resolva a operação abaixo:
$$\frac{4}{6}+\frac{2}{6}$$
Note que a parte de baixo de ambas as frações são iguais, em outras palavras, possuem o mesmo número, então, para resolver essa soma, repetimos o denominador e somamos os numeradores
$$\frac{4}{6}+\frac{2}{6}=\frac{4+2}{6}=\frac{6}{6}=1$$
Podemos barras de chocolate para entender o cálculo acima (para frações mais simples e com números positivos, utilizar pizzas ou chocolates pode ser útil para entender melhor, no entanto, para os demais casos, não é possível representá-los dessa forma), temos quatro quadradinhos de uma barra, que ao todo possuía seis quadradinhos
E queremos somar isso com dois quadradinhos restantes, que foram separados da barra para serem comidos
Juntando todos, teremos a barra inteira, com todos os seus seis quadradinhos
Exemplo 2:
Resolva a operação abaixo:
$$\frac{3}{5}-\frac{6}{5}$$
Temos uma subtração de frações com denominadores iguais, o processo será o mesmo que na soma, mantemos o denominador e subtraímos os numeradores
$$\frac{3}{5}-\frac{6}{5}=\frac{3-6}{5}=-\frac{3}{5}$$
Chegamos na resposta, mas eis a pergunta de um milhão de reais, colocamos o sinal de negativo rente (alinhado) ao traço da fração?
$$-\frac{3}{5}$$
Colocamos ele no número de cima?
$$\frac{-3}{5}$$
Ou no número debaixo?
$$\frac{3}{-5}$$
A resposta correta é: Do jeito que achares melhor. Com certeza irritei alguns matemáticos com essa resposta, porque teoricamente, o sinal rente ao traço da fração é a forma certa de se representar o sinal negativo de uma fração, mas na prática, isso não irá tornará a fração “errada” (não cometeremos um crime matemático). E colocar o sinal negativo no numerador ou denominador, pode lhe ajudar com questões de física, pois para uma fração ser negativa, um dos valores tem que ser negativo, o de cima, ou o de baixo, só que em questões envolvendo tempo, não poderíamos representar ele com sinal negativo, pois não existe “tempo negativo”, então, por eliminação, o outro valor (podendo ser distância percorrida ou velocidade, por exemplo) é quem tornará a fração negativa.
Frações com denominadores diferentes:
Caso os denominadores das frações forem diferentes, precisaremos deixá-los iguais, para só então realizarmos as operações
Método do MMC: Podemos utilizar o MMC ao nosso favor, deixaremos os denominadores das frações que estiverem sendo somadas ou subtraídas seguindo o passo a passo abaixo.
Exemplo:
Resolva a operação abaixo
$$\frac{2}{3}+\frac{1}{2}$$
As frações têm denominadores diferentes, portanto, temos que deixá-los. Primeiramente, achamos o MMC dos denominadores $3$ e $2$(caso não saibas achar o MMC entre números, tem artigo aqui no blog sobre esse assunto), que é $6$, esse será o novo denominador das frações
$$\frac{?}{6}+\frac{?}{6}$$
Agora precisamos descobrir os novos numeradores, para isso, dividimos o $6$ pelos denominadores antigos e multiplicamos pelos respectivos numeradores, os resultados disso serão os novos numeradores
$$\frac{6\div3\times2}{6}+\frac{6\div2\times1}{6}=\frac{4}{6}+\frac{3}{6}$$
Então, somamos normalmente as frações com os denominadores iguais
$$\frac{4}{6}+\frac{3}{6}=\frac{4+3}{6}=\frac{7}{6}$$
Uma dica: A fração representa uma divisão, no entanto, não precisas realizar a operação de divisão, podes deixar a resposta na forma de fração, não precisas dividir o numerador pelo denominador (faça isso somente se a divisão for exata ou se seu professor pedir), podes deixar do jeito que está, pois afinal, uma fração é um número.
Método da borboleta: Carinhosamente apelidado de “método da borboleta”, há uma forma bem mais rápida e prática de somar ou subtrair duas frações, utilizarei o exemplo anterior para explicá-lo
Exemplo 1:
Resolva a operação abaixo
$$\frac{2}{3}+\frac{1}{2}$$
Para obtermos o novo denominador, multiplicamos os denominadores
$$\frac{?}{3\times2}+\frac{?}{3\times2}=\frac{?}{6}+\frac{?}{6}$$
Agora, multiplicamos o numerador da primeira fração, pelo denominador da outra e fazemos o mesmo com a segunda fração
$$\frac{2\times2}{6}+\frac{1\times3}{6}=\frac{4}{6}+\frac{3}{6}$$
E então somamos as frações
$$\frac{4}{6}+\frac{3}{6}=\frac{7}{6}$$
Parece confuso, mas podes interpretar da seguinte forma o processo que fizemos: “Multiplicamos em cruz e multiplicamos em baixo”, como ilustrado na figura abaixo:
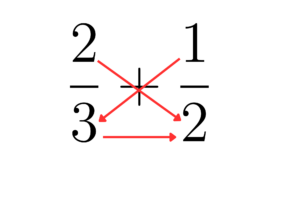
Poderíamos omitir um dos passos da resolução, pois de todo jeito iremos juntar as frações na hora de somarmos, portanto, poderíamos ter escrito assim:
$$\frac{2}{3}+\frac{1}{2}=\frac{2\times2+1\times3}{2\times3}=\frac{4+3}{6}=\frac{7}{6}$$
Exemplo 2:
Resolva a operação abaixo
$$\frac{-7}{2}+\frac{5}{4}$$
Vamos utilizar o método da borboleta, multiplicamos em cruz e multiplicamos em baixo e depois resolvemos as operações restantes
$$\frac{-7}{2}+\frac{5}{4}=\frac{-7\times4+5\times2}{2\times4}=\frac{-28+10}{8}=\frac{-18}{8}$$
Importante destacar que o método da borboleta só pode ser executado com duas frações, caso haja três ou mais frações, é mais prático utilizar o MMC, mas caso queira esse usar o método que acabamos de ver, tens que aplicar de duas em duas frações.
Multiplicação de frações:
O produto entre frações é muito tranquilo, basta multiplicamos numerador com numerador e denominador com denominador, ou seja, multiplicamos os números de cima e multiplicamos os números de baixo
Exemplo 1:
Resolva a operação abaixo
$$\frac{-2}{3}\times\frac{-6}{5}$$
Aqui tanto faz se os numeradores são iguais ou diferentes, o processo será o mesmo, multiplicamos os numeradores e denominadores entre si
$$\frac{-2}{3}\times\frac{-6}{5}=\frac{-2\times(-6)}{3\times5}$$
Sempre se lembre de realizar o “jogo de sinais”, para que não erre multiplicações envolvendo números negativos
$$\frac{-2\times(-6)}{3\times5}=\frac{12}{15}$$
Exemplo 2:
Resolva a operação abaixo
$$\frac{1}{2}\times2$$
Temos uma fração multiplicando um número inteiro, o que fazer? Todo número inteiro pode ser escrito na forma de fração, pois se dividirmos um número por $1$, nada será alterado, então, podemos reescrever o $2$ como sendo $2$ sobre $1$
$$\frac{1}{2}\times2=\frac{1}{2}\times\frac{2}{1}$$
Agora realizarmos a multiplicação
$$\frac{1}{2}\times\frac{2}{1}=\frac{1\times2}{2\times1}=\frac{2}{2}=1$$
Divisão de frações:
Quando tivermos uma fração dividida por outra, basta repetimos a primeira fração e multiplicamos pelo inverso da segunda. Inverter uma fração é trocar o numerador com o denominador.
Exemplo 1:
Resolva a operação abaixo
$$\frac{\frac{3}{7}}{\frac{2}{6}}$$
Repetimos a primeira fração e multiplicamos pelo inverso da segunda
$$\frac{\frac{3}{7}}{\frac{2}{6}}=\frac{3}{7}\times\frac{6}{2}$$
E por fim, realizamos a multiplicação de frações
$$\frac{3}{7}\times\frac{6}{2}=\frac{18}{14}$$
A divisão das frações também poderia estar representada assim (apesar de não mudar nada, pode ser útil saber):
$$\frac{3}{7}\div\frac{2}{6}$$
Exemplo 2:
Resolva a operação abaixo
$$\frac{2}{\frac{5}{3}}$$
Quando tivermos um número inteiro dividido por uma fração (ou o contrário), basta reescrevê-lo na forma de fração e realizar o processo que acabamos de utilizar
$$\frac{2}{\frac{5}{3}}=\frac{\frac{2}{1}}{\frac{5}{3}}=\frac{2}{1}\times\frac{3}{5}=\frac{6}{5}$$
Simplificação de frações
Em algum momento você irá escutar a frase “deixe a fração em sua forma irredutível”, isso significa que você terá que simplificar a sua fração ao máximo, até não poder mais. Mas afinal, o que significa simplificar uma fração? Basicamente, se resume em você dividir numerador e denominador por um determinado número (diferente de $1$), mas para isso, ambos devem ser divisíveis por esse número.
Exemplo:
Deixe a fração abaixo em sua forma irredutível
$$\frac{16}{32}$$
Tanto o numerador, quanto o denominador são pares, portanto, podemos dividi-los por $2$
$$\frac{16\div2}{32\div2}=\frac{8}{16}$$
O $8$ e o $16$ são divisíveis por $8$, então, podemos simplificar ainda mais
$$\frac{8\div8}{16\div8}=\frac{1}{2}$$
Não há um número diferente de $1$ que divida $1$ e $2$, então, a fração chegou em sua forma irredutível. É importante mencionar que caso tivéssemos o inverso dessa fração, ou seja, $2$ sobre $1$, poderíamos simplificar um pouco mais, pois $2$ dividido por $1$ é $2$.
Com a prática, você irá perceber melhor os números pelos quais você pode dividir numerador e denominador, nessa questão que resolvemos agora, tanto o $16$, quanto o $32$ são divisíveis por $16$
$$\frac{16}{32}=\frac{16\div16}{32\div16}=\frac{1}{2}$$
Separação de frações
Da mesma forma que podemos juntar duas frações com numeradores iguais, podemos separar uma fração em duas ou mais frações com o mesmo denominador.
Exemplo:
$$\frac{7}{4}=\frac{4+3}{4}=\frac{4}{4}+\frac{3}{4}=1+\frac{3}{4}$$
Tipos de frações
É interessante sabermos os tipos de classificação para as frações, pois determinados métodos como a “integração de funções racionais pelo método das frações parciais” (assunto visto em cálculo, matéria de ensino superior), será necessário identificarmos o tipo da fração.
Frações próprias:
Frações que possuem denominador maior que o numerador.
Exemplo:
$$\frac{2}{5}$$
Frações impróprias:
Frações que possuem numerador maior que o denominador.
Exemplo:
$$\frac{8}{3}$$
Frações aparentes:
Frações cuja divisão entre o numerador e o denominador resulta em um número inteiro.
Exemplo:
$$\frac{6}{3}=2$$
Frações irredutíveis:
Frações que não podem ser simplificadas.
Exemplo:
$$\frac{4}{7}$$
Frações mistas:
Frações impróprias que são reescritas como um número inteiro mais (ou menos) uma fração própria
Exemplo:
$$\frac{7}{4}=1+\frac{3}{4}$$
Frações equivalentes:
Frações que possuem o mesmo valor numérico, mesmo que seus numeradores e denominadores sejam diferentes
Exemplo:
$$\frac{20}{10}=2$$
$$\frac{10}{5}=2$$
As frações acima são aparentes, pois ambas valem $2$, e seus numeradores e denominadores são diferentes.
Exercícios resolvidos de frações
1. Resolva as operações abaixo e escreva a resposta na forma irredutível
$$\frac{1}{3}+\frac{4}{3}-\frac{5}{6}$$
Podemos resolver de duas formas, pelo método do MMC ou método da borboleta, como são três frações, o primeiro método é mais rápido, mas irei resolver dos dois jeitos
Método do MMC:
Tiramos o MMC, ele será o novo denominador e então, dividimos ele pelos denominadores e multiplicamos pelos numeradores
$$\frac{1}{3}+\frac{4}{3}-\frac{5}{6}=\frac{6\div3\times1+6\div3\times4-6\div6\times5}{6}$$
Efetuamos então as operações
$$\frac{6\div3\times1+6\div3\times4-6\div6\times5}{6}=\frac{2+8-5}{6}=\frac{5}{6}$$
Podíamos ter somado as duas frações com denominadores iguais, mas isso não impactaria no resultado. Ela já está em sua forma irredutível, portanto, paramos por aqui o cálculo. Uma grande vantagem desse método é que a fração resultante, ao final dos cálculos, estará na sua forma irredutível.
Método da borboleta:
Primeiro, vamos somar as frações com o mesmo denominador
$$\frac{1}{3}+\frac{4}{3}-\frac{5}{6}=\frac{1+4}{3}-\frac{5}{6}=\frac{5}{3}-\frac{5}{6}$$
Agora, “multiplicamos em cruz e multiplicamos em baixo”
$$\frac{5}{3}-\frac{5}{6}=\frac{5\times6-3\times5}{3\times6}=\frac{30-15}{18}=\frac{15}{18}$$
Podemos simplificar numerador e denominador por $3$
$$\frac{15}{18}=\frac{15\div3}{18\div3}=\frac{5}{6}$$
Chegamos enfim, na forma irredutível.
2. Resolva as operações abaixo e escreva a resposta na forma irredutível
$$\frac{\frac{3}{2}}{\frac{1}{5}}\times\frac{1}{3}$$
Apesar de parecer algo complicado, não faremos nada que já não tenhamos realizado nesse artigo. Começamos reescrevendo as frações divididas como um produto entre uma vezes o inverso da outra
$$\frac{\frac{3}{2}}{\frac{1}{5}}\times\frac{1}{2}=\frac{3}{2}\times\frac{5}{1}\times\frac{1}{3}$$
Multiplicamos então, todos os numeradores e denominadores entre si
$$\frac{3}{2}\times\frac{5}{1}\times\frac{1}{3}=\frac{3\times5\times1}{2\times1\times3}=\frac{15}{6}$$
Ainda não acabamos, pois o $15$ e o $6$ são divisíveis por $3$
$$\frac{15}{6}=\frac{15\div3}{6\div3}=\frac{5}{2}$$
Importância de aprender frações
O conhecimento sobre frações só não é mais importante do que saber as quatro operações básicas da matemática, mas além de ser inúmeras vezes mais prático trabalhar com frações do que com números decimais, elas aparecem em praticamente todos os assuntos da matemática, então ao invés de tentar fugir quando encontrares frações no meio dos cálculos, se tornar amigo delas irá lhe trazer inúmeras vantagens e lhe poupar muita dor de cabeça.
