A análise ou como é chamado por muitos, jogo de sinais, é um conceito fundamental na matemática que ajuda a realizar operações básicas como adição, subtração, multiplicação e divisão com números inteiros. Ela define como os sinais dos números (
O que são sinais na matemática?
O sinal de um número indica se ele é positivo ou negativo. Os números positivos aqueles que são maiores que zero, e são indicados com um sinal de mais (
Exemplos:
1)
2)
3)
Já os números negativos, são valores menores que zero e são indicados com um sinal de menos (
Exemplos:
1)
2)
3)
Apesar dos símbolos serem os mesmos utilizados na soma e subtração, eles representam coisas diferentes em cada assunto. E onde o zero entra nessa história? Ele é considerado um número neutro, que nem é positivo, nem é negativo.
Valor absoluto de um número:
O valor absoluto de um número, também chamado magnitude, é o número sem considerar seu sinal. Por exemplo, o valor absoluto tanto de
Regra de sinais na adição e subtração:
Na adição, os procedimentos variam dependendo se os sinais dos números envolvidos são iguais ou diferentes.
Sinais iguais: Ao somar números com o mesmo sinal, basta somar os valores absolutos e manter o sinal que eles possuem. Por exemplo:
Sinais diferentes: Para somar números com sinais opostos, subtraia o menor valor absoluto do maior e mantenha o sinal do número com maior valor absoluto. Por exemplo:
Exemplo:
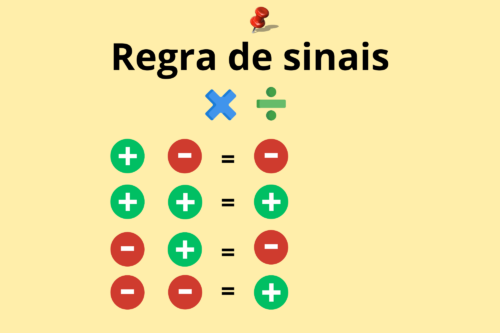
Regra de sinais na multiplicação e divisão:
Ao multiplicar dois números com sinais iguais o resultado será um número positivo.
Exemplos:
1)
2)
Por outro lado, quando os números têm sinais diferentes, o produto é um número negativo.
Exemplos:
1)
2)
Para a divisão, a regra de sinais segue o mesmo princípio da multiplicação. Dividir números com sinais iguais, resultará em um número positivo:
Exemplos:
1)
2)
E se divirmos números com sinais diferentes, o resultado será negativo:
Exemplos:
1)
2)
Como interpretar os sinais dos numéricos?
Na prática, o que significa um número positivo e um número negativo? Podemos usar a analogia de uma conta bancária, os números negativos representam déficits (como uma dívida) e positivos representam excedentes (como saldo disponível).
Se tivermos uma dívida no banco de
Se ao invés de depositarmos
Outra aplicação cujo sinal do número tem um significado para além dos cálculos matemáticos é a temperatura.
Exercícios resolvidos de regra de sinais
1. Calcule o valor de
Primeiro, vamos somar o
Em seguida, faremos o mesmo
2. Encontre o produto de
Temos uma multiplicação de dois números com sinais iguais, portanto, o resultado será positivo
3. Qual é o quociente de
Agora temos um número negativo dividido por um positivo, o resultado será negativo:
4. Qual é o resultado da expressão
Temos três números se multiplicando, como realizar a análise? Da esquerda para a direita, efetuamos as multiplicações e analisamos os sinais de dois em dois números. Primeiro, temos a multiplicação de dois números com mesmo sinal, então o resultado será positivo
Por fim, temos dois números com sinais diferentes se multiplicando, e o resultado terá sinal negativo
Importância de aprender a regra de sinais
A aplicação correta dessas regras é essencial, repito, essencial, pois caso a análise seja feita de forma errada, todo o resto do cálculo, inclusive a resultado, estará errado.
Formado em Eletrotécnica pelo IFRN, além de ter cursos de Matemática Básica e Cálculo pela empresa Help Engenharia.
