Muito presente em alguns tipos de equações, como as de $1°$ e $2°$ graus, faz com que entender o que são os polinômios e como trabalhar com eles seja essencial para que não haja complicação em várias manipulações matemáticas.
O que é polinômio?
Simplificadamente, um polinômio é uma expressão matemática que contém números e letras que se multiplicam e são somadas ou subtraídas.
Exemplos de polinômios:
1) $x^2-2x+1$
2) $x^5+2x^3+5x^2$
3) $-3x^3-9$
Diferentemente de uma expressão genérica, nos polinômios não há termos que possuam a variável em seus elementos, deves ter ficado confuso com essa afirmação, mas me refiro a termos como $sen(x)$, $\log_{2}x$ e $3^x$, cuja letra não é o ponto central, e ela está presente em lugares “secundários”, como no argumento do seno, logaritmando do log ou no expoente. De forma geral, um polinômio possui a seguinte aparência:
$$ax^n+bx^{n-1}+…+cx^2+dx^1+e$$
Sendo as letras $a$, $b$, $c$ números quaisquer, chamados de coeficientes, e a variável (letra) se repetindo com expoentes diferentes, esses últimos representados por $n$, $n-1$, e assim por diante. Mas não se assuste com esse tanto de letra, pois o que precisas entender é que um polinômio possui partes numéricas (coeficientes) e partes literais (variáveis). Uma informação importante é que só são permitidos expoentes positivos na(s) variável(eis), portanto, se houver uma letra com expoente negativo, a expressão não será considerada um polinômio, mesmo que as demais características indiquem o contrário.
Casos importantes de polinômios
Existem casos específicos de polinômios que são geralmente enfatizados em aulas pelo mundo à fora, pois há aplicações na matemática para eles, sendo eles o monômio, o binômio e o trinômio.
Monômio:
Um monômio, é um polinômio que possui apenas um termo, tendo então, um único coeficiente e variável.
Exemplos de monômios:
1) $x^3$
2) $20x^2$
3) $-6y$
Nas salas de aulas e em muitos artigos, os polinômios são descritos como somas (ou subtrações) de dois ou mais monômios, isso não é totalmente verdade, o próprio monômio, por definição, é um polinômio, mas essa ideia é complexa e até impossível de se compreender para muitos estudantes, pois o prefixo “poli” dá ideia de mais de uma coisa, então como algo que tem o prefixo “mono”, cujo sentido é de algo único, pode ser também um polinômio? Por esse motivo é utilizada essa explicação, não culpem os professores, eles estão tentando ser didáticos, porque a nível de ensino médio e até de graduações que não são licenciaturas, não é necessário saber a definição exata de polinômio, que convenhamos, é bem confusa.
Binômio:
Basicamente, um binômio é um polinômio que tem apenas dois termos, em outras palavras, dois momômios.
Exemplos de binômios:
1) $x^2-4$
2) $-x^3-y^2$
3) $-2x^2+7x$
Uma aplicação para esse tipo de polinômio muito conhecida e utilizada é o “binômio de Newton”, que consiste em uma tabela com o resultado de binômios elevados a expoentes quaisquer, partindo do zero.
Exemplos de binômios de Newton:
1) $(a+b)^2$
2) $(2x-4)^3$
3) $(y+4x)^0$
Trinômio:
Por sua vez, um trinômio, como o próprio nome sugere, é um polinômio que contém três termos.
Exemplos de trinômios:
1) $x^2+4x+4$
2) $x^2+y^2+z^2$
3) $x^2+yx^3-10$
Já deves ter se deparado com esse nome, pois um dos métodos de fatoração é chamado trinômio quadrado perfeito, sendo um trinômio que tem dois dos termos sendo quadrados perfeitos (cuja raiz quadrada é exata), e ao multiplicarmos as raízes desses dois termos e multiplicarmos eles entre si e por $2$ ou $-2$, chegamos no terceiro.
Exemplos de trinômios quadrados perfeitos:
1) $x^2-6x+9$
2) $x^6+2x^3y^2+y^4$
3) $\frac{9a^2}{4b^4}+\frac{ay}{48b^2}+\frac{y^2}{36}$
Grau de um polinômio
Para definir o grau de um polinômio, basta identificarmos qual é o maior expoente que eleva a variável, ou seja, qual é o expoente com maior valor entre as partes literais do polinômio.
Exemplo:
Classifique os polinômios abaixo quanto aos seus graus
a) $x^5+x^3-x-3$
b) $x^2-y^4-2^6$
c) $y^5-x^3y^3+x^2y$
a) Resposta:
Na letra $a$, temos um polinômio de grau $5$, pois o maior expoente da variável $x$ é $5$.
b) Resposta:
Já na sentença $b$ temos duas letras, mas o processo é o mesmo, olhemos para a que tem maior expoente, que é o $y^4$, portanto, o polinômio é de quarto grau (grau $4$). Podes se perguntar, mas e o $2^6$? Ele não possui o maior expoente?
Como disse anteriormente, somente a parte literal é importante ao definirmos o grau de um polinômio.
c) Resposta:
Por fim, na $c$ há termos com uma letra, e agora? Quando temos essa situação, somamos os expoentes de todas as letras de cada termo, o maior número definirá o grau do polinômio.
Primeiro termo:
$y^5$, grau $5$
Segundo termo:
$-x^3y^3$, grau $6$, pois $3+3=6$
Terceiro termo:
$x^2y$, grau $3$, pois $2+1=3$
Nosso polinômio é de grau $6$ (sexto grau), como podemos concluir com os cálculos acima.
No caso de monômios, como só há um termo, o grau vai ser igual ao expoente da única letra que houver, mas caso haja mais de uma letra no monômio, o grau dele vai ser a soma dos expoentes delas.
Operações com polinômios
Assim como podemos operacionalizar números, é possível somar, subtrair e até mesmo fatorar um polinômio, como veremos a seguir.
Soma e subtração de polinômios:
Ao somarmos ou subtrairmos polinômios, devemos juntar os termos semelhantes, ou seja, que possuem a parte literal igual, e ao fazermos isso, somaremos ou subtrairemos seus coeficientes (parte numérica) e manteremos a parte literal. E em relação aos números que não possuem variável, basta somá-los (ou subtraí-los).
Exemplo:
Some os polinômios $x^2-xy+4$ e $3x^2+xy-2$
Primeiramente, vamos montar a expressão matemática com os polinômios
$$x^2-xy+4+(3x^2+xy-2)$$
É importantíssimo colocarmos os parênteses para que não haja erro por causa dos sinais, nesse caso, como o sinal é de soma, nada mudará nos sinais do polinômio dentro dos parênteses.
$$x^2-xy+4+3x^2+xy-2$$
Agora, vamos deixar os termos semelhantes lado a lado para facilitar a visualização
$$x^2+3x^2-xy+xy+4-2$$
Por fim, operacionalizamos os termos semelhantes
$$x^2+3x^2-xy+xy+4-2$$
$$(1+3)x^2+(1-1)xy+2$$
$$4x^2+0xy+2$$
$$4x^2+2$$
Multiplicação de polinômios:
Para multiplicar polinômios, aplicamos a boa e velha propriedade distributiva, multiplicado cada termo de um polinômio por todos os termos do outro, e então juntamos os termos semelhantes, caso haja.
Exemplo:
Calcule a multiplicação entre os polinômios $x^2-3$ e $x+y^2+1$
Montamos a expressão matemática indicando a multiplicação a ser feita
$$(x^2-3).(x+y^2+1)$$
Agora aplicamos a propriedade distributiva, para facilitar a visualização, irei organizar bem passo a passo:
$$(x^2-3).(x+y^2+1)$$
$$x^2.(x+y^2+1)-3.(x+y^2+1)$$
$$x^2.x+x^2.y^2+x^2.1-3.x-3.y^2-3.1$$
$$x^3+x^2y^2+x^2-3x-3y^2-3$$
Não há termos semelhantes, então, paramos o cálculo por aqui.
Divisão de polinômios:
A divisão de polinômios é a mais trabalhosa e difícil das operações, pois temos que ter muito cuidado nos cálculos e seguir um processo bem definido.
Exemplo:
Divida o polinômio $-2x^2+4x-2$ pelo polinômio $x-1$
Primeiramente, colocamos divisor e dividendo (quem será dividido e quem divide), da seguinte forma:
Então, colocaremos no dividendo um termo que multiplicado pelo divisor, resulte no termo de maior grau do polinômio que está sendo dividido. Em seguida, multiplicamos ele por todos os termos do polinômio divisor
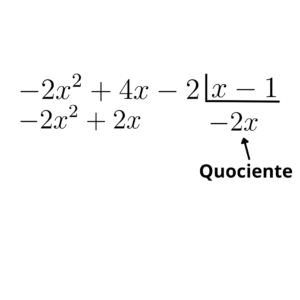
E agora subtraímos os polinômios
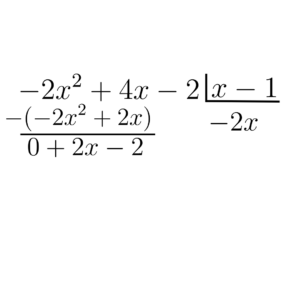
Repetimos o processo até que o resto da divisão tenha grau menor que o grau do polinômio que está dividindo, nesse caso o $x-1$
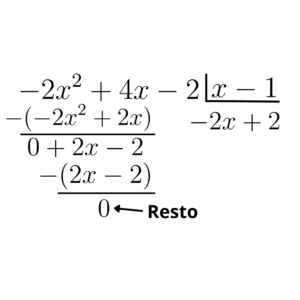
É meio complicado no começo, mas não é comum dividirmos polinômios no ensino médio, sendo bem mais útil no ensino superior, mas caso queira verificar se acertou a divisão, basta multiplicar o dividendo pelo divisor e somar com o resto, se o resultado bater com o polinômio que foi dividido, a resposta está certa.
$$(-2x+2).(x-1)+0=-2x^2+2x+2x-2=-2x^2+4x-2$$
Fatoração de polinômios
Há um processo que não necessariamente é uma operação, mas que aparece muito em exercícios que precisamos simplificar expressões algébricas, que é a fatoração, especificamente fatoração de polinômios, que consiste em transformarmos termos que estão sendo somados ou subtraídos em termos se multiplicando, ou seja, transformar somas e subtrações em multiplicação, isso nos permite simplificar uma expressão com a finalidade de deixá-la menor. Só mencionarei a existência desse processo e não irei o explicar, pois tem artigo sobre esse assunto aqui no blog, onde explico passo a passo como fatorar, não deixe de lê-lo para se inteirar sobre esse importante dispositivo.
Polinômios completos e incompletos
Simplificadamente, polinômios completos são aqueles que possuem termos com todos os graus menores que o maior grau, em outras palavras, se um polinômio tem grau $3$, ele será considerado completo caso tenha termos com grau $2$, $1$ e $0$ (a constante), e caso falte um deles, o polinômio é classificado como incompleto.
Exemplos de polinômios completos:
1) $y^3-2y^2+y-5$
2) $7x^4+x^3-2x^2-x+3$
3) $x-5$
Exemplos de polinômios incompletos:
1) $x^3+2$
2) $-9x^5+x^2$
3) $x^3-x+1$
Exercícios resolvidos de polinômios
1. Classifique em monômio, binômio e trinômio os polinômios abaixo
a) $x^2-y^3$
b) $x^2+9$
c) $g^4$
d) $-3+x-x^2$
Resolução:
Os dois primeiros são binômios, pois possuem dois termos, já o terceiro é um monômio, possuindo apenas $g^4$ como único termo e por fim, o $-3+x-x^2$ é um trinômio, uma vez que há três termos nele.
2. Determine o grau dos polinômios abaixo
a) $-y^2+x-2+y^3$
b) $x^7+8x$
c) $y^2-x^4+3^5$
d) $x^3y^2-y^4+6$
Respostas:
a)
Na letra $a$ temos um polinômio de grau $3$, pois apesar do termo de terceiro grau não estar mais a esquerda na expressão, ele não deixa de ser o com maior grau.
b)
Na $b$ temos um polinômio de sétimo grau, não se iluda com o coeficiente $8$, ele não é um expoente, portanto, não deve ser considerado na análise.
c)
O polinômio da letra $c$ tem grau $4$, apesar do $3$ estar elevado à $5$, o que nos interessa é a parte literal, pois o expoente dela é que definirá o grau do polinômio.
d)
E por fim, termos um polinômio de quinto grau, podemos ser induzidos a achar que o $y^4$ detêm o maior grau, mas não poderíamos estar mais enganados caso achássemos isso, porque como há um termo com duas letras distintas, é necessário somar seus expoentes para sabermos o grau do termo como um todo, e $2+3=5$, que é maior que o $4$ do $y^4$.
3. Calcule o perímetro do retângulo:
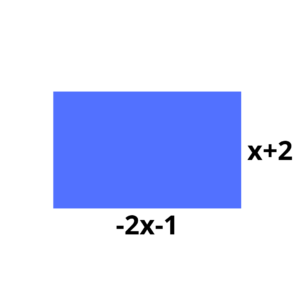
Resolução:
Essa questão necessita de um conhecimento básico sobre geometria. Para calcular o perímetro de qualquer figura geométrica, precisamos apenas somar o comprimento de todos os lados da figura, então, se tivéssemos um quadrado de lados medindo $3$, para calcular seu perímetro seria necessário somar quatro vezes $3$, que resultaria em $12$. No exercício acima, temos um retângulo, cujos lados opostos são iguais (na verdade são os lados paralelos, mas para simplificar utilizarei opostos), então, podemos redesenhar ele da seguinte forma:
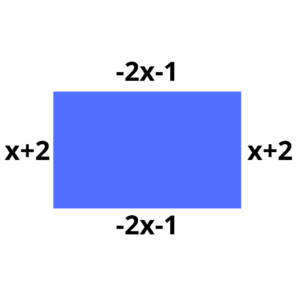
Agora podemos calcular seu perímetro, somando todos os seus lados
$$x+2+(-2x-1)+(x+2)+(-2x-1)=x+2-2x-1+x+2-2x-1$$
$$x+2-2x-1+x+2-2x-1=-2x+2$$
4. Calcular $m$ para que o polinômio $(2m-4)x^2+x-2$ tenha grau $1$
Resolução:
Para que um polinômio possua determinado grau, o maior expoente dele deve ter o mesmo valor do grau, ou seja, se o grau é $2$ o maior expoente tem de ser $2$ e assim por diante. Então, para que o polinômio acima tenha grau $1$, o coeficiente que multiplica $x^2$ deve ser zero, para que ao multiplicá-los o $x^2$ “suma” da expressão, sobrando apenas o $x$, fazendo com que o polinômio tenha grau $1$. Para descobrir o valor de $m$, igualaremos o coeficiente $2m-4$ à $0$
$$2m-4=0$$
Por fim, isolamos o $m$ para resolver a equação
$$2m-4=0$$
$$2m=4$$
$$m=\frac{4}{2}$$
$$m=2$$
Vamos substituir esse valor no polinômio para verificarmos se alcançamos nosso objetivo
$$(2m-4)x^2+x-2$$
$$(2.2-4)x^2+x-2$$
$$(4-4)x^2+x-2$$
$$0x^2+x-2$$
$$x-2$$
Formado em Eletrotécnica pelo IFRN, além de ter cursos de Matemática Básica e Cálculo pela empresa Help Engenharia.
