Ângulo, um conceito que atravessou séculos e é muito utilizado nas mais diversas áreas do conhecimento matemático e científico, pode ser nosso maior aliado em questões de física e até mesmo em análises de circuitos elétricos.
O que é um ângulo?
Em poucas palavras, o ângulo pode ser definido como a medida que representa quão abertas duas semirretas (pedaço de uma reta, possui um tamanho limitado), que possuem mesma origem, estão em relação a elas mesmas. Ou seja, ele indica a abertura entre duas semirretas que partem de um mesmo ponto. Utilizamos uma letra grega para nomear um ângulo genérico e um símbolo circular que vai de uma semirreta a outra.
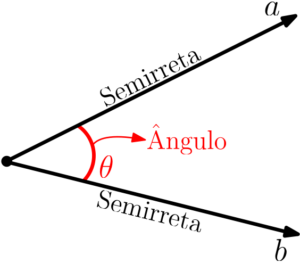
Unidades de medida do ângulo
Utilizamos duas unidades de medida para o ângulo, graus e radianos. Para termos uma referência, utilizando como base uma circunferência, por conversão, a dividimos em
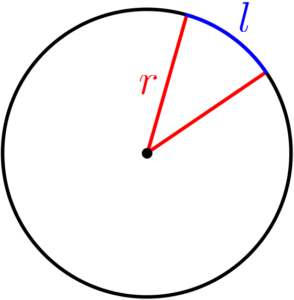
Formaremos assim, um arco de circunferência entre elas. O comprimento do arco (
Com essa informação, vamos descobrir quanto equivale um grau em radianos.
Se quisermos converter de graus para radianos, basta multiplicarmos o valor em graus por
Caso queira de onde surgiu o conceito de ângulo e o por que a circunferência foi dividida em
Tipos de ângulos
Há alguns ângulos importantes, que são comumente encontrados nos mais diversos exercícios que envolvem esse assunto, e cada um possui um nome próprio.
Ângulo reto:
É o nome dado a o ângulo de
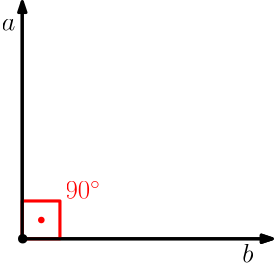
Em radianos, noventa graus equivalem à
Ângulo raso:
Quem detém esse nome é o ângulo de
Em radianos, cento e oitenta graus equivalem à
Ângulo volta completa ou nulo:
Já mencionado anteriormente, o ângulo volta completa é o de
Nessa mesma situação, podemos dizer que a abertura entre as semirretas é nula, uma vez que elas não possuem abertura entre si.
Classificação dos ângulos
Podemos classificar um ângulo de acordo com seu valor, e sua relação com outro(s) ângulo(s).
Ângulo agudo:
Um ângulo é considerado agudo quando mede menos que
Ângulo obtuso:
Para ser considerado obtuso o ângulo deve ser maior que
Ângulos complementares:
Dois ou mais ângulos são definidos como complementares, quando juntos formam
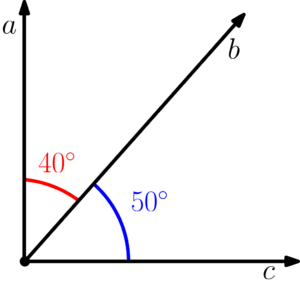
Na imagem acima, dizemos que o ângulo de
Ângulos suplementares:
Dois ou mais ângulos são suplementares se ao somá-los o resultado seja
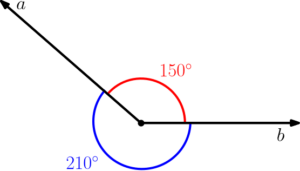
Ângulos replementares:
Ângulos replementares são aqueles que geram um ângulo de
Ângulos congruentes:
Dizemos que dois ângulos são congruentes quando eles possuem o mesmo valor, ou seja, quando são iguais. E isso vale independentemente da unidade de medida utilizada; então, se temos um ângulo alfa valendo
Ângulos notáveis
Existem três ângulos que são muito importantes no estudo da trigonometria e da geometria, eles são chamados de ângulos notáveis, e medem, respectivamente,
Ângulo de
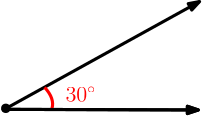
Em radianos, trinta graus equivalem à
Ângulo de
Em radianos, quarenta e cinco graus equivalem à
Ângulo de
Em radianos, trinta graus equivalem à
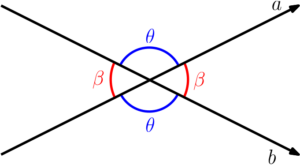
Ângulos opostos pelo vértice
Há um conceito envolvendo ângulos que é muito útil e pode ser utilizado em vários contextos. Ângulos que são opostos em relação a um vértice (ponto de intersecção entre semirretas, nesse caso), são iguais, como podemos visualizar na figura abaixo.
Formado em Eletrotécnica pelo IFRN, além de ter cursos de Matemática Básica e Cálculo pela empresa Help Engenharia.
